Teoria
A parte teórica da Ajuda contém todas as bases teóricas utilizadas nas computações realizadas pelos programas GEO5.
Tensões no Subsolo
O nosso software calcula as tensões nos solos conforme descrito nos seguintes capítulos:
- Tensões geostáticas no subsolo, computação de empuxos
- Tensão efetiva / total
- Aumento de tensões devido a sobrecargas
- Aumento de tensões sob sapatas
Tensões Geostáticas no Subsolo, Computação de Empuxos
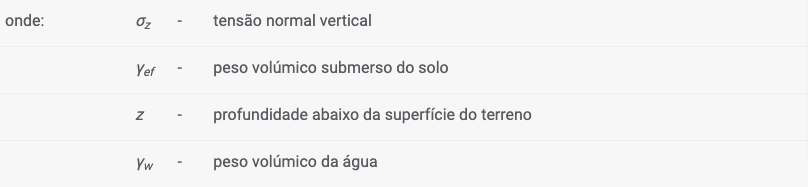
A análise de tensões baseia-se na existência de camadas de solos, definidas pelo usuário durante a introdução de dados. O programa também adiciona camadas fictícias nas zonas em que as tensões e pressões laterais (nível freático, pontos de construção, etc.) sofrem alterações. A tensão normal na iésima camada é computada de acordo com:
![]()

Se a camada se encontrar abaixo do nível freático, o peso volúmico do solo abaixo do nível freático é definido através dos parâmetros do solo introduzidos, da seguinte forma:
![]() para a opção “Padrão“:
para a opção “Padrão“:
![]()

![]() para a opção “Calcular a partir da porosidade“:
para a opção “Calcular a partir da porosidade“:
![]()

![]()

O valor do peso volúmico da água assumido pelo programa é de 10 kN/m3 ou 0.00625 ksi.
Se a superfície do terreno atrás da estrutura for definida como inclinada (β ≠ 0) e a inclinação das camadas do subsolo com o ângulo β, ao computar o coeficiente de empuxo de terra K, este é reduzido na iésima camada, recorrendo à seguinte expressão:
![]()

Tensão Efetiva / Total
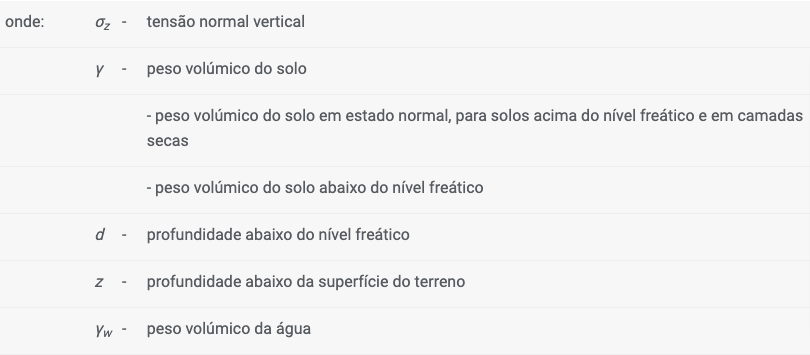
A tensão normal vertical σz é definida como:
![]()
Na sua forma geral, a expressão seguinte traduz o conceito de tensão efetiva:
![]()


O conceito da tensão efetiva só é válido para a tensão normal σ, uma vez que a tensão de cisalhamento τ não é transferida através da água de modo a ser efetiva. A tensão total é determinada através de ferramentas básicas da mecânica dos solos, sendo a tensão efetiva determinada como a diferença entre a tensão total e a pressão neutra (nos poros) (isto é, sempre através de cálculos, não pode ser medida). As pressões nos poros são determinadas a partir de testes laboratoriais ou ensaios in situ, ou a partir de cálculos. Decidir se se deve utilizar a tensão total ou efetiva não é simples. A tabela seguinte pode fornecer algumas recomendações gerais, válidas para a maioria dos casos. Deve ser tido em consideração que a tensão total depende da forma de carregamento do solo pelo seu peso próprio e efeitos externos. Enquanto que para a pressão nos poros, é assumido que para a ocorrência de fluxo de água, a pressão nos poros é uma pressão hidrodinâmica, caso contrário, é uma pressão hidrostática. Em solos parcialmente saturados, é necessário considerar que a pressão nos poros engloba a presença de água e de bolhas de ar.

Em subsolos com camadas com diferentes pesos volúmicos, a tensão normal vertical é determinada como o somatório do peso de todas as camadas acima do ponto em análise:
![]()
Aumento de Tensões devido a Sobrecargas
O aumento de tensões no subsolo ou em maciços rochosos devido a sobrecargas é computado através da teoria do subsolo elástico (Boussinesq).
O aumento da tensão num ponto no interior do subsolo ou de um maciço rochoso devido a uma sobrecarga contínua infinita é obtido da seguinte forma:
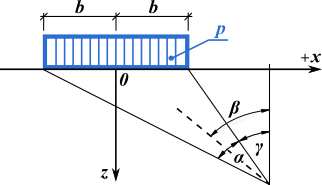
Uma sobrecarga trapezoidal é automaticamente subdividida pelo programa em dez segmentos. Cada segmento é assumido como uma sobrecarga contínua. A tensão resultante é o somatório das sobrecargas parciais.
O aumento da tensão devido a sobrecargas concentradas é computado da seguinte forma:

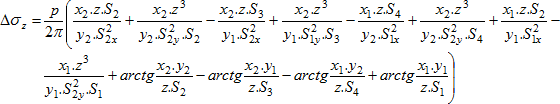
Onde:

Aumento de Tensões sob Sapatas
No programa “Sapata“, a distribuição de tensões sob a fundação é determinada a partir da combinação dos seguintes diagramas de esforços:
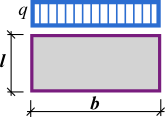
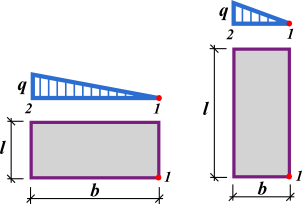
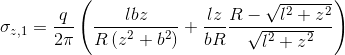
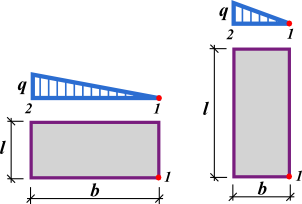
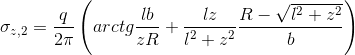
Empuxos de Terra
O software GEO5 considera as seguintes categorias de empuxos:
![]() empuxos ativos
empuxos ativos
![]() empuxos passivos
empuxos passivos
![]() empuxos em repouso
empuxos em repouso
Ao computar os empuxos, o programa permite fazer a distinção entre estados de tensão efetiva e total e estabelecer várias formas para calcular o empuxo. É, ainda, possível considerar os seguintes efeitos na magnitude do empuxo:
![]() influência de sobrecargas
influência de sobrecargas
![]() influência do nível freático
influência do nível freático
![]() influência de fendas no solo
influência de fendas no solo
![]() atrito entre o solo e a estrutura
atrito entre o solo e a estrutura
![]() aderência do solo
aderência do solo
![]() influência de cunhas no solo em consolas
influência de cunhas no solo em consolas
![]() influência sísmica
influência sísmica
A seguinte convenção é utilizada no programa, texto e expressões apresentadas.
Ao definir maciços rochosos, também é necessário introduzir a coesão da rocha c e o ângulo de atrito interno da rocha φ. Estes valores podem ser obtidos a partir de ensaios geológicos ou da tabela de valores recomendados.
Convenção
A seguinte convenção é utilizada no programa, texto e expressões apresentadas.

![]() a inclinação da superfície do terreno β é positiva no sentido anti-horário
a inclinação da superfície do terreno β é positiva no sentido anti-horário
![]() a inclinação da parede da estrutura α é positiva no sentido anti-horário
a inclinação da parede da estrutura α é positiva no sentido anti-horário
![]() o atrito entre o solo e a parede da estrutura δ é positivo se a resultante dos empuxos e a direção normal à base da estrutura formem um ângulo com sentido horário
o atrito entre o solo e a parede da estrutura δ é positivo se a resultante dos empuxos e a direção normal à base da estrutura formem um ângulo com sentido horário
Empuxo Ativo
O empuxo ativo é a menor pressão limitadora lateral desenvolvida numa falha de cisalhamento, devido ao afastamento da parade em relação ao solo, na direção do empuxo atuante (a rotação mínima da parede necessária para o desenvolvimento do empuxo ativo é cerca de 2 mrad, isto é, 2 mm/m da altura da parede).
As seguintes teorias e abordagens podem ser utilizadas para a computação de empuxos ativos, considerando estados de tensão efetiva:
![]() Teoria de Mazindrani (Rankine)
Teoria de Mazindrani (Rankine)![]() Teoria de Coulomb
Teoria de Coulomb![]() Teoria de Müller-Breslau
Teoria de Müller-Breslau![]() Teoria de Caquot
Teoria de Caquot
![]() Teoria de Absi
Teoria de Absi
![]() SP 22.13330.2016
SP 22.13330.2016
Para solos coesivos, é possível considerar a existência de cortes por tensão, isto é, o valor negativo do empuxo ativo é desenvolvido devido à coesão, ou, de acordo com requisitos mais restritos, o valor da “Menor pressão de dimensionamento” é excedido, o valor do empuxo ativo passa a ser zero ou definido como igual à “Menor pressão de dimensionamento”.
O programa também permite executar a análise para o estado de tensão total.
Empuxo Ativo – Teoria de Mazindrani (Rankine)
O empuxo ativo é dado pela seguinte expressão:
![]()


Para solos não coesivos (c = 0) com superfície do terreno horizontal (β = 0) o empuxo ativo é obtido através da solução de Rankine:
![]()
sendo o coeficiente de empuxo ativo:
![]()
As componentes horizontal e vertical do empuxo ativo são dadas por:
![]()
![]()

Bibliografia:
Mazindrani, Z.H., and Ganjali, M.H. 1997. Lateral earth pressure problem of cohesive backfill with inclined surface. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 123(2): 110-112.
Empuxo Ativo – Teoria de Coulomb
O empuxo ativo é dado pela seguinte expressão:
![]()
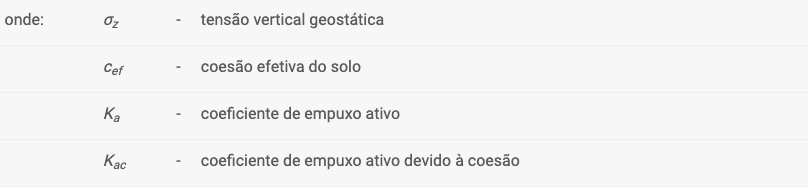
O coeficiente de empuxo ativo Ka é dado por:
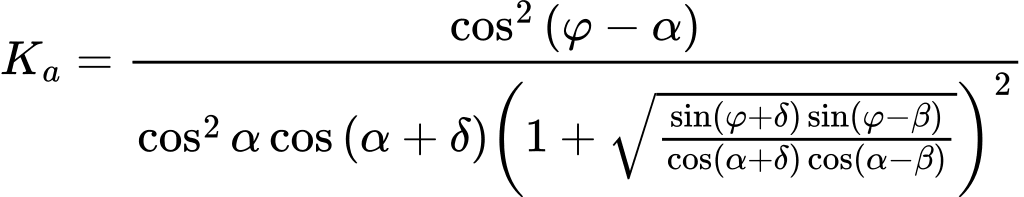
coeficiente de empuxo ativo devido à coesão Kac é dado por:
para: ![]()
![]()
![]()
para: ![]()
![]()
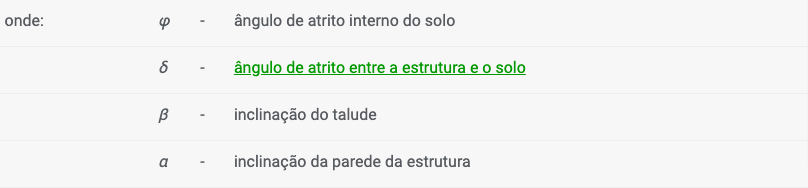
As componentes horizontal e vertical do empuxo ativo são dadas por:
![]()
![]()

Empuxo Ativo – Teoria de Müller-Breslau
O empuxo ativo é dado pela seguinte expressão:
![]()
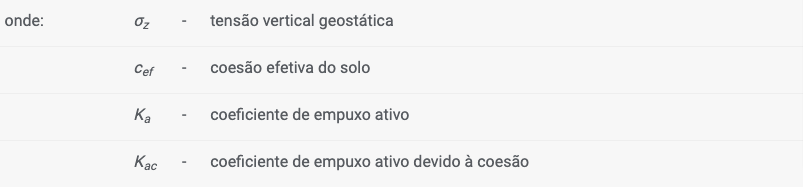
O coeficiente de empuxo ativo Ka é dado por:
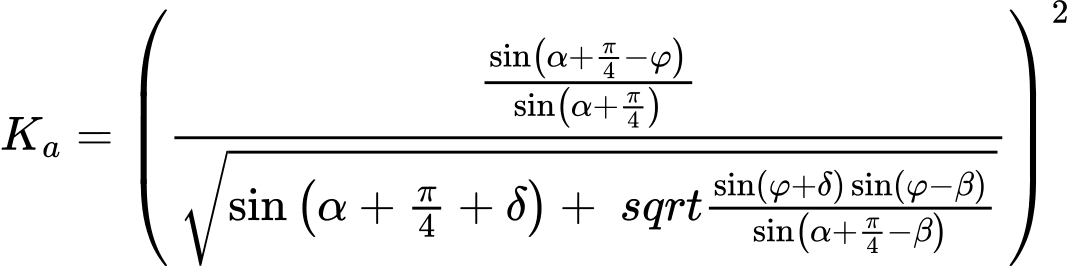
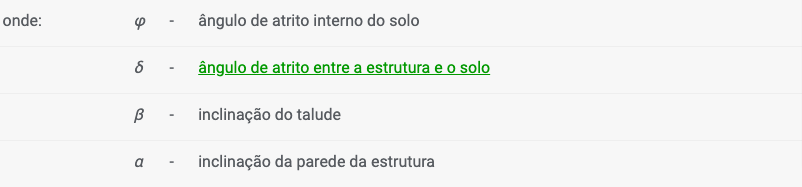
O coeficiente de empuxo ativo devido à coesão Kac é dado por:
para: ![]()
![]()
![]()
para: ![]()
![]()
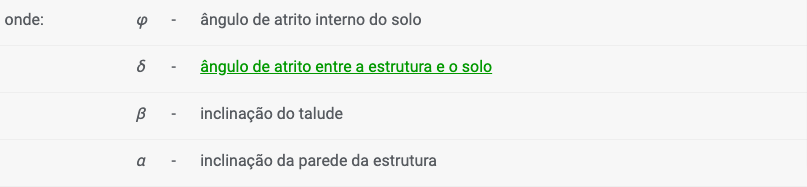
As componentes horizontal e vertical do empuxo ativo são dadas por:
![]()
![]()

Bibliografia:
Müller-Breslau’s Erddruck auf Stutzmauern,Stuttgart: Alfred Kroner-Verlag, 1906 (German).
Empuxo Ativo – Teoria de Caquot
O empuxo ativo é dado pela seguinte expressão:
![]()
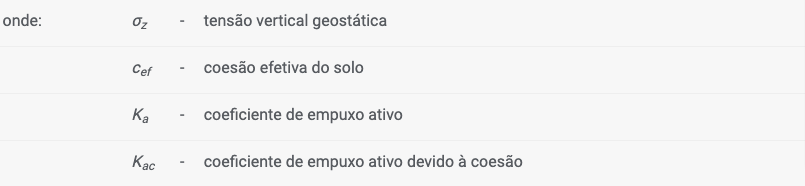
A seguinte solução analítica (Boussinesque, Caquot) é implementada para computar o coeficiente de empuxo ativo Ka:
![]()

![]()
![]()
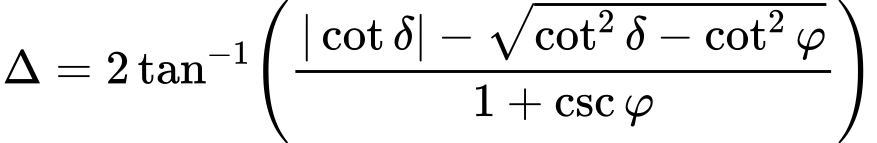
![]()

O coeficiente de empuxo ativo Kac é dado por:
for: ![]()
![]()
![]()
for: ![]()
![]()

As componentes horizontal e vertical do empuxo ativo são dadas por:
![]()
![]()

Empuxo Ativo – Teoria de Absi
O empuxo ativo é dado pela seguinte expressão:
![]()
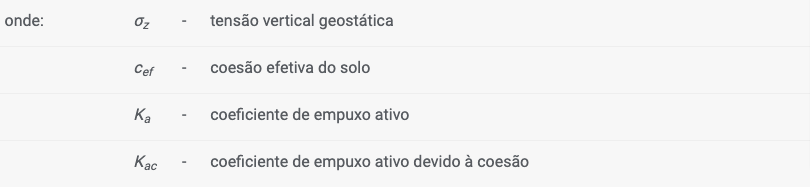
O programa admite os valores para o coeficiente de empuxo ativo Ka da base de dados, que contém os valores publicados em: Kérisel, Absi: Active and passive earth Pressure Tables, 3rd Ed. A.A. Balkema, 1990 ISBN 90 6191886 3.
O coeficiente de empuxo ativo Kac é dado por:
para: ![]()
![]()
![]()
para: ![]()
![]()
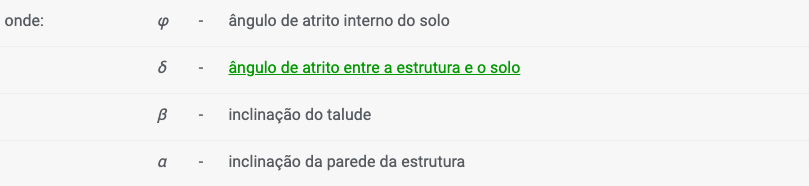
As componentes horizontal e vertical do empuxo ativo são dadas por:
![]()
![]()

Bibliografia:
Kérisel, Absi: Active and Passive Earth Pressure Tables, 3rd ed., Balkema, 1990 ISBN 90 6191886 3.
Active Earth Pressure – SP 22.13330.2016
Active earth pressure is given by the following formula:
![]()

The coefficient of active earth pressure Ka is given by:
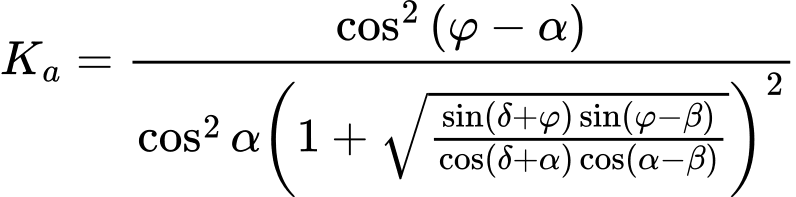

Horizontal and vertical components of the active earth pressure become:
![]()
![]()

Empuxo Ativo – Tensão Total
Para determinar o empuxo ativo em solos coesivos totalmente saturados, para os quais, normalmente, não se verifica consolidação (condições não drenadas), a tensão horizontal total σx é obtida através da seguinte expressão:
![]()
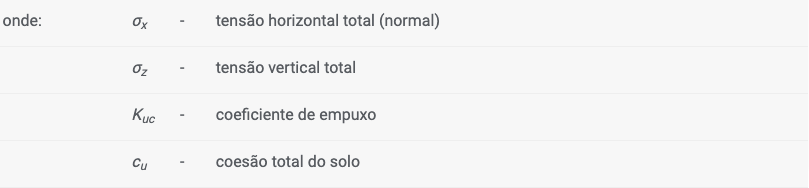
O coeficiente de empuxo Kuc é dado por:
![]()

Análise de Muros
A análise de verificação de muros pode ser executada através de:
![]() teoria dos estados limite (ao realizar a análise de acordo com EN 1997 ou LRFD, a estrutura é verificada de forma particular, de acordo com a Norma selecionada)
teoria dos estados limite (ao realizar a análise de acordo com EN 1997 ou LRFD, a estrutura é verificada de forma particular, de acordo com a Norma selecionada)![]() fator de segurança
fator de segurança
A capacidade de suporte do solo de fundação é analisada para ambos os casos.
As seguintes forças são consideradas na verificação:
![]() peso próprio do muro – depende da forma e peso volúmico do muro (definido através da caixa de diálogo “Material”) – é considerado o empuxo para muros com fundação abaixo do nível freático
peso próprio do muro – depende da forma e peso volúmico do muro (definido através da caixa de diálogo “Material”) – é considerado o empuxo para muros com fundação abaixo do nível freático
resistência da face frontal – ao introduzir a resistência da face frontal, a força correspondente atua como empuxo em repouso, empuxo passivo ou empuxo passivo reduzido![]() forças gravíticas em cunhas de terra – estas forças podem ser geradas dependendo da forma da parede
forças gravíticas em cunhas de terra – estas forças podem ser geradas dependendo da forma da parede
empuxo ativo ou empuxo em repouso atuante na estrutura – carregamento base da estrutura devido a empuxos de terra – dependendo da opção selecionada na janela “Configurações”, o empuxo é computado de forma a considerar, ou não, a redução dos valores característicos do solo introduzidos![]() forças devido à influência do nível freático ou pressão nos poros
forças devido à influência do nível freático ou pressão nos poros![]() forças devido a sobrecargas – cada força corresponde a uma sobrecarga introduzida. Se o valor da força devido à sobrecarga for nulo (a sobrecarga não tem qualquer efeito na estrutura), a sobrecarga não aparece na imagem, sendo apenas visível na tabela
forças devido a sobrecargas – cada força corresponde a uma sobrecarga introduzida. Se o valor da força devido à sobrecarga for nulo (a sobrecarga não tem qualquer efeito na estrutura), a sobrecarga não aparece na imagem, sendo apenas visível na tabela![]() forças aplicadas – as forças consideradas na análise são visíveis
forças aplicadas – as forças consideradas na análise são visíveis![]() forças devido à ação sísmica – a análise sísmica considera várias forças – aumento do empuxo de terra atuante na estrutura, redução do empuxo na face frontal da estrutura, ou força devido ao fluxo de água atrás da estrutura
forças devido à ação sísmica – a análise sísmica considera várias forças – aumento do empuxo de terra atuante na estrutura, redução do empuxo na face frontal da estrutura, ou força devido ao fluxo de água atrás da estrutura![]() malhas metálicas e reforços são visíveis e incluídas na análise
malhas metálicas e reforços são visíveis e incluídas na análise![]() ancoragem da base de muros
ancoragem da base de muros
Avaliação de Forças na Base da Fundação
Após computar as forças que atuam na estrutura, o programa determina a resultante das forças vertical Fv e horizontal Fh e calcula as forças que atuam na base da estrutura (força normal N e força de cisalhamento H):
![]()
![]()
Verificação – Estados Limite
O programa avalia as forças normal e de cisalhamento na base da fundação e realiza a verificação ao derrube e ao deslizamento. Para muros com fundações planas e dente definido, é possível considerar o dente da fundação como uma forma de pressão atuante na face frontal ou como se a base da fundação fosse inclinada.
Verificação ao derrube:
![]()

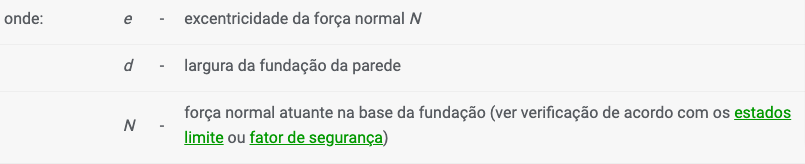
Verificação ao deslizamento:
![]()
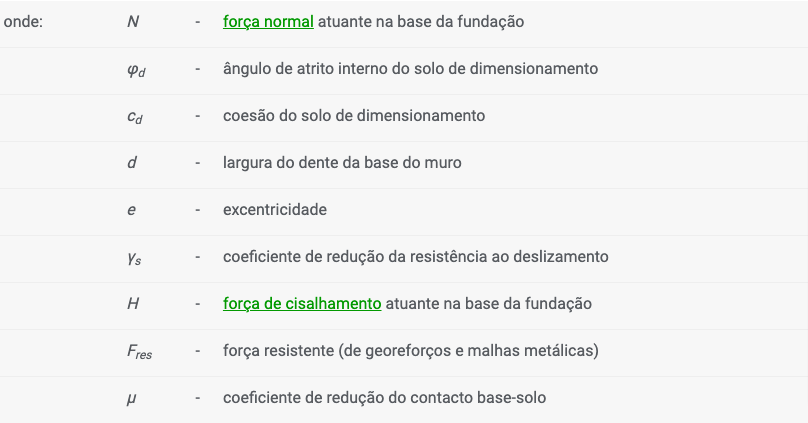
em que a excentricidade e:
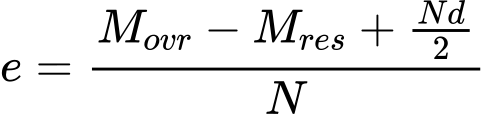
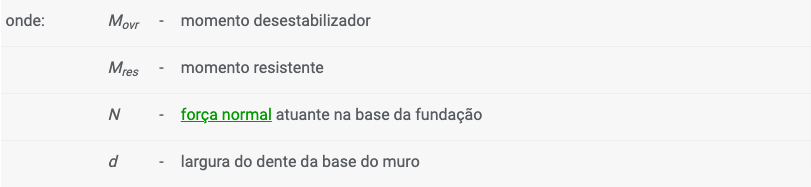
A componente horizontal das forças é considerada na força de cisalhamento e no momento desestabilizador. A componente vertical da força é considerada na força normal e no momento resistente. As forças e momentos resistentes também incluem as forças horizontais de georeforços e de malhas metálicas.
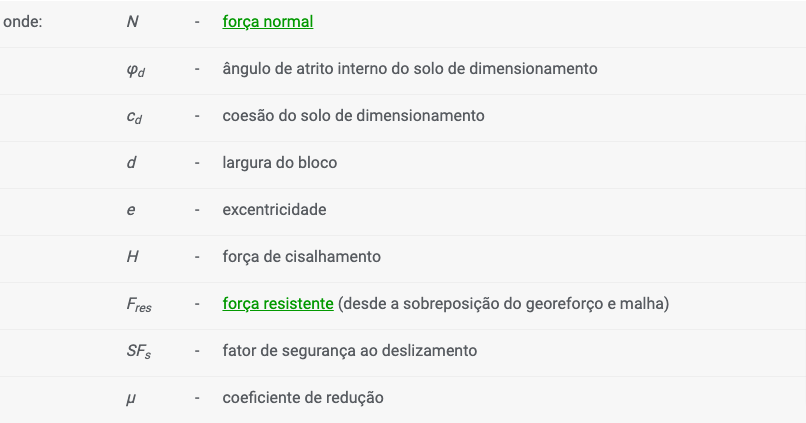
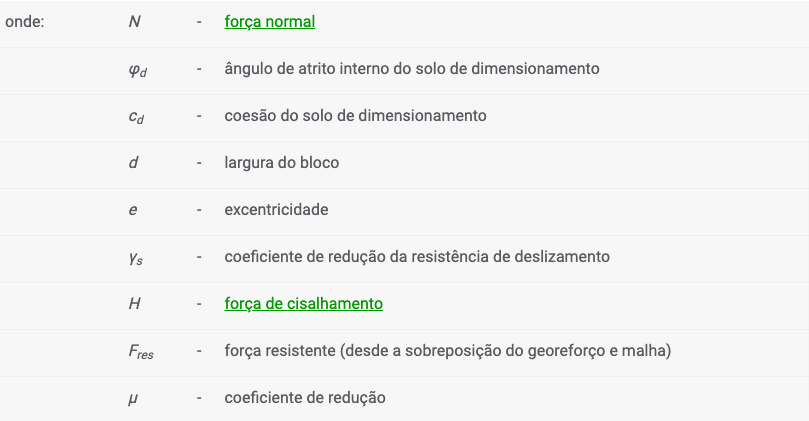
Verificação – Fator de Segurança
O programa avalia as forças normal e de cisalhamento na base da fundação e realiza a verificação ao derrube e ao deslizamento. Para muros com fundações planas e dente definido, é possível considerar o dente da fundação como uma forma de pressão atuante na face frontal ou como se a base da fundação fosse inclinada.
Verificação ao derrube:
![]()

Verificação ao deslizamento:
![]()
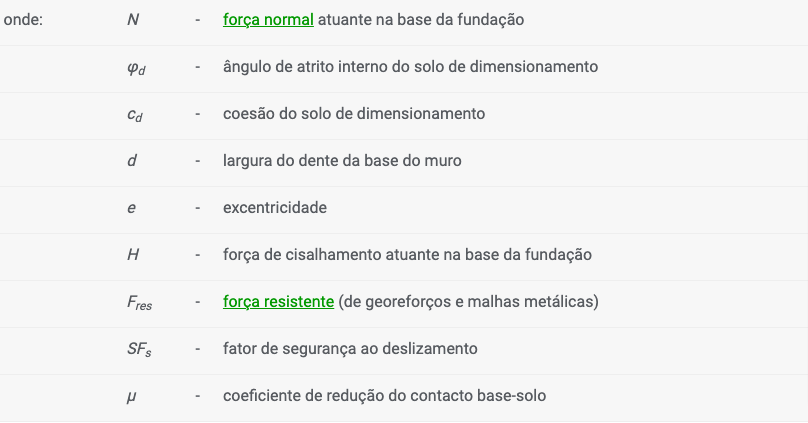
em que a excentricidade e:
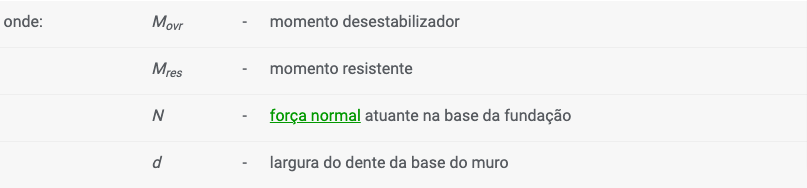
A componente horizontal das forças é considerada na força de cisalhamento e no momento desestabilizador. A componente vertical da força é considerada na força normal e no momento resistente. As forças e momentos resistentes também incluem as forças horizontais de georeforços e de malhas metálicas.
Deslizamento Interno
Este estado limite avalia a possibilidade da estrutura deslizar ao longo do reforço. Para o reforço definido, o programa obtém a superfície de deslizamento crítica, dentro do intervalo 45 – 90o medido a partir do limite do reforço.
Para cada superfície de deslizamento, o programa calcula as forças de cisalhamento e resistentes e realiza a verificação.
As forças de cisalhamento incluem:
![]() pressões ativas num muro fictício
pressões ativas num muro fictício
![]() forças devido a sobrecargas atrás da parede
forças devido a sobrecargas atrás da parede
As forças resistentes incluem:
![]() resistência da parede da estrutura contra o deslizamento (é calculada como no dimensionamento do muro)
resistência da parede da estrutura contra o deslizamento (é calculada como no dimensionamento do muro)
![]() atrito entre o reforço e o bloco deslizante
atrito entre o reforço e o bloco deslizante
![]() forças devido a outros reforços
forças devido a outros reforços
A força resistente devido ao atrito entre o reforço e o bloco deslizante é dada por:
![]()
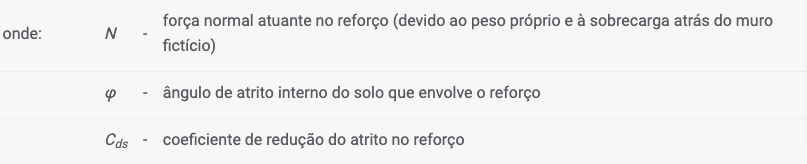
A verificação é realizada com base na secção “Análise de Muro”, de acordo com a teoria dos estados limite ou com o fator de segurança. A verificação deve garantir que:
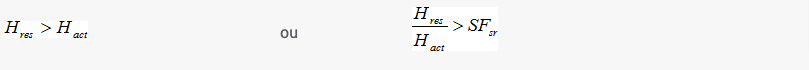

Reforços
Os reforços e malhas metálicas podem aumentar a estabilidade do muro. O parâmetro base dos reforços é a resistência à tração Rt. Todos os programas consideram um valor de dimensionamento para este parâmetro (à exceção do programa Redi-Rock wall), isto é, a resistência à tração do reforço é reduzida por coeficientes que consideram o efeito da durabilidade, deformações, condições químicas e danos na instalação. A força transmitida pelo reforço nunca pode exceder a tensão à tração atribuída Rt (é definido um valor padrão de 40 kN/m para gabiões).
Outra característica a definir é a resistência à remoção Tp. Este parâmetro determina o comprimento ancorado, isto é, o comprimento do reforço inserido no solo, para o qual o reforço está totalmente tensionado, atingindo o valor de Rt. Uma vez que os valores reais da resistência à remoção são difíceis de determinar, o programa permite três opções para o cálculo da força F transmitida pelo reforço.
Cálculo da força de remoção
A força de remoção F é dada por:
![]()
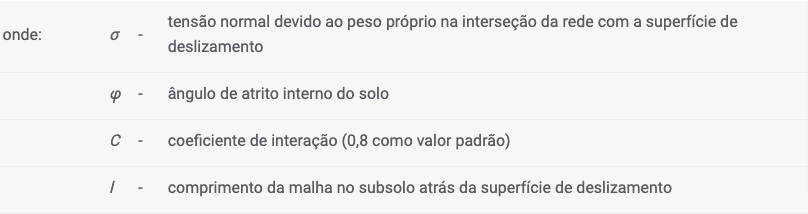
O cálculo do ângulo υa é descrito no capítulo Empuxo em Cunhas de Terra.
Introdução do comprimento ancorado do reforço lk
O comprimento ancorado lk deve ser definido. Este parâmetro é determinado pela força de cisalhamento desenvolvida entre a rede e o solo, que aumenta gradualmente desde zero até ao seu valor limite (medido a partir da extremidade do reforço fixa no solo).
![]()

Introdução da resistência à remoção da malha Tp
A força de remoção F é dada por:
![]()

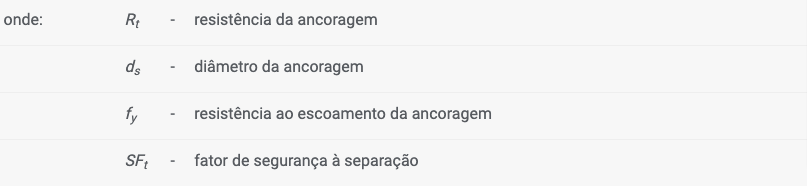
Ancoragem da Base
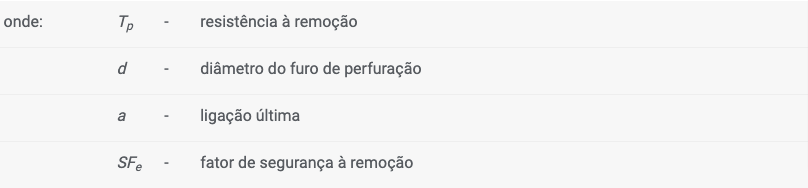
Pode ser definida uma ancoragem para a fundação da estrutura no programa “Muro de Flexão“. É necessário definir a localização da ancoragem, dimensões do furo de perfuração e espaçamento entre ancoragens.
São definidos dois estados limite de capacidade de suporte para as ancoragens:
![]() capacidade de suporte contra a remoção Re [kN/m]
capacidade de suporte contra a remoção Re [kN/m]
![]() resistência da ancoragem Rt [kN]
resistência da ancoragem Rt [kN]
A capacidade de suporte pode ser introduzida ou calculada a partir de valores introduzidos, através das seguintes expressões:
![]()
![]()
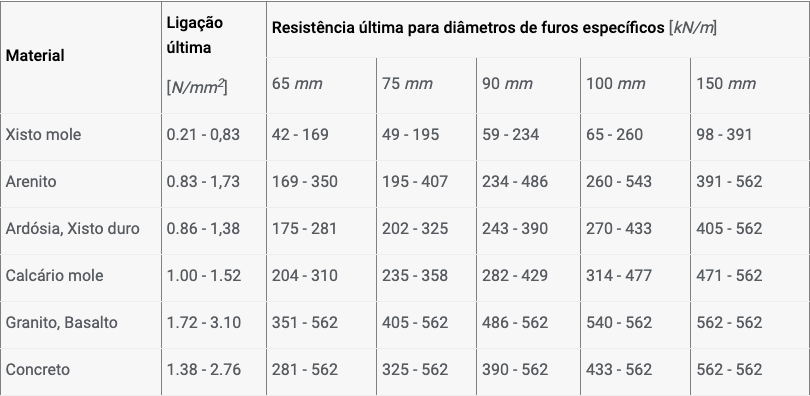
Valores aproximados para a capacidade de suporte contra a remoção
Consideração do Dente da Fundação
Existem duas opções para considerar o dente da base da estrutura, conforme mostram as figuras (nos programas “Muro de Flexão” e “Muro de Alvenaria“).
Se para a consideração do dente da fundação se assumir que a base da fundação é inclinada, então considera-se uma nova forma para a base da fundação e a resistência da face frontal da estrutura é considerada apenas até à profundidade da face frontal da estrutura.
Se para a consideração do dente da fundação se assumir a sua influência na resistência da face frontal, a análise assim que a base da fundação é plana (como se o dente não existisse), mas a face frontal da estrutura é considerada até à profundidade do dente. Neste caso, o valor da resistência da face frontal deve ser introduzido – caso contrário a influência do dente da fundação não é considerado.
O dente introduzido sob a fundação da parede é sempre considerado na resistência da face frontal da estrutura.
Capacidade de Suporte do Solo de Fundação
A análise de verificação da capacidade de suporte do solo de fundação considera as todas forças obtidas a partir de verificações para a estabilidade global da estrutura (teoria dos estados limite, fator de segurança). Para tal, são utilizadas as seguintes relações:
Normalmente, os diagramas de tensões na base das fundações são considerados constantes para fundações de comprimento reduzido.
![]()
![]()
Algumas Normas exigem a forma trapezoidal do diagrama de tensões. Neste caso, a verificação é realizada para o valor máximo σmax.
Para o cálculo da capacidade de carga do solo de fundação (no caso do muro estar assente sob fundações rasas) o programa permite calcular a carga de serviço ou de dimensionamento, que atua no centro da base da fundação. Ao transferir os dados e resultados para o programa “Sapata“, é possível calcular o recalque e a rotação da fundação corretamente. Ao assumir uma fundação em estacas na janela “Fundação”, é possível observar as forças internas na cabeça das estacas (para uma série de estacas), no centro da base da fundação (para uma malha plana de estacas).
Dimensionamento do Muro
Após calcular as forças que atuam na estrutura, o programa determina todas as forças internas para a secção em análise (força normal N, força de cisalhamento Q e momento M) e verifica a capacidade de suporte da secção, aplicando a configuração selecionada na secção “Análise de Muro”.
Apenas as forças que atuam acima da secção considerada (ver figura) são consideradas para o dimensionamento. Estas forças não são multiplicadas por nenhum coeficiente de dimensionamento.
O avanço frontal da estrutura, assim como o avanço posterior, são verificados para o carregamento devido ao momento fletor e à força de cisalhamento. A tensão na base da fundação pode ser assumida como constante (CSN) ou linear (EC).
Assumindo uma variação linear da tensão na base da fundação, a distribuição da tensão é dada por:
![]()
![]()
ou quando a tensão é excluída:
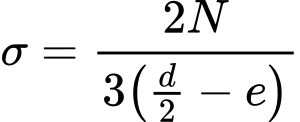
O momento fletor e a força de cisalhamento são determinados como reações desenvolvidas na viga em consola, como mostra a figura:
A verificação do avanço posterior da estrutura (armadura de tração superior no avanço da estrutura) é realizada apenas em alguns países, não sendo, normalmente, necessária. Os programas “Muro de Flexão” e “Muro Reforçado” permitem, na versão 5.5, o dimensionamento da armadura do avanço posterior da estrutura. Assume-se que a secção é carregada pelo peso próprio, cunha de terra, sobrecarga, força de ancoragem e força associada ao empuxo de terra. As forças devido ao empuxo apenas são consideradas caso tenham um impacte negativo na estabilidade da estrutura. As forças introduzidas pelo usuário não são consideradas.
A secção é verificada para o carregamento devido ao momento fletor e à força de cisalhamento.
Dimensionamento de Muros de Contrafortes
Após computar as forças atuantes na estrutura, o programa determina todas as forças internas na secção transversal verificada (foça de cisalhamento Q e momento M) e, de seguida, verifica a capacidade de suporte da secção transversal de acordo com a configuração selecionada na secção “Análise de muro”.
Haste do muro – direção horizontal
Momento máximo a meio vão entre contraventamentos, na parte frontal da haste do muro:
![]()
Momento máximo no contraventamento, na parte traseira da haste do muro:
![]()
Força de cisalhamento máxima:
![]()

Haste do muro – direção vertical
Momento máximo a meia altura do muro, na parte frontal da haste do muro:
![]()
Momento máximo na base, na parte traseira da haste do muro:
![]()
Força de cisalhamento máxima:
![]()

Avanço do muro – muro de contrafortes
Momento máximo a meia altura do muro, na parte frontal da haste do muro:
![]()
Momento máximo no contraventamento, na base do avanço do muro:
![]()
Força de cisalhamento máxima:
![]()

Dente do muro – muro de contrafortes
Momento máximo a meio vão entre contraventamentos, na parte superior do dente do muro:
![]()
Momento máximo no contraventamento, na base do dente do muro:
![]()
Força de cisalhamento máxima:
![]()

Muro de contrafortes
O contraforte é verificado como uma secção retangular. O cálculo das forças internas é semelhante ao cálculo realizado para a haste do muro em muros de flexão. As forças internas são multiplicadas pela largura do carregamento l+b (espaçamento entre contrafortes + espessura dos contrafortes).
Para as restantes verificações (Dente do muro – muro de contrafortes, Avanço do muro – muro de contrafortes), as forças internas são calculadas da mesma forma que no muro de flexão.
Estabilidade Interna de Gabiões
A estabilidade interna de muros gabião pode ser analisada através de:
![]() teoria dos estados limite
teoria dos estados limite
![]() fator de segurança
fator de segurança
A verificação de juntas entre blocos é realizada na janela “Dimensionamento“. A estrutura acima do bloco é carregada por empuxo ativo e as forças correspondentes são determinadas da mesma forma que para a verificação de todo o muro. É utilizado um enchimento solto na análise – em vez de enchimento rochoso colocado manualmente – mas o seu efeito pode ser simulado utilizando um ângulo de atrito interno muito elevado. É possível assumir que após algum tempo, devido à ação do agregado de enchimento, a tensão na malha reduz. A verificação para as tensões normais e de cisalhamento máximas é realizada para secções individuais do gabião. Através destas variáveis, é possível modificar a inclinação da face da estrutura com a criação de patamares ou aumentando a inclinação da face da parede α.
A carga aplicada ao bloco inferior é representada graficamente como:
A tensão normal no centro do bloco inferior é dada por:
![]()
![]()

A pressão atuante na face do bloco inferior é determinada como uma pressão ativa aumentada:
![]()
![]()
![]()
![]()
![]()

As larguras das malhas do bloco inferior, por cada metro de desenvolvimento do gabião, são:
![]()
![]()

O programa permite a análise de gabiões com malhas simples ou duplas, colocadas entre blocos. Para as malhas duplas, o valor introduzido para a resistência à tração (janela “Material” – caixa de diálogo “Editar material“) deve ser o dobro do valor assumido para malhas simples.
Estabilidade Interna de Gabiões – Fator de Segurança
Os seguintes casos são assumidos ao verificar a estabilidade interna de um muro de gabiões, através do conceito do fator de segurança:
1) Verificação da estabilidade ao derrube:
![]()

2) Verificação ao deslizamento:
![]()
3) Verificação da capacidade de suporte considerando pressões laterais:
![]()
![]()

4) Verificação da capacidade de suporte das juntas entre blocos:
![]()
![]()
![]()

Estabilidade Interna de Gabiões – Estados Limite
Os parâmetros reduzidos do material dos gabiões, que dependem dos coeficientes definidos na secção “Análise de muro”, são utilizados nas análises de verificação.
1) Verificação ao derrube:
![]()

2) Verificação do deslizamento:
![]()
3) Verificação da capacidade de suporte considerando pressões laterais:
![]()
![]()

4) Verificação da capacidade de suporte das juntas entre blocos:
![]()
![]()
![]()

Cálculo de Forças em Encontros de Pontes
A análise de encontros é realizada por 1 m (1ft). Todas as forças consideradas na análise são ajustadas pelo programa da seguinte forma:
![]() o peso próprio do encontro, assumido para 1 m (1ft), é calculado a partir da secção transversal introduzida
o peso próprio do encontro, assumido para 1 m (1ft), é calculado a partir da secção transversal introduzida
![]() as reações geradas pela ponte e pela laje de aproximação são introduzidas em kN (kpi), considerando os valores para todo o encontro, que são divididos pelo comprimento do encontro durante a análise.
as reações geradas pela ponte e pela laje de aproximação são introduzidas em kN (kpi), considerando os valores para todo o encontro, que são divididos pelo comprimento do encontro durante a análise.
![]() o empuxo do solo é determinado para 1 m (1ft) e multiplicado pelo rácio comprimento da carga devido ao solo / comprimento do encontro
o empuxo do solo é determinado para 1 m (1ft) e multiplicado pelo rácio comprimento da carga devido ao solo / comprimento do encontro
![]() o peso das cunhas de solo é determinado para 1 m (1ft) e multiplicado pelo rácio comprimento da carga devido ao solo / comprimento do encontro
o peso das cunhas de solo é determinado para 1 m (1ft) e multiplicado pelo rácio comprimento da carga devido ao solo / comprimento do encontro
![]() a sobrecarga é determinada para 1 m (1ft) e multiplicada pelo rácio comprimento da carga devido ao solo / comprimento do encontro
a sobrecarga é determinada para 1 m (1ft) e multiplicada pelo rácio comprimento da carga devido ao solo / comprimento do encontro
![]() as forças introduzidas e a resistência da face frontal são assumidas para 1 m sem redução
as forças introduzidas e a resistência da face frontal são assumidas para 1 m sem redução
![]() paredes ala – o peso próprio das paredes ala é computado a partir da sua geometria; este é dividido pelo comprimento do encontro antes de ser adicionado ao dimensionamento da haste e à verificação da fundação (é da responsabilidade do usuário incluir, ou excluir, na análise o efeito das paredes ala).
paredes ala – o peso próprio das paredes ala é computado a partir da sua geometria; este é dividido pelo comprimento do encontro antes de ser adicionado ao dimensionamento da haste e à verificação da fundação (é da responsabilidade do usuário incluir, ou excluir, na análise o efeito das paredes ala).
A computação de forças individuais dos encontros é descrita com mais detalhe no capítulo “Análise de Muros”.
Todas as forças atuantes na junta da fundação que são consideradas na análise de verificação (exceto para a resistência da face frontal) são multiplicadas pelo rácio comprimento do encontro / comprimento da fundação.
Empuxo de Terra Passivo Reduzido
A evolução do empuxo de terra passivo σp corresponde ao deslocamento máximo da estrutura em direção ao solo. No entanto, este deslocamento pode não ocorrer (ex.: no caso de cortinas de contenção fixas) e a estrutura fica carregada pelo empuxo de terra passivo reduzido σps. O valor do empuxo de terra passivo reduzido σps pode variar entre os valores do empuxo de terra em repouso σr (no caso de não existir deformação) até ao valor do empuxo de terra passivo σp. A figura mostra a relação dos valores para o empuxo de terra, de um solo não coesivo (resistência do solo), com os valores do rácio do deslocamento real d pelo deslocamento máximo dmax (ao introduzir o empuxo de terra passivo σp).
Solo Grampeado
O programa “Solo Grampeado” permite as seguintes verificações:
![]() Verificação da estabilidade interna da estrutura (superfícies de deslizamento planas ou quebradas, capacidade de suporte dos grampos)
Verificação da estabilidade interna da estrutura (superfícies de deslizamento planas ou quebradas, capacidade de suporte dos grampos)
![]() Verificação do muro fictício – verificação igual à do muros de gravidade
Verificação do muro fictício – verificação igual à do muros de gravidade
![]() Verificação do cobrimento em concreto da estrutura (dimensionamento)
Verificação do cobrimento em concreto da estrutura (dimensionamento)
![]() Verificação da malha (dimensionamento)
Verificação da malha (dimensionamento)
![]() Verificação da estabilidade global através do programa “Estabilidade de Taludes“
Verificação da estabilidade global através do programa “Estabilidade de Taludes“
Análise da Estabilidade Interna
A estabilidade interna de uma estrutura pode ser verificada para dois tipos de superfícies de deslizamento:
![]() Superfície de deslizamento plana
Superfície de deslizamento plana
![]() Superfície de deslizamento quebrada
Superfície de deslizamento quebrada
Em ambos os casos, a superfície de deslizamento é verificada para o ângulo de variação ϑ.
Ao executar a otimização da análise, o programa realiza o cálculo, para cada trecho, considerando uma variação do ângulo da superfície de deslizamento ν desde 1 até 89 graus, um grau de cada vez.
A análise de verificação da estabilidade interna pode ser realizada através do fator de segurança ou da teoria dos estados limite, conforme o definido na secção “Análise de muro”.
A análise verifica se um rácio entre forças resistentes e forças de cisalhamento, atuantes na superfície de deslizamento, é superior ao fator de segurança introduzido. As seguintes forças são consideradas:
Forças de cisalhamento:
![]() componente da força de gravidade paralela à superfície de deslizamento
componente da força de gravidade paralela à superfície de deslizamento
![]() no caso de superfícies de deslizamento quebradas – a componente do empuxo de terra ativo atuante na parte vertical da estrutura e paralela à superfície de deslizamento (o empuxo é determinado sem redução dos parâmetros introduzidos)
no caso de superfícies de deslizamento quebradas – a componente do empuxo de terra ativo atuante na parte vertical da estrutura e paralela à superfície de deslizamento (o empuxo é determinado sem redução dos parâmetros introduzidos)
![]() forças horizontais devido a sismos
forças horizontais devido a sismos
Forças resistentes:
![]() atrito e coesão do solo ao longo da superfície de deslizamento
atrito e coesão do solo ao longo da superfície de deslizamento
![]() somatório das forças transmitidas pelos grampos
somatório das forças transmitidas pelos grampos
Análise da Capacidade de Suporte dos Grampos
As seguintes capacidades de suporte podem ser introduzidas ou calculadas, para cada grampo:

As características de resistência dos grampos representam os parâmetros base para computar a capacidade de suporte total dos grampos.
A resistência do grampo à rotura é calculada através da expressão:
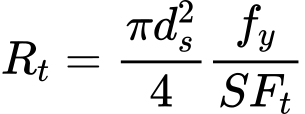
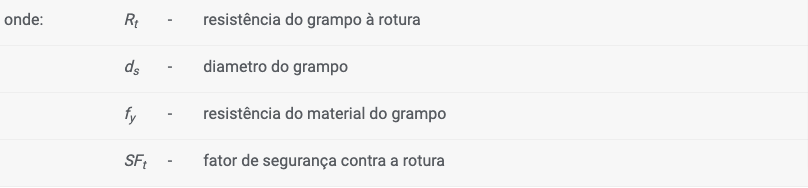
A capacidade de suporte do grampo contra a remoção é calculada através de uma das seguintes opções:
1. cálculo a partir do atrito superficial:
![]()
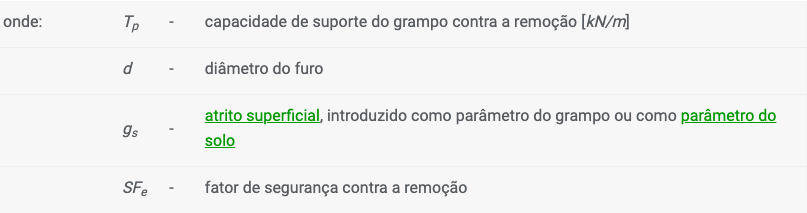
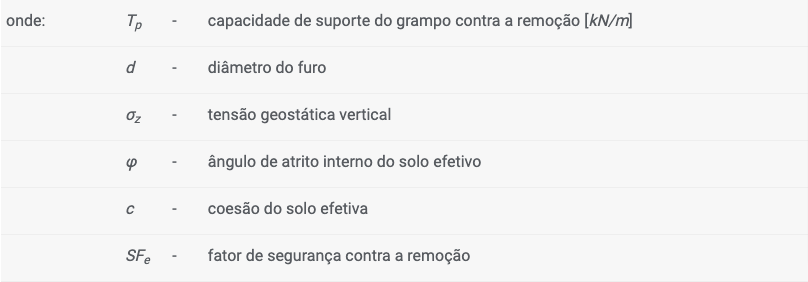
2. cálculo a partir da tensão efetiva:
![]()
onde:
![]()
3. cálculo de acordo com HA 68/94
![]()
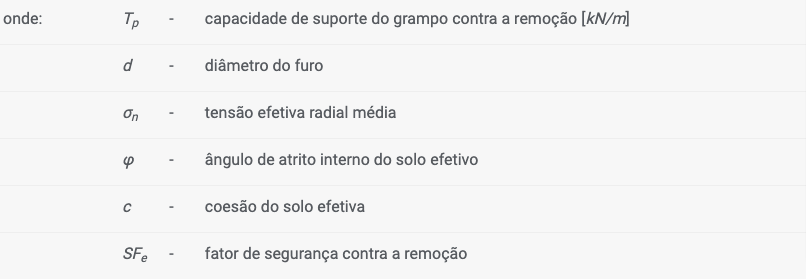
A tensão efetiva radial média σn é calculada através da seguinte fórmula:
![]()
![]()
onde:
![]()
A resistência da cabeça do grampo é avaliada através da seguinte fórmula:
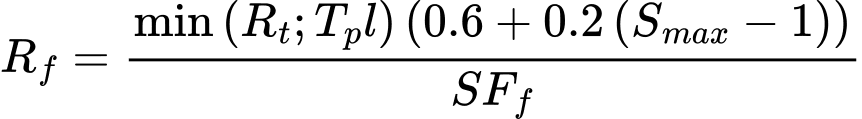
Se o grampo não estiver ancorado ao cobrimento da estrutura, é possível definir a resistência da cabeça do grampo como zero.
Bibliografia:
FHWA0-IF-03-017
Valores Recomendados para o Atrito Superficial
A tabela é baseada em ensaios de campo e de laboratório.
Atrito superficial: Classificação de grampos perfurados

Notas:
1) A determinação do atrito superficial deve fazer parte de um ensaio geotécnico
2) Resistência de cone, ensaio CPT (de acordo com DIN EN ISO 22476-1)
3) Coesão total do solo
4) Resistência à compressão uniaxial
Bibliografia:
EA-Pfähle, ISBN: 978-3-433-03005-9
Os valores da tabela são baseados na classificação de solos e rochas.
Força de ligação estimada para grampos inseridos em solos e rochas (fonte: Elias a Juran, 1991)

Nota: Converter valores em kPa para psf ao multiplicar por 20.9. Converter valores em kPa para psi ao multiplicar por 0,145.
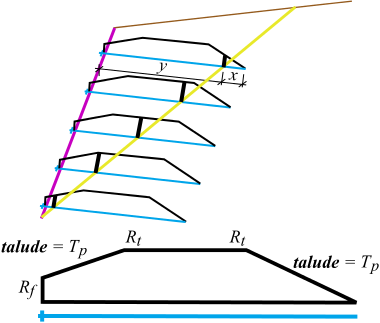
Capacidade de Suporte Total dos Grampos
A capacidade de suporte dos grampos é determinada com base na localização da sua intersecção com a superfície de deslizamento. Se um grampo não intersetar a superfície de deslizamento, então este não é considerado no cálculo. Se o grampo atravessar a superfície de deslizamento, então a sua capacidade de suporte é determinada através de:
![]()
Verificação – Fator de Segurança
A análise verifica se o rácio entre as forças resistente e de cisalhamento atuantes na superfície de deslizamento é superior ao fator de segurança introduzido.
O fator de segurança para as forças de deslizamento introduzidas é dado por:
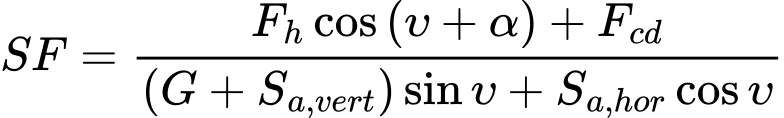
![]()
![]()

Verificação – Teoria dos Estados Limite
A análise verifica se as forças passivas Fp atuantes na superfície de deslizamento são superiores às forças ativas e Fa:
![]()
![]()
![]()
![]()
![]()

Força dos Grampos
O valor do empuxo de terra ativo é reduzido pelo coeficiente kn. O valor recomendado (determinado experimentalmente) é kn = 0.85.
As forças transmitidas por cada grampo são determinadas de forma a que parte do empuxo de terra calculado seja atribuído a cada trecho. Cada grampo é carregado pela parte correspondente do empuxo de terra ativo.
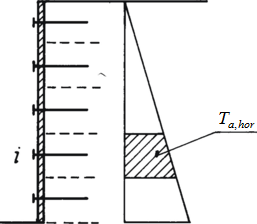
A força do grampo é dada por:
![]()
Dimensionamento do Cobrimento em Croncreto
O cobrimento em concreto de um talude grampeado é dimensionado para suster o empuxo de terra ativo. Assim, assume-se que a estrutura é subdividida em faixas de dimensionamento intermédias.
Na direção vertical, a cabeça do grampo é modelada como um apoio e articulação de juntas entre trechos.
Na direção horizontal, o programa gera (por defeito) uma estrutura com cinco apoios uniformemente carregados pelo valor do empuxo ativo, até à profundidade da cabeça do grampo.
O programa também permite a verificação do cobrimento em concreto da estrutura carregado pelo momento fletor.
A figura mostra o esquema construtivo do modelo de dimensionamento e as cargas respetivas:
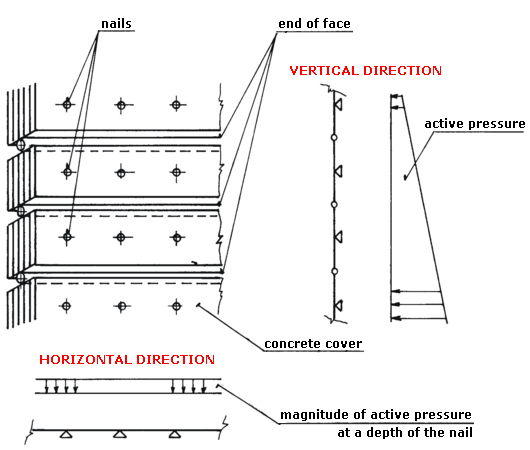
Verificação da Malha
O dimensionamento da malha implica que a camada exposta seja composta por solo ou por rocha fortemente afetada pela exposição.
São realizadas as seguintes análises:
1) Verificação para a resistência ao cisalhamento da pregagem
![]()

2) Verificação para a resistência ao punçoamento da malha
![]()

3) Verificação para a resistência ao cisalhamento da malha
![]()

4) Verificação para a deformação combinada na pregagem
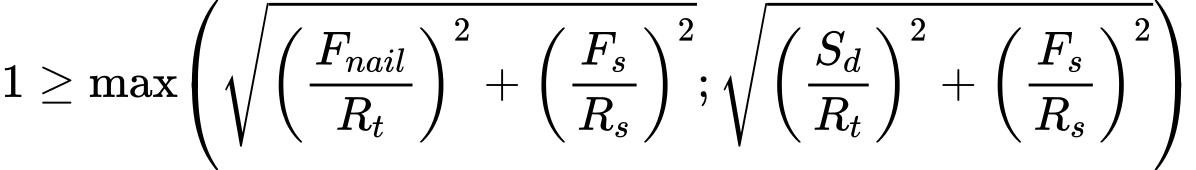
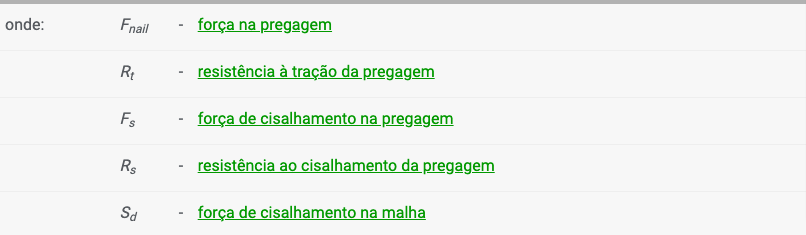
Bibliografia:
Krist O., Raithel M., Weingart K.: “Bemessung von Drathgeflechten zur Stabilisierung von Böschungen”. EI-Eisenbahningenieur, March 2015, 14-19.
Força de Cisalhamento na Pregagem
Na verificação da capacidade de carga da pregagem, é considerada a superfície de deslizamento para a profundidade máxima da camada exposta. A força de cisalhamento Fs é determinada a partir da forças atuantes no bloco de solo.
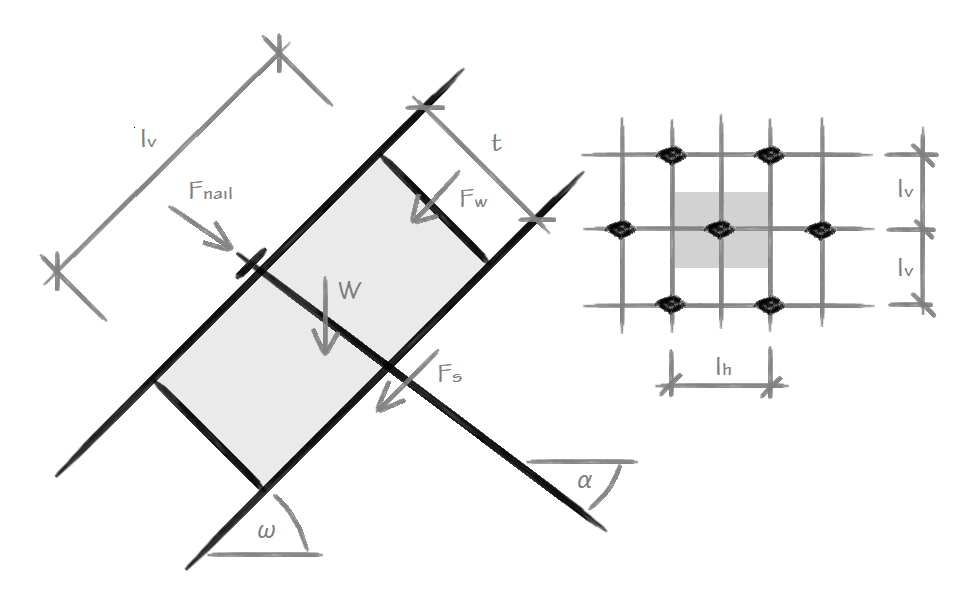
![]()
Caso o fluxo de água seja considerado, o programa realiza o cálculo considerando a existência de água em toda a camada exposta.
Força de Cisalhamento na Malha
O programa calcula automaticamente duas formas de superfícies de deslizamento (no bloco de solo formado pela área entre pregagens) e encontra a força de cisalhamento máxima.
Superfície de deslizamento plana – o programa encontra a força de cisalhamento máxima ao longo de toda a espessura da camada exposta.
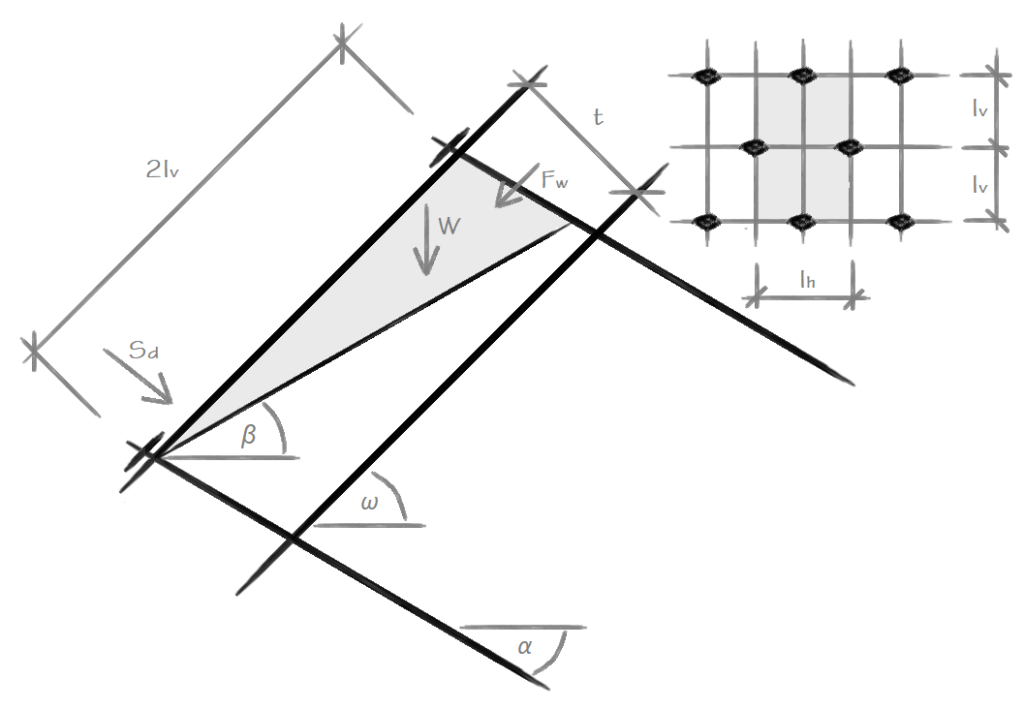
![]()
Superfície de deslizamento fraturada – o programa encontra a força de cisalhamento máxima ao longo de toda a espessura, com diferentes inclinações na base do bloco, da camada exposta.
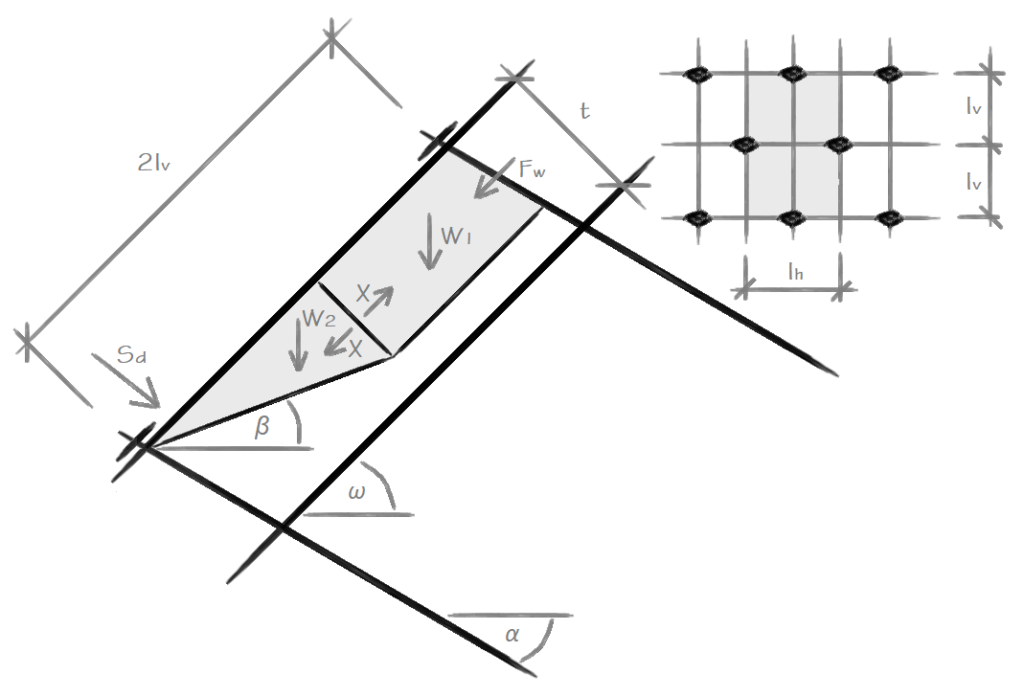
Ao analisar superfícies de deslizamento fraturadas, a força entre os blocos X é calculada da seguinte forma:
![]()
![]()

Caso o fluxo de água seja considerado, o programa realiza o cálculo considerando a existência de água em toda a camada exposta. O ângulo de pressão de cona influencia a transmissão da força da pregagem através da camada exposta.
Influência da Pressão de Cone
A inclinação da pressão de cone determina a transmissão da força da pregagem através da camada exposta. Esta é considerada no cálculo da força de cisalhamento atuante na malha, que reduz o espaçamento horizontal entre pregagens e a largura do bloco de solo. O resultado da redução apresenta uma forma trapezoidal do bloco de solo modificada para um retângulo de largura lh,red.
O ângulo de pressão de cone θ está compreendido entre o intervalo de 30° a 80°. O raio da pressão de cone na parte superior rcone é considerado como metade do comprimento da cabeça da pregagem lw.
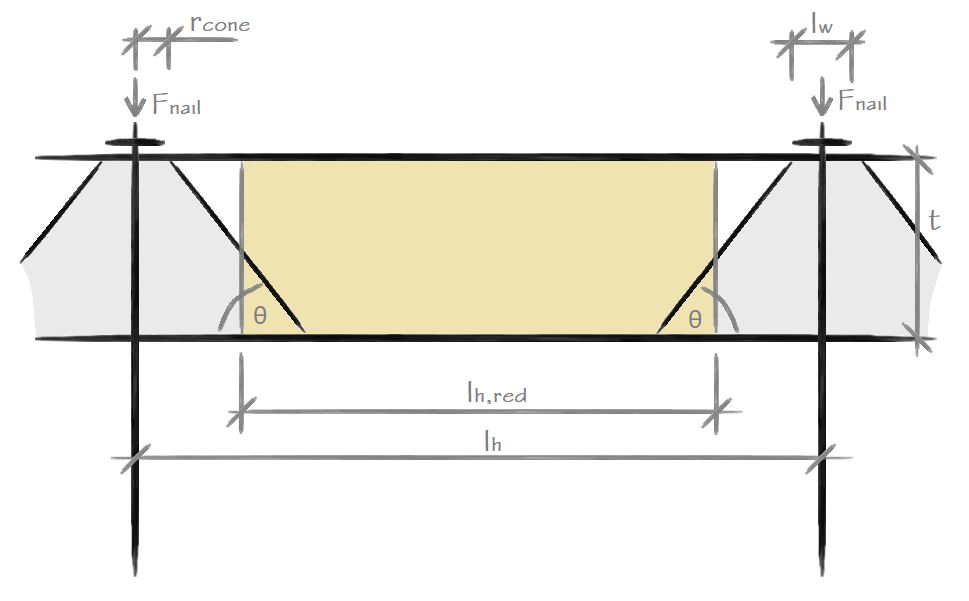
![]()
Influência do Fluxo de Água
A força Fw considera o efeito do fluxo de água. Esta entre no cálculo da força de cisalhamento na pregagem e da força de cisalhamento na malha.
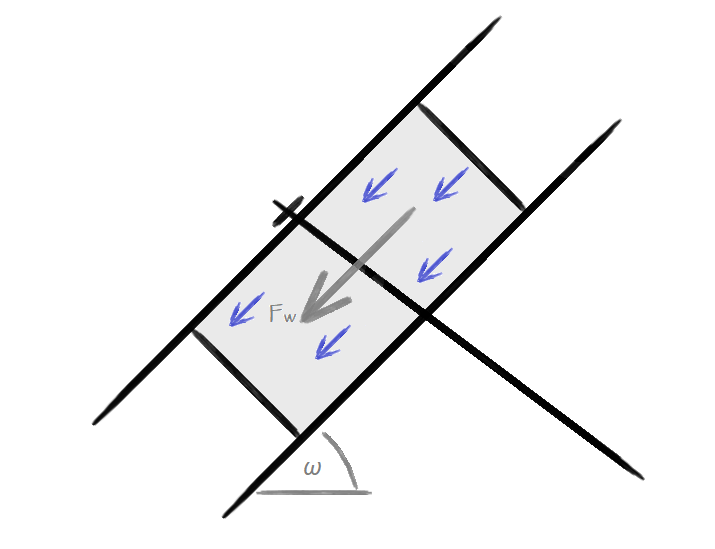
![]()
Dimensionamento de Escavações
O software GEO5 permite o dimensionamento completo e a análise de vários tipos de estruturas de contenção verticais. Os muros de contenção podem ser ancorados, não ancorados ou reforçados.
O programa para a análise de muros de contenção ancorados ou reforçados é o “Verificação de Contenções”. O programa permite calcular o comportamento real da estrutura em diferentes etapas da construção, calcular as deformações e as pressões atuantes na estrutura, verificar a estabilidade interna das ancoragens e verificar as secções transversais da estrutura, que pode ser testada para diferentes materiais (metal, plástico, madeira ou concreto armado).
O programa “Projeto de Contenções” pode ser utilizado para o dimensionamento rápido de estruturas ancoradas ou não ancoradas. O programa calcula o comprimento necessário da estrutura e as suas forças internas. A verificação da secção transversal também pode ser realizada (concreto, metal, madeira ou plástico).
Pode ser aplicada um tipo de estrutura de contenção particular para impedir o deslizamento de terras, conhecido como estacas anti-deslizante. O programa “Estaca anti-deslizante” permite a análise deste tipo de estruturas.
Introdução da Secção Transversal
A lista da caixa de diálogo “Editar secção” contém vários tipos de estruturas de contenção:
![]() Cortina de estacas
Cortina de estacas
![]() Parede de secção retangular em concreto armado
Parede de secção retangular em concreto armado
![]() Estacas-prancha
Estacas-prancha
![]() Perfil Metálico tipo I
Perfil Metálico tipo I
![]() Estacas-prancha de plástico (vinil)
Estacas-prancha de plástico (vinil)
![]() Perfil Metálico tipo 2xU
Perfil Metálico tipo 2xU
![]() Cortina de escadas com perfis metálicos
Cortina de escadas com perfis metálicos
![]() Tubo metálico
Tubo metálico
![]() Secções definidas pelo usuário
Secções definidas pelo usuário
As secções transversais podem ser guardadas no “Catálogo do usuário” (botão “Catálogo do usuário“).

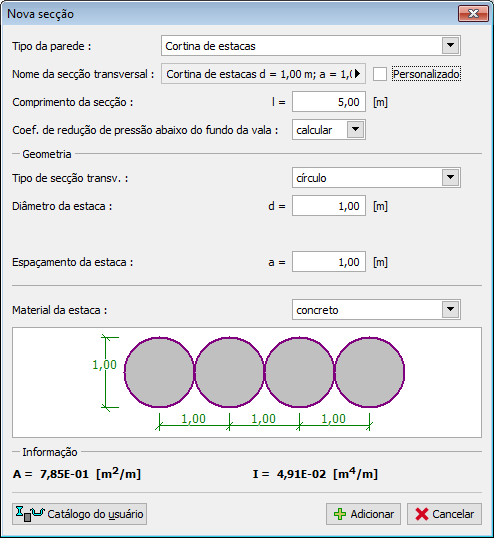
Cortina de Estacas
A cortina de estacas implica a introdução dos seguintes dados:
![]() Nome da secção transversal (o programa gera um nome automaticamente que pode ser alterado clicando em “Personalizado“)
Nome da secção transversal (o programa gera um nome automaticamente que pode ser alterado clicando em “Personalizado“)
![]() Coeficiente de redução de pressão abaixo do fundo da vala – este coeficiente é utilizado para reduzir as pressões abaixo do fundo da vala para o cálculo de contenções suportadas – pode ser introduzido ou calculado automaticamente (para contenções clássicas não suportadas este coeficiente é igual a 1.0)
Coeficiente de redução de pressão abaixo do fundo da vala – este coeficiente é utilizado para reduzir as pressões abaixo do fundo da vala para o cálculo de contenções suportadas – pode ser introduzido ou calculado automaticamente (para contenções clássicas não suportadas este coeficiente é igual a 1.0)
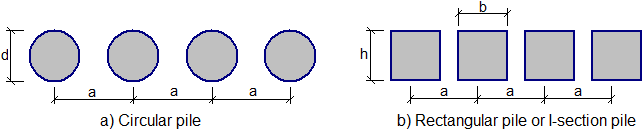
![]() Tipo da secção transversal (circular, retangular)
Tipo da secção transversal (circular, retangular)
![]() Diâmetro da estaca d e espaçamento entre estacas a
Diâmetro da estaca d e espaçamento entre estacas a
![]() Material da estaca (concreto, madeira)
Material da estaca (concreto, madeira)
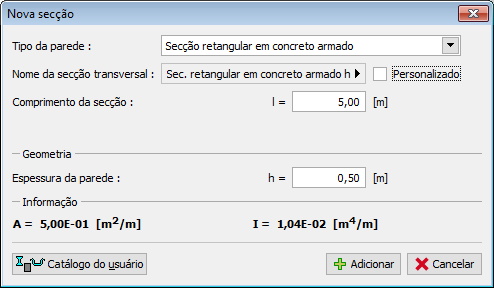
Parede de Secção Retangular em Concreto Armado
A parede de secção retangular em concreto armado implica a introdução dos seguintes dados:
![]() Nome da secção transversal (o programa gera um nome automaticamente que pode ser alterado clicando em “Personalizado“)
Nome da secção transversal (o programa gera um nome automaticamente que pode ser alterado clicando em “Personalizado“)
![]() Espessura da parede h
Espessura da parede h
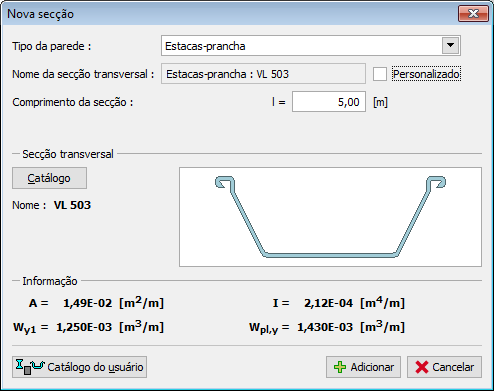
Estacas-prancha
As estacas-prancha implicam a introdução dos seguintes dados:
![]() Nome da secção transversal (o programa gera um nome automaticamente que pode ser alterado clicando em “Personalizado“)
Nome da secção transversal (o programa gera um nome automaticamente que pode ser alterado clicando em “Personalizado“)
![]() Tipo da secção transversal – selecionado na caixa de diálogo “Catálogo de Perfis” (botão “Catálogo“)
Tipo da secção transversal – selecionado na caixa de diálogo “Catálogo de Perfis” (botão “Catálogo“)
O catálogo de perfis contém várias classes de estacas-prancha e revestimentos, de diferentes fornecedores (ver em baixo). Se utilizar outro tipo de produtos, por favor contacte-nos (hotline@fine.cz) para podermos implementa-los no nosso catálogo.
Bibliografia:
Tipos de estacas-prancha implementados no nosso catálogo:
Estacas-prancha metálicas:
![]() Vítkovice steel – Product catalog of sheet piles
Vítkovice steel – Product catalog of sheet piles
![]() Arcelor Mittal – Steel Sheet Piling, General Catalogue 2012
Arcelor Mittal – Steel Sheet Piling, General Catalogue 2012
![]() ThyssenKrupp Bautechnik – Sheet Piling Handbook
ThyssenKrupp Bautechnik – Sheet Piling Handbook
![]() Chinese standard GB/T 20933-2014 Hot rolled sheet pile
Chinese standard GB/T 20933-2014 Hot rolled sheet pile
![]() Bethlehem Steel Sheet Piling
Bethlehem Steel Sheet Piling
![]() Gerdau Steel Sheet Piling
Gerdau Steel Sheet Piling
Estacas-prancha metálicas moldadas a frio:
![]() Mer Lion Metals – Cold Formed Steel Sheet Piles Catalogue
Mer Lion Metals – Cold Formed Steel Sheet Piles Catalogue
Revestimentos de valas:
![]() ThyssenKrupp Bautechnik – Kaltgewalzte Spundwandprofile – Kanaldielen
ThyssenKrupp Bautechnik – Kaltgewalzte Spundwandprofile – Kanaldielen
Estacas-prancha O WOM/WOF:
![]() Mer Lion Metals – Steel Sheet Piles Catalogue
Mer Lion Metals – Steel Sheet Piles Catalogue
![]() PilePro Group Company – Sheet Pile Connectors
PilePro Group Company – Sheet Pile Connectors
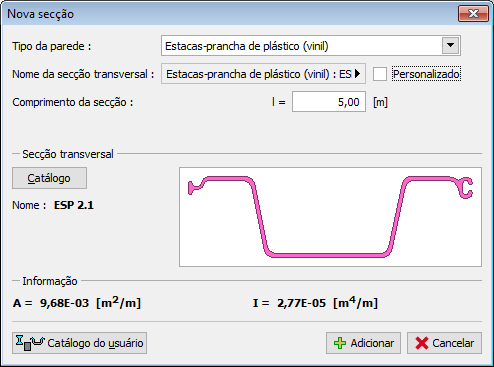
Estacas-prancha de Plástico (Vinil)
As estacas-prancha de plástico implicam a introdução dos seguintes dados:
![]() Nome da secção transversal (o programa gera um nome automaticamente que pode ser alterado clicando em “Personalizado“)
Nome da secção transversal (o programa gera um nome automaticamente que pode ser alterado clicando em “Personalizado“)
![]() Comprimento da secção l
Comprimento da secção l
![]() Tipo da secção transversal – selecionado na caixa de diálogo “Catálogo de Perfis” (botão “Catálogo“)
Tipo da secção transversal – selecionado na caixa de diálogo “Catálogo de Perfis” (botão “Catálogo“)
O catálogo de perfis contém várias classes de estacas-prancha e revestimentos, de diferentes fornecedores (ver em baixo). Se utilizar outro tipo de produtos, por favor contacte-nos (hotline@fine.cz) para podermos implementa-los no nosso catálogo.
As estacas-prancha de plástico não apresentam muita resistência à flexão e sofrem deformações bastante superiores às paredes de contenção metálicas ou em concreto. O método corrente para determinar o módulo de deformação (Schmitt) não pode ser utilizado em materiais plásticos. Se o método de Schmitt for selecionado, o programa altera automaticamente para o método “Vinil“. Neste caso, o módulo de deformação é calculado a partir do módulo edométrico do solo – kh = 2/3 Eoed.
Os outros métodos mantêm-se, como para os outros tipos de secções.
A verificação da capacidade de suporte de estacas-prancha de plástico pode ser executada na janela “Dimensionamento“.
Bibliografia:
![]() Katalog Everlast Synthetic Products, LLC – pode ser encontrado em https://everlastseawalls.com/seawall-products/vinyl-sheet-piling
Katalog Everlast Synthetic Products, LLC – pode ser encontrado em https://everlastseawalls.com/seawall-products/vinyl-sheet-piling
Perfil Metálico Tipo I
Os perfis metálicos tipo I implicam a introdução dos seguintes dados:
![]() Nome do perfil transversal (o programa gera um nome automaticamente que pode ser alterado clicando em “Personalizado“)
Nome do perfil transversal (o programa gera um nome automaticamente que pode ser alterado clicando em “Personalizado“)
![]() Coeficiente de redução da pressão abaixo do fundo da vala – este coeficiente é utilizado para reduzir as pressões abaixo do fundo da vala, para calcular contenções suportadas – pode ser introduzido ou calculado automaticamente (para contenções clássicas não suportadas este coeficiente é igual a 1.0)
Coeficiente de redução da pressão abaixo do fundo da vala – este coeficiente é utilizado para reduzir as pressões abaixo do fundo da vala, para calcular contenções suportadas – pode ser introduzido ou calculado automaticamente (para contenções clássicas não suportadas este coeficiente é igual a 1.0)
![]() Comprimento do perfil l
Comprimento do perfil l
![]() Espaçamento entre perfis
Espaçamento entre perfis
![]() Tipo do perfil transversal – selecionado na caixa de diálogo “Catálogo de Perfis” (botão “Catálogo“), ou na caixa de diálogo “Editor do perfil” (botão “Soldada“)
Tipo do perfil transversal – selecionado na caixa de diálogo “Catálogo de Perfis” (botão “Catálogo“), ou na caixa de diálogo “Editor do perfil” (botão “Soldada“)

Perfil Metálico Tipo 2xU
Os perfis metálicos tipo 2xU implicam a introdução dos seguintes dados:
![]() Nome do perfil transversal (o programa gera um nome automaticamente que pode ser alterado clicando em “Personalizado“)
Nome do perfil transversal (o programa gera um nome automaticamente que pode ser alterado clicando em “Personalizado“)
![]() Coeficiente de redução da pressão abaixo do fundo da vala – este coeficiente é utilizado para reduzir as pressões abaixo do fundo da vala, para calcular contenções suportadas – pode ser introduzido ou calculado automaticamente (para contenções clássicas não suportadas este coeficiente é igual a 1.0)
Coeficiente de redução da pressão abaixo do fundo da vala – este coeficiente é utilizado para reduzir as pressões abaixo do fundo da vala, para calcular contenções suportadas – pode ser introduzido ou calculado automaticamente (para contenções clássicas não suportadas este coeficiente é igual a 1.0)
![]() Comprimento do perfil l
Comprimento do perfil l
![]() Espaçamento entre perfis
Espaçamento entre perfis
![]() Tipo do perfil transversal – selecionado na caixa de diálogo “Catálogo de Perfis” (botão “Catálogo“), ou na caixa de diálogo “Editor do perfil” (botão “Soldada“)
Tipo do perfil transversal – selecionado na caixa de diálogo “Catálogo de Perfis” (botão “Catálogo“), ou na caixa de diálogo “Editor do perfil” (botão “Soldada“)

Cortina de Estacas com Perfis Metálicos
A cortina de estacas com perfis metálicos implica a definição de:
![]() Nome do perfil metálico (o programa gera um nome por defeito que pode ser alterado através da opção “Personalizado“)
Nome do perfil metálico (o programa gera um nome por defeito que pode ser alterado através da opção “Personalizado“)
![]() Coeficiente de redução da preção abaixo do fundo da vala – este coeficiente é utilizado para reduzir pressões abaixo do fundo da vala para o cálculo de contenções reforçadas – pode ser inserido ou calculado automaticamente (para contenções clássicas não reforçadas este coeficiente é igual a 1.0)
Coeficiente de redução da preção abaixo do fundo da vala – este coeficiente é utilizado para reduzir pressões abaixo do fundo da vala para o cálculo de contenções reforçadas – pode ser inserido ou calculado automaticamente (para contenções clássicas não reforçadas este coeficiente é igual a 1.0)
![]() Tipo de secção transversal (circular, quadrada)
Tipo de secção transversal (circular, quadrada)
![]() Diâmetro da estaca d e espaçamento a
Diâmetro da estaca d e espaçamento a
![]() Perfil metálico (tipo I, tubular, tipo 2xU ou soldado) – é selecionado na caixa de diálogo “Catálogo de perfis” (botão “Catálogo“)
Perfil metálico (tipo I, tubular, tipo 2xU ou soldado) – é selecionado na caixa de diálogo “Catálogo de perfis” (botão “Catálogo“)
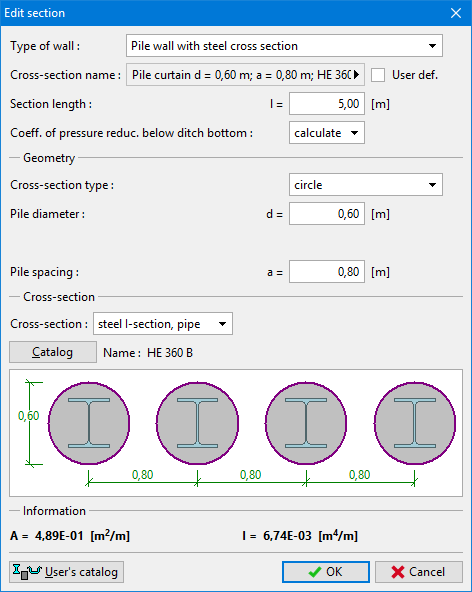
Para o cálculo das características da secção transversal, o perfil metálico é convertido em concreto.
![]()
![]()
Tubo Metálico
Um tubo metálico implica que sejam introduzidos os dados seguintes:
![]() Nome da secção transversal (é gerado um nome por defeito pelo programa, pode ser alterado através da opção “Personalizado“)
Nome da secção transversal (é gerado um nome por defeito pelo programa, pode ser alterado através da opção “Personalizado“)
![]() Coeficiente de redução de preção abaixo do fundo da vala – este coeficiente é utilizado para redução das pressões abaixo do fundo da vala para o cálculo de contenções escoradas – pode ser introduzido ou calculado automaticamente (para contenções clássicas não escoradas este coeficiente é igual a 1.0)
Coeficiente de redução de preção abaixo do fundo da vala – este coeficiente é utilizado para redução das pressões abaixo do fundo da vala para o cálculo de contenções escoradas – pode ser introduzido ou calculado automaticamente (para contenções clássicas não escoradas este coeficiente é igual a 1.0)
![]() Comprimento da secção l
Comprimento da secção l
![]() Espaçamento entre perfis a
Espaçamento entre perfis a
![]() Fator de correção para o concreto Kc (tubos enchidos com concreto)
Fator de correção para o concreto Kc (tubos enchidos com concreto)
![]() Tipo da Secção transversal, selecionado na caixa de diálogo “Catálogo de perfis” (botão “Catálogo“)
Tipo da Secção transversal, selecionado na caixa de diálogo “Catálogo de perfis” (botão “Catálogo“)
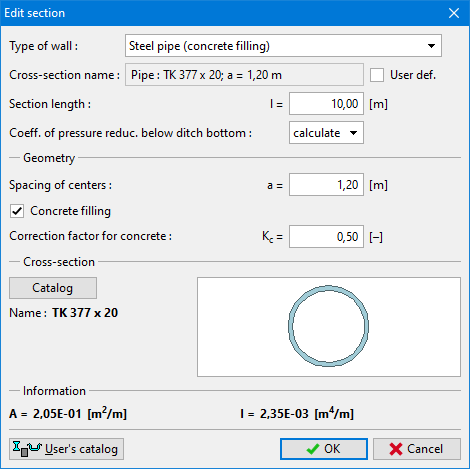
Para o cálculo das características da secção transversal de tubos metálicos enchidos com concreto, a secção metálica é convertida em concreto.
![]()
![]()
Secções Definidas pelo Usuário
No caso de se pretender uma secção personalizada, é necessário introduzir os valores das propriedades da seção (A,I) e do material (E,G).
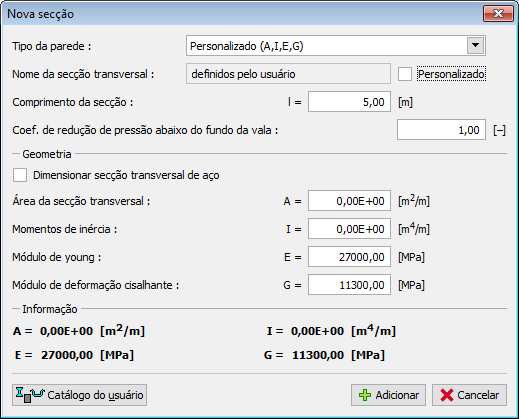
No caso da verificação de secções metálicas (função “Verificar secção transversal“) é necessário introduzir o valor do módulo seccional (W). Os parâmetros do material (E, G) são transferidos a partir da janela “Material“.
A secção transversal pode ser verificada apenas para flexão e compressão.
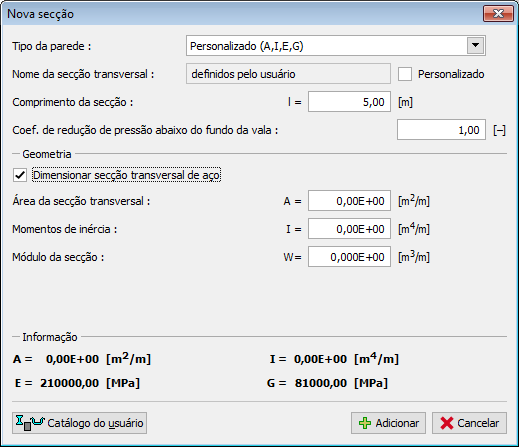
Catálogo do Usuário
O catálogo de usuário permite definir e guardar secções transversais personalizadas e as suas características, utilizadas em estruturas de contenções. Na primeira vez que o catálogo for aberto (antes de este ser criado), o programa emite uma mensagem de alerta a informar que o catálogo não foi encontrado. Ao clicar no botão “OK“, abre a caixa de diálogo “Novo catálogo” que permite introduzir o nome do catálogo e guarda-lo numa localização específica, ao clicar no botão “Guardar” (a localização assumida por defeito é a pasta onde são guardados os dados do projeto).
O programa permite que o usuário crie mais do que um catálogo. O catálogo seguinte é criado ao clicar no botão “Novo” – o programa pergunta se o catálogo existente deve ser substituído (o catálogo em utilização não será eliminado!) e guardo o novo catálogo com um nome diferente. O botão “Abrir” permite carregar um catálogo personalizado existente e o botão “Salvar como” permite guardar o catálogo com um nome diferente.
O botão “Exportar TXT” permite exportar o catálogo em utilização para um ficheiro de texto.

A caixa de diálogo “Catálogo do usuário” contém uma tabela com a lista das secções transversais personalizadas. O botão “Adicionar” abre a caixa de diálogo “Novo item de catálogo” onde é possível especificar e guardar as características de uma nova secção transversal. Os botões “Modificar” e “Remover” servem para editar as secções transversais adicionadas ao catálogo.
O botão “Adotar” abre a caixa de diálogo “Novo item de catálogo” com as características da secção transversal selecionada na caixa de diálogo “Editar secção”, onde estas podem ser modificadas e guardadas.
Cálculo Automatico do Coeficiente de Redução da Pressão abaixo do Fundo da Vala
Para o cálculo automático, o coeficiente de redução da pressão abaixo do fundo da vala k [–] é determinado da seguinte forma:
![]() cortina de estacas circular (a)
cortina de estacas circular (a)

![]() cortina de estacas retangular ou secções metálicas tipo I (b)
cortina de estacas retangular ou secções metálicas tipo I (b)

Nota: Se o coeficiente k > 1, então k = 1.

Projeto de Contenções
As análises no programa “Projeto de Contenções” podem ser divididas em três grupos:
![]() Análise de paredes não ancoradas (ex.: cortina de estacas)
Análise de paredes não ancoradas (ex.: cortina de estacas)
![]() Análise de paredes ancoradas fixas
Análise de paredes ancoradas fixas
![]() Análise de paredes ancoradas simplesmente apoiadas
Análise de paredes ancoradas simplesmente apoiadas
Também é possível analisar muros tipo Berlim (contenção suportada) através deste programa.
Análise de Cortina de Estacas
As cortinas de estacas são analisadas através da abordagem corrente, que considera o efeito dos empuxos de terra. Em geral, o empuxo de terra ativo é desenvolvido atrás da estrutura, enquanto que o empuxo de terra passivo aparece à frente da estrutura.
Com base na teoria dos estados limite, o programa procura o equilíbrio da equação de momentos, através de um método iterativo:
![]()
Após alcançar este equilíbrio, o programa determina a localização do dente da parede para a qual o equilíbrio das forças de cisalhamento é possível (computação da profundidade do ponto fixo). O comprimento total da estrutura analisada é encontrado desta forma.
Ao aplicar a abordagem baseada no fator de segurança, o programa procura verificar, através de iterações, a equação seguinte:
![]()
É percetível que a distribuição de forças internas resultante desta abordagem não é muito realista. No entanto, esta abordagem é necessária em alguns países.
A computação pode ser executada através da escolha de uma pressão mínima para dimensionamento ou através da redução do empuxo passivo. Ao assumir o valor do empuxo de terra passivo, podem ser verificadas deformações na estrutura em análise, o que, normalmente, não acontece. O empuxo passivo pode atingir o valor do empuxo em repouso, em paredes sem limites de deformação, assim como qualquer valor intermédio até ao valor do empuxo passivo para a deformação total da parede (rotação aproximada de 10 mRad – isto é, deformação de 10 mm por 1 m da altura da estrutura). Assim, é razoável considerar valores reduzidos para o empuxo de terra passivo, definindo o valor do “Coeficiente de redução do empuxo passivo” como menor ou igual a um. Os seguinte valores são recomendados:
![]() 0.67 reduz as deformações para aproximadamente metade
0.67 reduz as deformações para aproximadamente metade
![]() 0.50 corresponde, aproximadamente, a deformações da estrutura carregada pelo empuxo de terra aumentado
0.50 corresponde, aproximadamente, a deformações da estrutura carregada pelo empuxo de terra aumentado
![]() 0.33 corresponde, aproximadamente, a deformações da estrutura carregada pelo empuxo em repouso, a estrutura atinge cerca de 20 % da sua deformação original
0.33 corresponde, aproximadamente, a deformações da estrutura carregada pelo empuxo em repouso, a estrutura atinge cerca de 20 % da sua deformação original
Análise de Parede Ancorada Fixa
As paredes ancoradas fixas são analisadas como vigas contínuas, com a deformação variante do método dos elementos finitos, de modo a cumprir a suposição de a parede estar fixa ao solo. A análise é precedida pela carga de deformação devido ao empuxo de terra aplicado à estrutura. O empuxo atuante na parte posterior da parede é assumido como empuxo ativo, enquanto que a face frontal é carregada por empuxo passivo.
O empuxo passivo pode ser reduzido pelo coeficiente de redução de empuxo passivo. Ao assumir o valor do empuxo de terra passivo, podem ser verificadas deformações na estrutura em análise, o que, normalmente, não acontece. O empuxo passivo pode atingir o valor do empuxo em repouso, em paredes sem limites de deformação, assim como qualquer valor intermédio até ao valor do empuxo passivo para a deformação total da parede (rotação aproximada de 10 mRad – isto é, deformação de 10 mm por 1 m da altura da estrutura). Assim, é razoável considerar valores reduzidos para o empuxo de terra passivo, definindo o valor do “Coeficiente de redução do empuxo passivo” como menor ou igual a um. Os seguinte valores são recomendados:
![]() 0.67 reduz as deformações para aproximadamente metade
0.67 reduz as deformações para aproximadamente metade
![]() 0.33 corresponde, aproximadamente, a deformações de cerca de 20 % da sua deformação original
0.33 corresponde, aproximadamente, a deformações de cerca de 20 % da sua deformação original
O programa oferece duas opções para determinar o empuxo ativo:
![]() calcular os parâmetros introduzidos para o solo, nível freático, sobrecargas, terreno, incluindo a introdução da pressão mínima para dimensionamento
calcular os parâmetros introduzidos para o solo, nível freático, sobrecargas, terreno, incluindo a introdução da pressão mínima para dimensionamento
![]() inserir uma distribuição de empuxo de terra até à profundidade do ponto de valor zero (desta forma é possível introduzir uma redistribuição do empuxo de terra)
inserir uma distribuição de empuxo de terra até à profundidade do ponto de valor zero (desta forma é possível introduzir uma redistribuição do empuxo de terra)
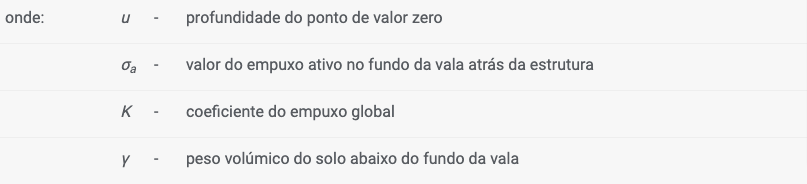
O ponto de valor zero, isto é, o ponto para o qual o empuxo global é nulo, é determinado através da seguinte expressão:
![]()
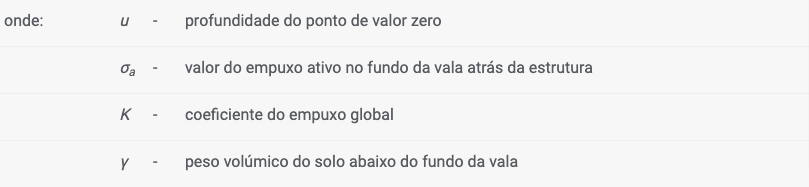
A análise da estrutura fixa assuma que o ponto de carga nula N (à profundidade u) é idêntico ao ponto de momento nulo. Para esta análise, a estrutura é dividida em duas partes – uma parte superior (viga superior) até ao ponto de valor zero e uma parte inferior:
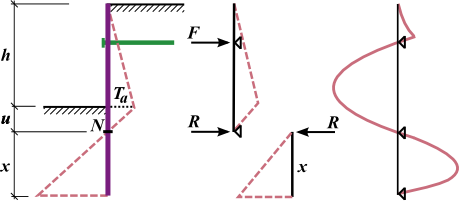
A viga superior é analisada juntamente com a avaliação das forças de ancoragem F e da força de reação R no ponto de valor zero. Seguidamente, o comprimento x da viga inferior é determinado de forma a que a condição do equilíbrio de momentos seja satisfeita (a viga é carregada pela reação R e pela diferença dos empuxos de terra). Para satisfazer o equilíbrio da força de cisalhamento, o comprimento fixo computado é aumentado pelo valor Δx, conforme mostra a figura:
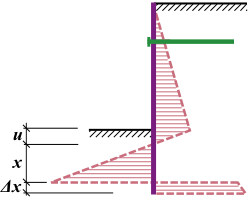
Análise de Parede Ancorada Simplesmente Apoiada
As paredes ancoradas simplesmente apoiadas são analisadas como vigas contínuas, com a deformação variante do método dos elementos finitos, de modo a cumprir a suposição de a parede estar fixa ao solo. A análise é precedida pela carga de deformação devido ao empuxo de terra aplicado à estrutura. O empuxo atuante na parte posterior da parede é assumido como empuxo ativo, enquanto que a face frontal é carregada por empuxo passivo.
O empuxo passivo pode ser reduzido pelo coeficiente de redução de empuxo passivo. Ao assumir o valor do empuxo de terra passivo, podem ser verificadas deformações na estrutura em análise, o que, normalmente, não acontece. O empuxo passivo pode atingir o valor do empuxo em repouso, em paredes sem limites de deformação, assim como qualquer valor intermédio até ao valor do empuxo passivo para a deformação total da parede (rotação aproximada de 10 mRad – isto é, deformação de 10 mm por 1 m da altura da estrutura). Assim, é razoável considerar valores reduzidos para o empuxo de terra passivo, definindo o valor do “Coeficiente de redução do empuxo passivo” como menor ou igual a um. Os seguinte valores são recomendados:
![]() 0.67 reduz as deformações para aproximadamente metade
0.67 reduz as deformações para aproximadamente metade
![]() 0.33 corresponde, aproximadamente, a deformações de cerca de 20 % da sua deformação original
0.33 corresponde, aproximadamente, a deformações de cerca de 20 % da sua deformação original
O programa oferece duas opções para determinar o empuxo ativo:
![]() calcular os parâmetros introduzidos para o solo, nível freático, sobrecargas, terreno, incluindo a introdução da pressão mínima para dimensionamento
calcular os parâmetros introduzidos para o solo, nível freático, sobrecargas, terreno, incluindo a introdução da pressão mínima para dimensionamento
![]() inserir uma distribuição de empuxo de terra até à profundidade do ponto de valor zero (desta forma é possível introduzir uma redistribuição do empuxo de terra)
inserir uma distribuição de empuxo de terra até à profundidade do ponto de valor zero (desta forma é possível introduzir uma redistribuição do empuxo de terra)
O ponto de valor zero, isto é, o ponto para o qual o empuxo global é nulo, é determinado através da seguinte expressão:
![]()
Para estruturas simplesmente apoiadas, assume-se que o momento e força de cisalhamento são nulos no apoio. O programa define a posição do ponto fixo da estrutura no ponto de valor zero e, seguidamente, procura a localização x do final da viga, onde a condição acima é verificada (ver figura). O procedimento para paredes com ancoragens múltiplas é idêntico.
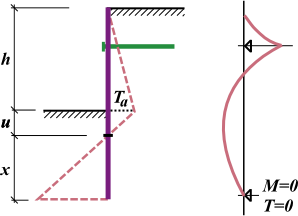
Verificação de Contenções
O programa verifica a estrutura introduzida através do método de pressões dependentes ou do método de mola de acordo com JGJ 120-2012. A carga aplicada à estrutura é derivada da sua deformação, que permite modelar o seu comportamento de forma realista realista e permite dimensionamentos económicos. A análise considera o processo construtivo como etapas individuais da construção progressiva da parede (etapas de construção), incluindo a evolução gradual das deformações e ancoragens pós-tensionadas. O programa também pode modelar qualquer tipo de contenção suportada.
A utilização do método de pressões dependentes implica a determinação do módulo de reação do subsolo, que pode ser assumido como linear ou não linear.
O programa também permite que o usuário verifique a estabilidade interna do sistema de ancoragem.
A análise é realizada com recurso à variação da deformação do método dos elementos finitos. Deslocamentos, forças internas e módulo de reação do subsolo são avaliados para cada nó.
É assumido o seguinte procedimento para dividir a estrutura em elementos finitos:
![]() Primeiro, os nós são inseridos em todos os pontos topológicos da estrutura (pontos de origem e fim, pontos de localização de ancoragens, pontos de remoção de solo, pontos de mudança de secção transversal).
Primeiro, os nós são inseridos em todos os pontos topológicos da estrutura (pontos de origem e fim, pontos de localização de ancoragens, pontos de remoção de solo, pontos de mudança de secção transversal).
![]() Com base na subdivisão obtida, o programa computa os nós restantes de forma a que todos os elementos apresentem, aproximadamente, tamanho semelhante.
Com base na subdivisão obtida, o programa computa os nós restantes de forma a que todos os elementos apresentem, aproximadamente, tamanho semelhante.
É atribuído a cada elemento um valor para o módulo de reação do subsolo. Os apoios são introduzidos na estrutura deformada – cada apoio representa um deslocamento forçado aplicado à estrutura.
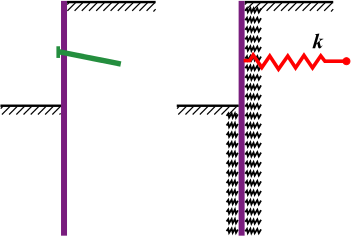
Na etapa de construção em que as ancoragens pré-tensionadas são inseridas, estas são modeladas como forças (variante I da figura). Nas outras etapas de construção, as ancoragens são modeladas como molas de rigidez k (variante II da figura) e forças:

Ancoragens não pré-tensionadas são sempre modeladas como molas, em todas as etapas de construção. A força da ancoragem é computada a partir da estrutura e da rigidez da ancoragem:
A variação da força de ancoragem devido à deformação é dada por:
![]()
![]()

Bibliografia:
Hurych, P.: Metoda zavislych tlaku. Sbornik konference “Automatizacia projektovania”, Vysoke Tatry, 1978.
Tipos de Ancoragens
O programa permite selecionar ancoragens pré-tensionadas ou não pré-tensionadas e calcular a sua capacidade de suporte.
Se a verificação da ancoragem não for necessária, o tipo de ancoragem selecionado pode ser “não definido“. Neste caso, apenas é introduzida informação necessária para a análise global da estrutura (geometria, rigidez).
O programa permite selecionar os seguintes tipos de ancoragem:
![]() barras pré-tensionadas
barras pré-tensionadas
![]() strand
strand
![]() helicoidal
helicoidal
![]() barras não pré-tensionadas
barras não pré-tensionadas
![]() deadman
deadman
As ancoragens podem ser verificadas para três tipos de falha diferentes.
![]() Resistência da arrancamento Rt (todos os tipos)
Resistência da arrancamento Rt (todos os tipos)
![]() Resistência de arrancamento (solo) Re (barras e strand)
Resistência de arrancamento (solo) Re (barras e strand)
![]() Resistência de arrancamento (argamassa) Rc (barras pré-tensionadas e strand)
Resistência de arrancamento (argamassa) Rc (barras pré-tensionadas e strand)
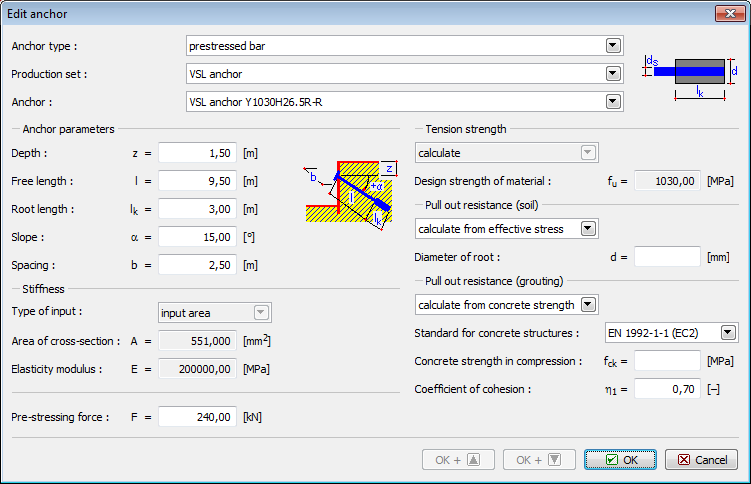
Barras Pré-tensionadas
As “Barras pré-tensionadas” podem ser selecionadas como um “Tipo de ancoragem” da lista na caixa de diálogo “Nova ancoragem“.
As barras pré-tensionadas implicam a introdução de:
![]() Linha de fabricação – definido pelo usuário (parâmetros introduzidos pelo usuário) ou a partir do catálogo (VSL, DYWIDAG…)
Linha de fabricação – definido pelo usuário (parâmetros introduzidos pelo usuário) ou a partir do catálogo (VSL, DYWIDAG…)
![]() Localização da ancoragem – profundidade, comprimento, comprimento ancorado, inclinação…
Localização da ancoragem – profundidade, comprimento, comprimento ancorado, inclinação…
![]() Rigidez da ancoragem – diâmetro da ancoragem ds ou área da ancoragem A, módulo de elasticidade E
Rigidez da ancoragem – diâmetro da ancoragem ds ou área da ancoragem A, módulo de elasticidade E
![]() Força de pré-tensionamento
Força de pré-tensionamento
![]() Parâmetros para verificação da ancoragem (Resistência da arrancamento, Resistência de arrancamento (solo), Resistência de arrancamento (argamassa))
Parâmetros para verificação da ancoragem (Resistência da arrancamento, Resistência de arrancamento (solo), Resistência de arrancamento (argamassa))
Bibliografia:
Ancoragens implementadas no catálogo
![]() VSL Systems Ltd. – VSL Ground Anchor Systems – web brochure
VSL Systems Ltd. – VSL Ground Anchor Systems – web brochure
![]() Dywidag- Systems International – Dywidag Bar Anchors, Dywidag Strand anchors – web brochures
Dywidag- Systems International – Dywidag Bar Anchors, Dywidag Strand anchors – web brochures
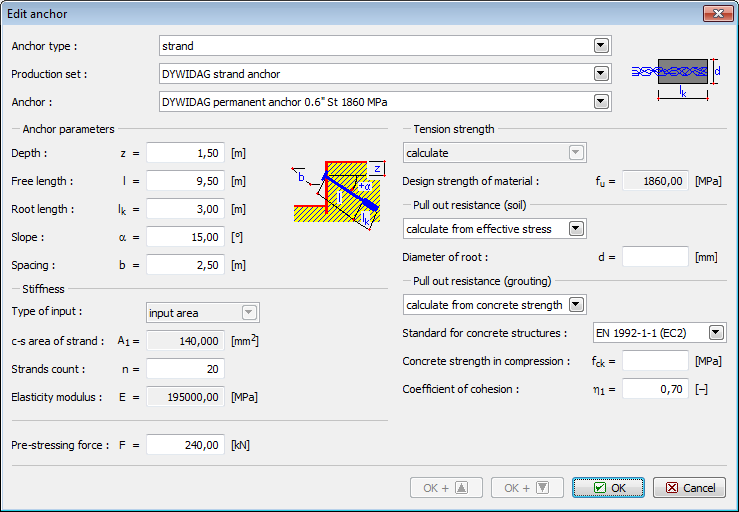
Ancoragens Strand
As “Ancoragens strand” podem ser selecionadas como um “Tipo de ancoragem” da lista na caixa de diálogo “Nova ancoragem“.
As ancoragens strand implicam a introdução de:
![]() Linha de fabricação – definido pelo usuário (parâmetros introduzidos pelo usuário) ou a partir do catálogo (VSL, DYWIDAG…)
Linha de fabricação – definido pelo usuário (parâmetros introduzidos pelo usuário) ou a partir do catálogo (VSL, DYWIDAG…)
![]() Localização da ancoragem – profundidade, comprimento, comprimento ancorado, inclinação…
Localização da ancoragem – profundidade, comprimento, comprimento ancorado, inclinação…
![]() Rigidez da ancoragem – diâmetro strand d1 (ou área strand A1), número de strands n e módulo de elasticidade E
Rigidez da ancoragem – diâmetro strand d1 (ou área strand A1), número de strands n e módulo de elasticidade E
![]() Força de pré-tensionamento
Força de pré-tensionamento
![]() Parâmetros para verificação da ancoragem (Resistência da arrancamento, Resistência de arrancamento (solo), Resistência de arrancamento (argamassa))
Parâmetros para verificação da ancoragem (Resistência da arrancamento, Resistência de arrancamento (solo), Resistência de arrancamento (argamassa))
Bibliografia:
Ancoragens implementadas no catálogo
![]() VSL Systems Ltd. – VSL Ground Anchor Systems – web brochure
VSL Systems Ltd. – VSL Ground Anchor Systems – web brochure
![]() Dywidag- Systems International – Dywidag Bar Anchors, Dywidag Strand anchors – web brochures
Dywidag- Systems International – Dywidag Bar Anchors, Dywidag Strand anchors – web brochures
Ancoragens Helicoidais
As “Ancoragens helicoidais” podem ser selecionadas como um “Tipo de ancoragem” da lista na caixa de diálogo “Nova ancoragem“.
As ancoragens helicoidais implicam a introdução de:
![]() Linha de fabricação – definido pelo usuário (parâmetros introduzidos pelo usuário) ou a partir do catálogo (Helical Anchors, Mac Lean, Chance…). As ancoragens do catálogo são especificadas por parâmetros diferentes (tipo de poço, número de hélices, espessura e material da hélice) – se a combinação selecionada não for fabricada, o nome da ancoragem não é preenchido e a edição não pode ser realizada
Linha de fabricação – definido pelo usuário (parâmetros introduzidos pelo usuário) ou a partir do catálogo (Helical Anchors, Mac Lean, Chance…). As ancoragens do catálogo são especificadas por parâmetros diferentes (tipo de poço, número de hélices, espessura e material da hélice) – se a combinação selecionada não for fabricada, o nome da ancoragem não é preenchido e a edição não pode ser realizada
![]() Localização da ancoragem – profundidade, comprimento, inclinação…
Localização da ancoragem – profundidade, comprimento, inclinação…
![]() Tipo de poço – circular, quadrangular
Tipo de poço – circular, quadrangular
![]() Rigidez da ancoragem – módulo de elasticidade E
Rigidez da ancoragem – módulo de elasticidade E
![]() Parâmetros para verificação da ancoragem (Resistência da arrancamento, Resistência de arrancamento (solo) descrito abaixo)
Parâmetros para verificação da ancoragem (Resistência da arrancamento, Resistência de arrancamento (solo) descrito abaixo)
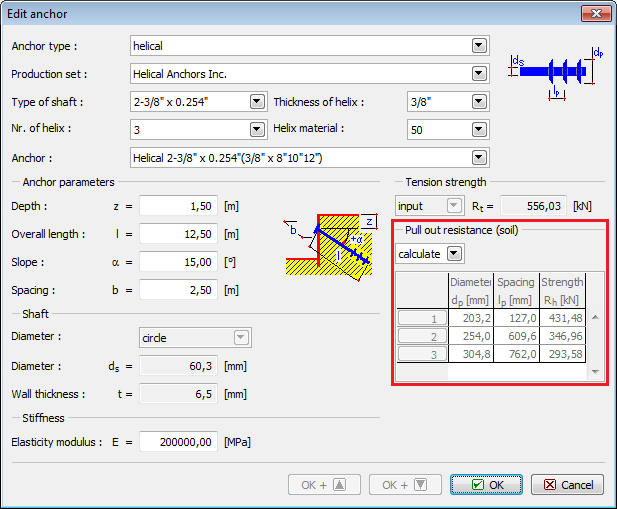
Cálculo da resistência de arrancamento do solo:
Opção “introduzir“
Esta opção é necessária para ancoragens definidas pelo usuário. É necessário introduzir o valor da resistência de arrancamento do solo Re [kN, lbf]. A tabela com a dimensão e localização de cada hélice serve apenas para visualizar as ancoragens e verificar a estabilidade interna.
Opção “calcular“
Esta opção apenas está disponível para ancoragens do catálogo. A dimensão e localização de cada hélice é determinada pelo fabricante. A resistência à remoção do solo é calculada de acordo com a fórmula seguinte:
![]()
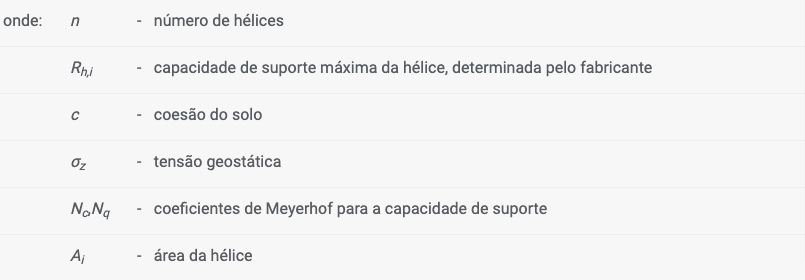
![]()
![]()
Bibliografia:
Ancoragens implementadas no catálogo
![]() Helical Anchors, Inc. – Product Catalog
Helical Anchors, Inc. – Product Catalog
![]() MacLean-Dixie – Helical Foundation Syastems – Engineering Reference Manual
MacLean-Dixie – Helical Foundation Syastems – Engineering Reference Manual
![]() Chance – Civil Construction Product Catalog, Vol. I.
Chance – Civil Construction Product Catalog, Vol. I.
Barras Não Pré-tensionadas
As “Barras não pré-tensionadas” podem ser selecionadas como um “Tipo de ancoragem” da lista na caixa de diálogo “Nova ancoragem“.
As barras não pré-tensionadas implicam a introdução de:
![]() Linha de fabricação – definido pelo usuário (parâmetros introduzidos pelo usuário) ou a partir do catálogo (VSL, DYWIDAG…)
Linha de fabricação – definido pelo usuário (parâmetros introduzidos pelo usuário) ou a partir do catálogo (VSL, DYWIDAG…)
![]() Localização da ancoragem – profundidade, comprimento, inclinação…
Localização da ancoragem – profundidade, comprimento, inclinação…
![]() Rigidez da ancoragem – diâmetro da ancoragem ds ou área da ancoragem A, módulo de elasticidade E
Rigidez da ancoragem – diâmetro da ancoragem ds ou área da ancoragem A, módulo de elasticidade E
![]() Parâmetros para verificação da ancoragem (Resistência da arrancamento, Resistência de arrancamento (solo))
Parâmetros para verificação da ancoragem (Resistência da arrancamento, Resistência de arrancamento (solo))
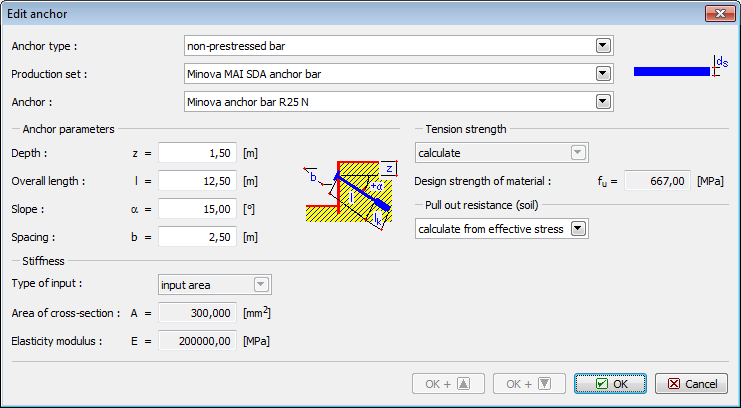
Bibliografia:
Ancoragens implementadas no catálogo
![]() VSL Systems Ltd. – VSL Ground Anchor Systems – web brochure
VSL Systems Ltd. – VSL Ground Anchor Systems – web brochure
![]() Minova Bohemia, s.r.o. – Injekční zavrtávací a kotevní tyče MAI SDA R a T, Technický list
Minova Bohemia, s.r.o. – Injekční zavrtávací a kotevní tyče MAI SDA R a T, Technický list
Ancoragens Deadman
As “Ancoragens deadman” podem ser selecionadas como um “Tipo de ancoragem” da lista na caixa de diálogo “Nova ancoragem“.
As ancoragens deadman implicam a introdução de:
![]() Localização da ancoragem – profundidade, comprimento, espaçamento
Localização da ancoragem – profundidade, comprimento, espaçamento
![]() Rigidez da ancoragem – diâmetro da ancoragem ds ou área da ancoragem A, módulo de elasticidade E
Rigidez da ancoragem – diâmetro da ancoragem ds ou área da ancoragem A, módulo de elasticidade E
![]() Parâmetros para verificação da ancoragem (Resistência da arrancamento, Resistência de arrancamento (solo) descrito abaixo)
Parâmetros para verificação da ancoragem (Resistência da arrancamento, Resistência de arrancamento (solo) descrito abaixo)
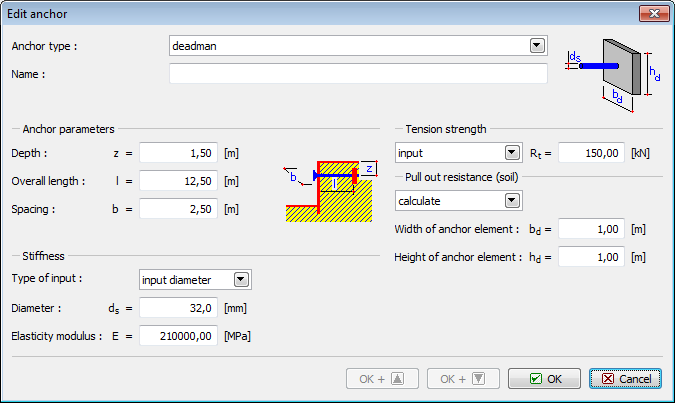
Análise de ancoragens deadman
A ancoragem deadman consiste numa barra com comprimento definido e um elemento de ancoragem.
A resistência de arrancamento do solo é igual à resistência passiva ao longo do elemento de ancoragem, a qual é reduzida pelo coeficiente k:
![]()
Para h = 0:
![]()
Para h ≥ b – bD:
![]()

O coeficiente k é interpolado para os valores intermédios de h.
A saliência sobre o elemento de ancoragem é calculado através de:
![]()
A resistência ao arrancamento total é ativada se as cunhas de terra ativas e passivas não se intersetarem.
O comprimento mínimo da barra para a resistência ao arrancamento é computada através de:
![]()

Caso o comprimento da barra l seja inferior ao comprimento mínimo da barra lmin, o empuxo passivo é considerado desde a interseção das cunhas de terra ativa e passiva.
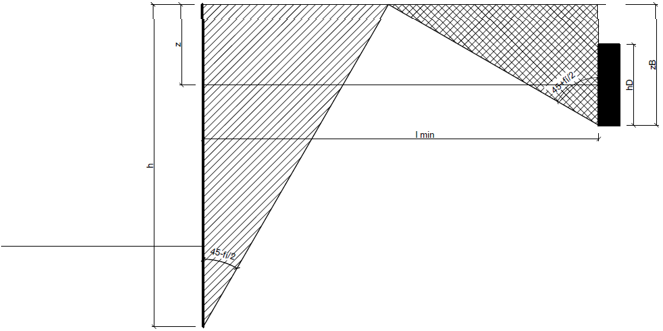
Resistência de Arrancamento
O método de análise é selecionado na secção “Resistência de arrancamento“.
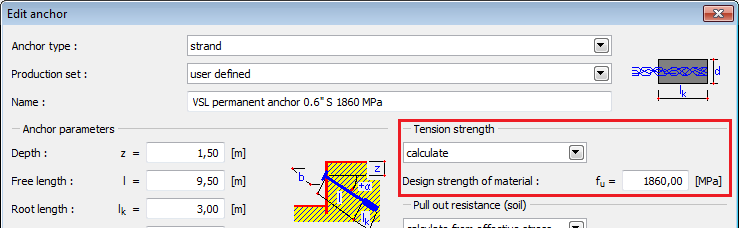
Opção “calcular“
O cálculo é igual para todos os tipos de ancoragens, conforme a fórmula seguinte:
![]()

Opção “introduzir“
É necessário introduzir o valor da resistência de arrancamento Rt [kN, lbf].
Para ancoragens strand, é necessário introduzir a área de um strand (opção “inserir área“) – a área total é calculada de acordo com a fórmula:
![]()

No caso de ser inserido o diâmetro do strand (opção “inserir diâmetro“), a área total é calculada de acordo com a fórmula seguinte:
![]()

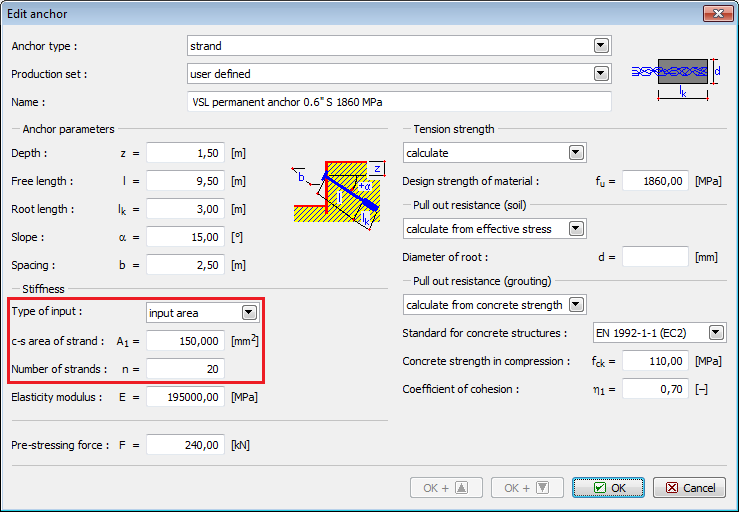
Resistência de Arrancamento (Solo)
O método de análise é selecionado na secção “Resistência de arrancamento (solo)“.
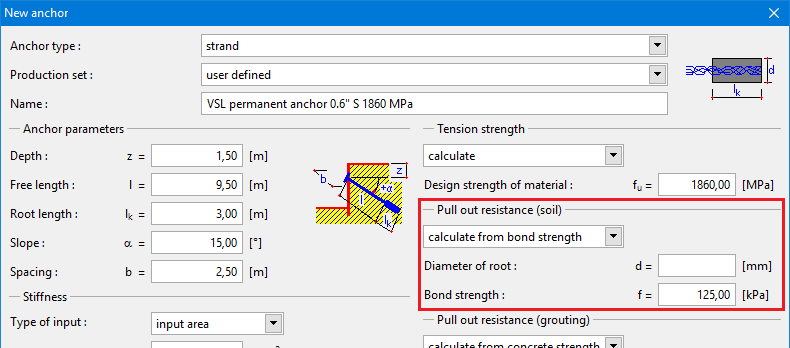
Análise para barras pré-tensionadas, strand e não pré-tensionadas
Opção “cálculo da tensão efetiva”
![]()
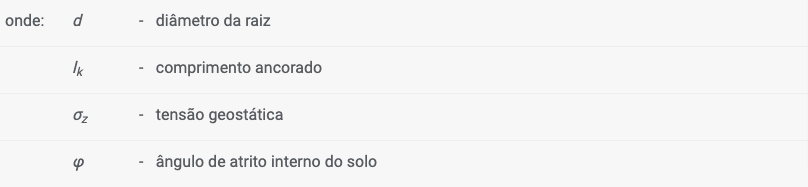
Opção “cálculo do atrito superficial”
![]()

Opção “introduzir capacidade de suporte por unidade de comprimento”
![]()

Opção “introduzir”
O valor total da resistência de arrancamento (solo) é inserido em Re [kN, lbf].
Resistência de Arrancamento (Argamassa)
O método de análise é selecionado na secção “Resistência de arrancamento (argamassa)“.
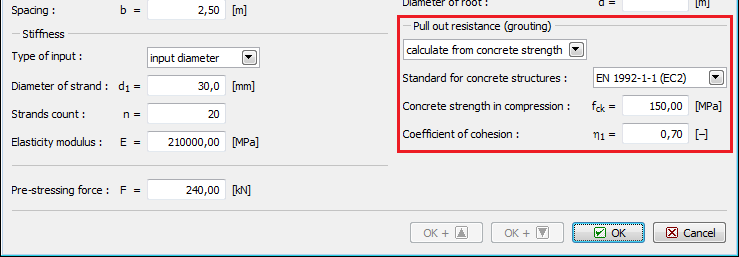
Esta capacidade de suporte determina a resistência ao arrancamento da raiz e é calculada de igual forma para barras pré-tensionadas e ancoragens strand.
![]()
Opção “cálculo da força de cisalhamento”

Opção “cálculo da força do concreto”
A análise é a mesma que para o caso anterior, a força de cisalhamento τ é calculada a partir dos parâmetros do concreto de acordo com as diferentes Normas:
![]() EN 1992-1-1 (EC2)
EN 1992-1-1 (EC2)
![]()

![]() ACI 318-11
ACI 318-11
![]()
![]()
![]() GB 50010-2010
GB 50010-2010
![]()
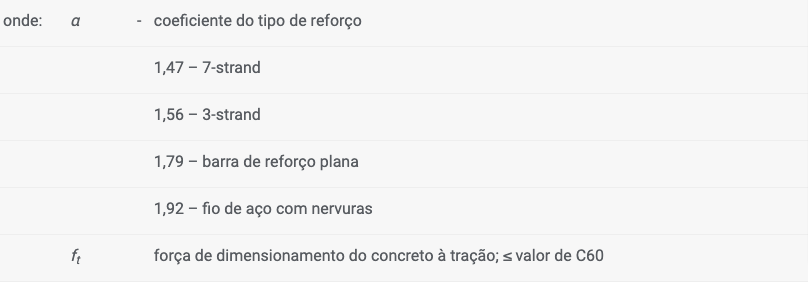
Opção “introduzir capacidade de suporte por unidade de comprimento”
![]()

Opção “introduzir”
O valor total da resistência de arrancamento (solo) é inserido em Re [kN, lbf].
Apoios – Carregamentos devido a Variações de Temperatura
Os apoios podem ser carregados por uma variação de temperatura uniforme. A sua definição implica um coeficiente de expansão térmica αt e uma variação de temperatura Δt entre a etapa de construção atual e seguinte.
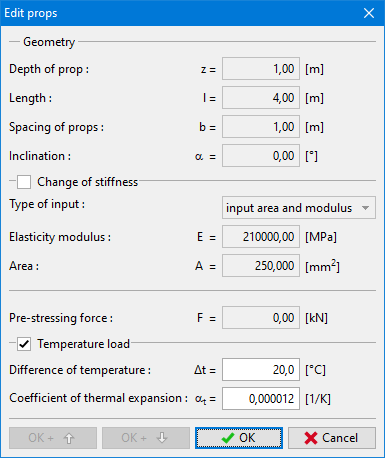
O valor da força adicional no apoio devido a uma variação de temperatura é dada por:
![]()
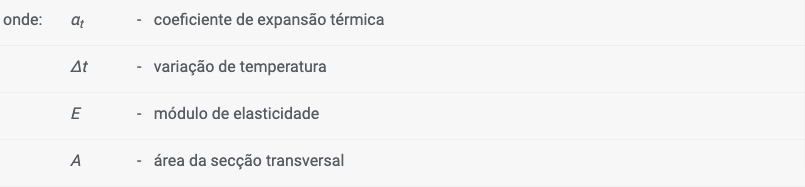
Método das Pressões Dependentes
A suposição base deste método é que o solo, ou rocha, na vizinhança da parede, assume um comportamento elasto-plástico de Winkler ideal. Este material é determinado pelo módulo de reação do subsolo kh, que caracteriza a deformação na região elástica e as deformações limitadas adicionais. Ao exceder estas deformações, o material assume um comportamento plástico ideal.
As seguintes premissas são utilizadas:
![]() O empuxo atuante na parede pode assumir um valor qualquer, entre os valores do empuxo ativo e passivo – mas nunca pode exceder estes limites.
O empuxo atuante na parede pode assumir um valor qualquer, entre os valores do empuxo ativo e passivo – mas nunca pode exceder estes limites.
![]() O empuxo em repouso atua numa estrutura não deformada (w = 0).
O empuxo em repouso atua numa estrutura não deformada (w = 0).
O empuxo atuante numa estrutura deformada é dado por:
![]()
σ = σa para: σ < σa
σ = σp para: σ > σp
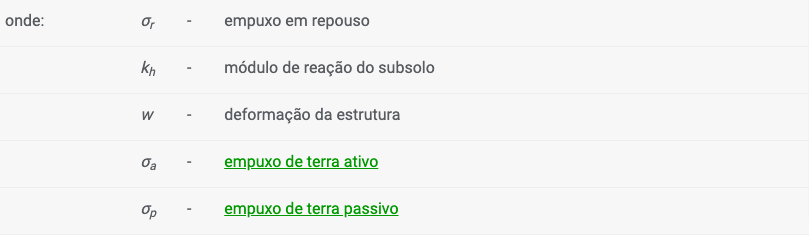
O procedimento computacional segue os passos seguintes:
![]() O módulo de reação do subsolo kh é atribuído a todos os elementos e a estrutura é carregada pelo empuxo em repouso – ver figura:
O módulo de reação do subsolo kh é atribuído a todos os elementos e a estrutura é carregada pelo empuxo em repouso – ver figura:
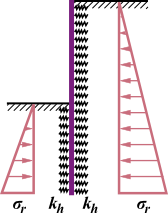
![]() A análise continua com a verificação da condição dos limites dos valores dos empuxos atuantes na parede. Nas zonas em que esta condição não for cumprida, o programa atribui o valor kh = 0 e a parede é carregada por empuxos ativos ou passivos – ver figura:
A análise continua com a verificação da condição dos limites dos valores dos empuxos atuantes na parede. Nas zonas em que esta condição não for cumprida, o programa atribui o valor kh = 0 e a parede é carregada por empuxos ativos ou passivos – ver figura:
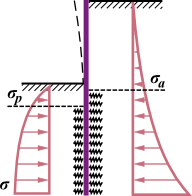
O processo iterativo continua até que todas as condições sejam verificadas.
Na análise das etapas seguintes, o programa considera que a parede sofre deformações plásticas. Esta é uma das razões para definir etapas de construção individuais, de acordo com o processo construtivo real.
Bibliografia:
Bartak, J.: Progresivni postupy navrhovani pazenych stavebnich jam. VUT Brno, 1991.
Hurych, P.: Metoda zavislych tlaku. Sbornik konference “Automatizacia projektovania”, Vysoke Tatry, 1978.
Módulo de Reação do Subsolo
O programa apresenta as seguintes opções para introduzir o módulo de reação do subsolo:
![]() na forma de distribuição (a distribuição do módulo de reação do subsolo kh é introduzida à frente e atrás da estrutura)
na forma de distribuição (a distribuição do módulo de reação do subsolo kh é introduzida à frente e atrás da estrutura)
![]() como parâmetro do solo com um valor respetivo (curva linear ou não linear)
como parâmetro do solo com um valor respetivo (curva linear ou não linear)
![]() de acordo com Schmitt
de acordo com Schmitt
![]() de acordo com Chadeisson
de acordo com Chadeisson
![]() de acordo com CUR 166
de acordo com CUR 166
![]() através de iterações, pela deformação característica dos solos
através de iterações, pela deformação característica dos solos
![]() na introdução de resultados do ensaio pressiométrico (PMT) (de acordo com NF P 94-282, segundo Menard)
na introdução de resultados do ensaio pressiométrico (PMT) (de acordo com NF P 94-282, segundo Menard)
![]() na introdução de resultados do ensaio dilatométrico (DMT)
na introdução de resultados do ensaio dilatométrico (DMT)
![]() de acordo com as Normas Chinesas (métodos “c”, “k” ou “m”)
de acordo com as Normas Chinesas (métodos “c”, “k” ou “m”)
O módulo de reação horizontal do subsolo corresponde, geralmente, à rigidez da mola segundo o modelo de Winkler, que descreve a relação entre a carga aplicada a uma laje rígida e a deformação resultante do solo, dado pela fórmula:
![]()

Módulo de Reação do Subsolo segundo Schmitt
Esta análise do módulo de reação do subsolo assenta na relação entre o módulo edométrico e a rigidez na flexão da estrutura segundo Schmitt, em Revue Francaise de Géotechnique no. 71 e 74:
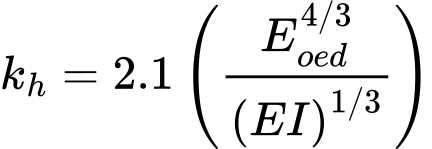

Biliografia:
K. J. Bakker, A. Bezuijen, W. Broere, E. A. Kwast: Geotechnical Aspects of Underground Construction in Soft Ground: Proceedings of the 5th International Symposium TC28. Amsterdam, the Netherlands, 15-17 June 2005. CRC Press, 2013, pp. 616, ISBN: 0415889138, 9780415889131.
Monnet, A.: Module de réaction, coefficient de décompression, au sujet des paramètres utilisés dans la méthode de calcul élastoplastique, Revue française de Géotechnique, 65, 1994, pp. 67 – 72.
Mitew, M.: Numerical analysis of displacements of a diaphragm wall. Warsaw University of Technology, Poland.
N. M. ILIEŞ, T. A. HULPUȘ, A. POPA: Design of Anchored Walls: The Influence of Design Approaches and Design Methods. Technical University of Cluj Napoca, Faculty of Civil Engineering, Romania, 2010.
Módulo de Reação do Subsolo segundo Chadeisson
Baseia-se em medições de estruturas de contenções em diferentes solos e na computação de deslocamentos da estrutura necessários para mobilizar o valor limite do empuxo passivo, segundo R. Chadeisson (1961) e A. Monnet (1994), derivado da expressão para determinação do módulo de reação do subsolo:
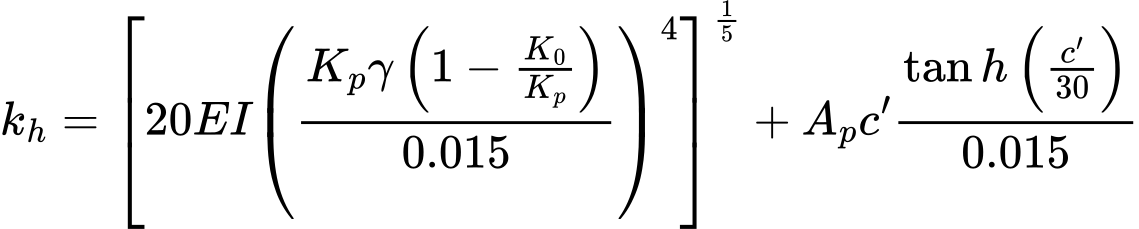

Este método não está disponível para estruturas de estacas-prancha de plástico.
Bibliografia:
Schmitt, P. (1995): “Estimating the coefficient of subgrade reaction for diaphragm wall and sheet pile wall design”, in French. Revue Française de Géotechnique, N. 71, 2° trimestre 1995, 3-10.
Módulo de Reação do Subsolo segundo CUR 166
A seguinte tabela contém os valores para o módulo de reação do subsolo, obtidos através de ensaios experimentais realizados na Holanda (descrito em CUR 166). A tabela contém módulos secantes, que o programa transforma automaticamente em módulos secantes da reação do subsolo – ver módulo não linear de reação do subsolo.
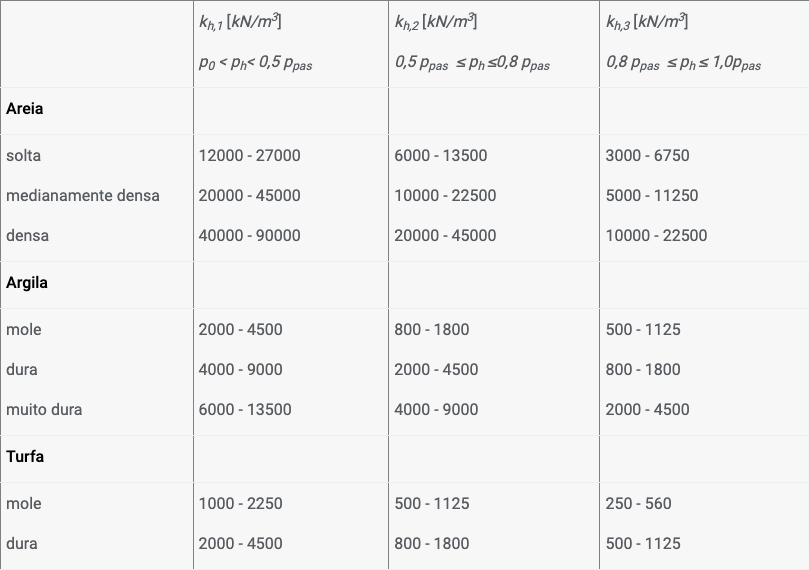

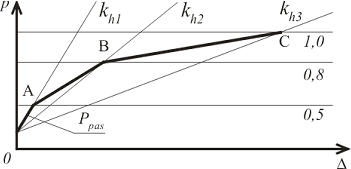
Bibliografia:
CUR 166 Damwandconstructies, available at Civieltechnisch Centrum Uitvoering Research en Regelgeving: P.O.Box 420, 2800 AK Gouda (NL).
Módulo de Reação do Subsolo determinado a partir de Iterações
O programa permite o cálculo automático do módulo de reação do subsolo a partir da deformação característica do solo, através de um processo iterativo. O procedimento assenta na suposição de que a deformação de solos elásticos, caracterizados pelo módulo de deformação Edef [MPa], ao alterar o estado de tensões associado à alteração de empuxos, é a mesma que a deformação da parede subterrânea.
O objetivo é encontrar os valores de kh [MN/m3] que permitam a continuidade das deformações da parede e solo adjacente. A deformação plástica da estrutura não é considerada ao realizar a análise com a iteração manual de kh. Enquanto que para a análise de iteração automática da deformação plástica da estrutura, o módulo kh é considerado. O princípio da iteração manual consiste na computação do módulo de reação do subsolo do iésimo segmento da parede livre de ancoragem, conforme representado esquematicamente na figura:
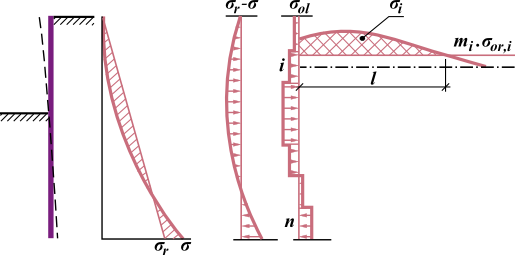
Para alterar a tensão σr – σ, o programa determina a carga uniforme σol [MPa] de cada segmento da estrutura. Seguidamente, a alteração global da tensão que atravessa o iésimo segmento (![]() [MPa*m]) é computada. Esta alteração deve-se à carga adicional do subsolo nos segmentos 1 a n (σol,1 – σol,n). A alteração global da tensão Δσi é reduzida pela robustez estrutural mi*σor,i [MPa]. O novo valor da rigidez da mola é dado por:
[MPa*m]) é computada. Esta alteração deve-se à carga adicional do subsolo nos segmentos 1 a n (σol,1 – σol,n). A alteração global da tensão Δσi é reduzida pela robustez estrutural mi*σor,i [MPa]. O novo valor da rigidez da mola é dado por:
![]()

A alteração da tensão no subsolo é determinada de acordo com Boussinesque. Inserir o novo valor de k diretamente no cálculo seguinte poderia levar a uma iteração instável – assim, o valor de k que é introduzido na análise da parede seguinte é determinado a partir do valor original de kp e do novo valor de kn do módulo de reação do subsolo.
![]()

O valor máximo do módulo de reação do subsolo da iésima camada é limitado por:
![]()
O processo iterativo manual, utilizado para computar o módulo de reação do subsolo, segue os passos seguintes:
- Determinar a matriz de valores influentes para derivar a alteração da tensão para uma profundidade do subsolo que atravessa o iésimo segmente da estrutura devido à sobrecarga causada pela alteração da tensão em outros segmentos.
- Introduzir a primeira aproximação do módulo kh à frente da parede – é assumida uma distribuição triangular de valores na base da parede kh = 10 MN/m3.
- Executar a análise da parede (estrutura de contenção).
- Computar os novos valores de kh e determinar os novos valores para a análise seguinte.
- A caixa de diálogo para verificar a interação aparece e o programa aguarda pelo próximo comando. Se as n iterações seguintes forem selecionadas, os passos 3 e 4 repetem-se n vezes até chegar ao passo nº 5, novamente. A análise pode ser finalizada a partir da caixa de diálogo, ao clicar no botão “Terminar“.
Este processo iterativo manual é controlado pelo usuário – o usuário pode decidir se os resultados são realistas. O processo iterativo automático é executado sem serem inseridas novas interações para o cálculo do módulo kh.
Bibliografia:
Bartak J.: Progresivni postupy navrhovani pazenych stavebnich jam, VUT Brno, 1991.
Módulo de Reação do Subsolo segundo Menard
Baseia-se nos resultados de medições experimentais (pressiómetro) da resposta do solo carregado pela laje rígida de Menard, de acordo com a seguinte expressão para o módulo de reação do subsolo:
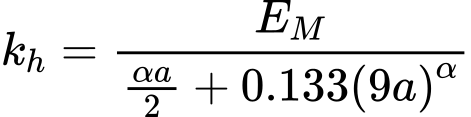

Valores aproximados para o coeficiente reológico do solo α
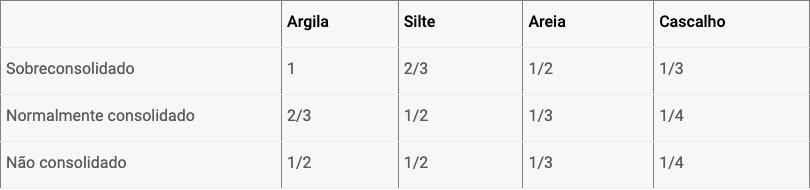
Bibliografia:
Menard, L. (1975): “The Menard Pressuremeter: Interpretation and Application of the Pressuremeter Test Results to Foundations Design”, Sols-Soils, No. 26, Paris, France.
Módulo de Reação do Subsolo de acordo com NF P 94-282
O módulo de reação do subsolo kh, de acordo com NF P94-282:2009-03, depende da rigidez na flexão da estrutura de contenção Estr Istr e do módulo pressiométrico (Menard) EM. O módulo de reação do subsolo é dado pela formula seguinte:
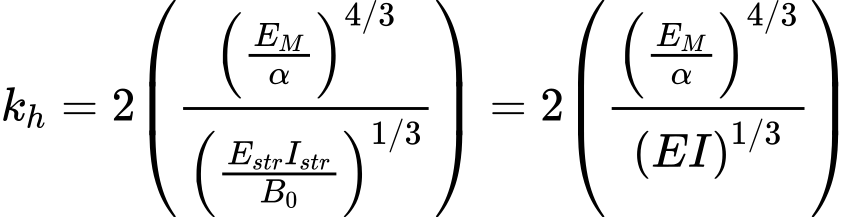
![]()

Valores aproximados para o coeficiente empírico α [–] para vários tipos de solo
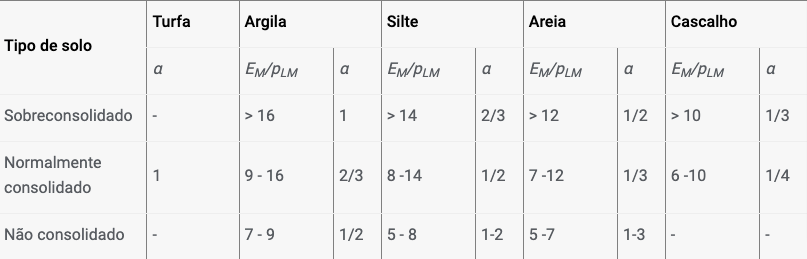
Valores aproximados para o coeficiente empírico α [–] para vários tipos de rocha (de acordo com o grau de degradação)
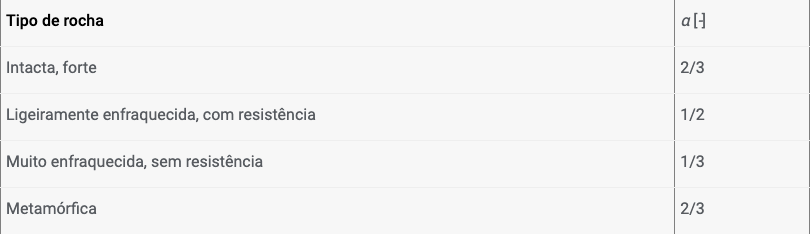
Bibliografia:
NF P94-282: March 2009, pp. 142 – 146.
Módulo de Reação do Subsolo especificado pelo Ensaio Dilatométrico (DMT)
O módulo de reação do subsolo kh [MN/m3] é determinado pela fórmula seguinte:
![]()

O valores do coeficiente B dependem da profundidade da escavação H [m], do módulo constrangido MDMT [MPa] e do espaçamento entre contraventamentos.
Bibliografia:
Monaco, P. and Marchetti, S..: Evaluation of the coefficient of subgrade reaction for design of multi-propped diaphragm walls from DMT moduli. Millpress, Rotterdam, 2004, pp. 993 – 1002, ISBN 90 5966 009 9.
Módulo de Reação do Subsolo de acordo com as Normas Chinesas
O cálculo do módulo de reação do subsolo, de acordo com as Normas Chinesas, baseia-se no método “m” da Norma JGJ 120-2012 (Especificação Técnica para Retenção e Proteção de Escavações para Fundações de Edifícios).
Segundo o método “m”, o módulo de reação do subsolo kh é dado pela fórmula seguinte:
![]()

A partir da fórmula anterior, é possível observar que o cálculo do módulo kh é linear em relação à profundidade do ponto em análise.
O coeficiente proporcional m deve ser determinado a partir do ensaio de carregamento horizontal da estaca. Se não existiram resultados de um ensaio, a Norma Chinesa JGJ 120-2012 sugere uma fórmula empírica para estimar este coeficiente:
![]()

Os outros métodos (método “c” e método “k”) não estão publicados na Norma JGJ 120-2012, mas baseiam-se na experiência e são usados correntemente na China. O módulo de reação do subsolo kh é dado pela fórmula seguinte:
![]()
Se o expoente n = 0,5, é o método “c” e a = c (kN/m3.5).
Se o expoente n = 0, é o método “k” e a = K (kN/m3).
Para o método “m“, n = 1.
Bibliografia:
JGJ 120-2012 (Technical specification for retaining and protection of building foundation excavations).
Módulo de Reação do Subsolo Não Linear
O modelo não linear descreve a dependência do módulo de reação do subsolo kh – isto é, a alteração de kh entre os valores limite correspondentes à rotura devido ao empuxo de terra passivo Tp e ao empuxo de terra ativo Ta – ver figura (o módulo de reação do subsolo é dado pela inclinação da curva; para a pressão nos poros atuante na estrutura é possível considerar o valor de kh1). Este modelo também considera molas como apoios e deformações forçadas da estrutura, várias condições de fronteira, aplicação de suportes e ancoragens, etc.
Os valores para o módulo de reação do subsolo podem ser derivados a partir de valores de módulos de reação do subsolo secantes (CUR 166) – ver figura:
Muro tipo Berlim (Contenção Suportada)
Ao analisar contenções suportadas (cortina de estacas, secções metálicas tipo I ou secções personalizadas), é adotado o seguinte método para determinar os empuxos de terra:
Até à profundidade da vala, os empuxos são determinados para 1 rm da largura da estrutura. Abaixo do fundo da vala, os empuxos de terra são multiplicados pelo coeficiente de redução k (o “Coeficiente de redução de pressão abaixo do fundo da vala“). Este coeficiente pode ser introduzido (na janela “Geometria”, com um parâmetro da secção da estrutura) ou calculado automaticamente.
Se um “Aterro de solo” (janela “Escavação”) for inserido, os empuxos para esta secção são computados para toda a largura da parede (k = 1).
O Coeficiente de redução de pressão abaixo do fundo da vala k pode ser determinado, de forma aproximada (para um dimensionamento muito conservativo), através de:
![]()

Os valores para o módulo de reação do subsolo podem ser derivados a partir de valores de módulos de reação do subsolo secantes (CUR 166) – ver figura:
Aduelas
As aduelas são consideradas como vigas simplesmente apoiadas. O comprimento da viga l é igual ao espaçamento das estacas tipo soldado.
Os valores máximos das forças internas (momento fletor e esforço transverso) são calculados de acordo com o tipo de carregamento selecionado:
![]() Retângulo:
Retângulo:
![]()
![]()
![]() Triângulo:
Triângulo:
![]()
![]()

Escoras
O programa calcula automaticamente as forças internas de acordo com o esquema selecionado na janela “Escoras”. A viga pode ser solicitada por uma carga concentrada R ou carga uniforme q. O valor da carga uniforme q é calculado de acordo com:![]()
| Onde: | n | – | número de apoios |
| Fmax | – | força máxima na ancoragem (suporte) | |
| l | – | ancoragem ou suporte | |
| lo | – | comprimento das saliências (l/2) |
Para as escoras que não estão definidas com o mesmo ângulo que as ancoragens ou suporte, o valor da carga é reduzido por cos(α). As escoras podem ser dimensionadas de acordo com os seguintes esquemas:
No caso de uma viga simplesmente apoiada – carga concentrada, a ancoragem (suporte) é considerada como uma carga concentrada a meio vão da viga. A viga é suportada pelos perfis do muro. Nos restantes casos, as ancoragens e apoios são considerados como apoios da viga. Nota: As escoras são verificadas apenas no plano perpendicular à estrutura do muro, na direção das ancoragens.
Parede de Estacas de Fieira Dupla
O programa permite modelar uma parede de estacas de fieira dupla na janela “Geometria”. A estrutura consiste em três partes: Modelo de cálculo – 1) fieira da frente, 2) fieira de trás, 3) viga de ligação
Modelo de cálculo – 1) fieira da frente, 2) fieira de trás, 3) viga de ligação
A estrutura é solicitada por três cargas principais:
![]()
| Onde: | pc | – | pressão resultante |
| kc | – | coeficiente de rigidez do solo entre as fieiras de trás e da frente | |
| Δv | – | variação da deformação entre as fieiras de trás e da frente | |
| pc,0 | – | empuxo de terra inicial atuante entre as fieiras de trás e da frente |
O coeficiente de rigidez do solo é calculado da seguinte forma:
![]()
| Onde: | Eoed | – | módulo edométrico |
| sy | – | espaçamento entre a fieira de trás e da frente | |
| d | – | diâmetro ou altura da secção transversal |
O empuxo de terra inicial entre as fieiras de trás e da frente é determinado da seguinte forma:
![]()
![]()
| Onde: | α | – | coeficiente de cálculo; se α > 1 então α = 1 |
| pa | – | empuxo de terra ativo | |
| sy | – | espaçamento entre a fieira de trás e da frente | |
| d | – | diâmetro ou altura da secção transversal | |
| h | – | profundidade final da escavação | |
| φm | – | valor médio do ângulo de atrito interno |
Fortalecimento do Solo
O programa pode modelar o fortalecimento do solo na base da estrutura de contenção. O fortalecimento do solo é executado após a instalação de estacas ou paredes fixas por argamassa à base. Os parâmetros decisivos são a altura do solo fortalecido hs ou a largura do solo fortalecido ws e os parâmetros do solo fortalecido (φ, c). O princípio desta solução é demonstrado na figura seguinte.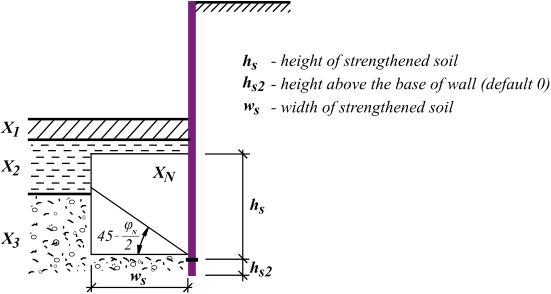 Fortalecimento do solo na base da estrutura de contenção – apresentação gráfica do princípio da solução
Fortalecimento do solo na base da estrutura de contenção – apresentação gráfica do princípio da solução
O princípio para o cálculo do fortalecimento do solo na base da estrutura de contenção é o seguinte:
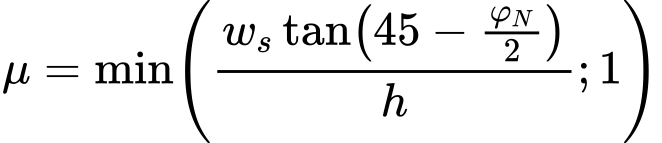
![]()
| onde: | N | – | nova camada de solo fortalecido |
| μ | – | rácio (parâmetro auxiliar) | |
| Xi | – | parâmetro arbitrário na iésima camada do solo | |
| Xoi | – | parâmetro original na iésima camada do solo | |
| XN | – | novo parâmetro de solo fortalecido | |
| ws | – | largura do solo fortalecido [m] | |
| hs | – | altura do solo fortalecido [m] |
Estabilidade Interna das Ancoragens
A estabilidade interna do sistema de ancoragens em contenções é determinado para cada camada de forma independente. A análise de verificação determina uma força de ancoragem, que equilibra o sistema de forças atuantes num bloco de solo. O bloco é contornado pela contenção, terreno, linha que une a base da estrutura com a raiz da ancoragem e por uma linha vertical que atravessa o centro da raiz da ancoragem e do terreno. A fundação teórica da estrutura de contenção é o ponto em que o somatório de forças horizontais atuantes sob a base do poço de construção é igual a zero. Se este ponto estiver abaixo da fundação do muro de contenção, o ponto teórico é a fundação deste muro. A análise é realizada para um metro de desenvolvimento da estrutura de contenção. As forças de ancoragem são computadas de acordo com o seu espaçamento entre camadas.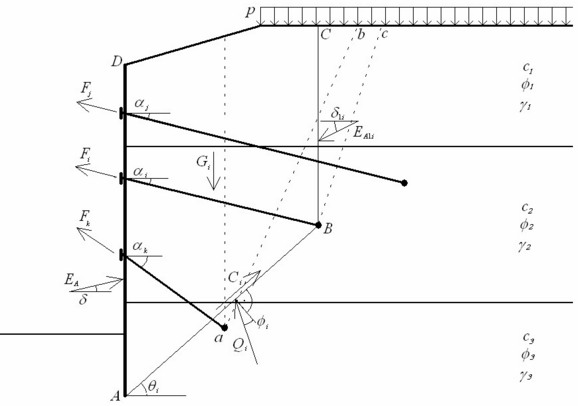 Análise da estabilidade interna
Análise da estabilidade interna
A figura mostra o esquema para a verificação da iésima camada de ancoragens. A força de equilíbrio para o bloco ABCD está a ser determinada. As forças seguintes entram na análise:
| EA | – | resultante do empuxo de terra ativo atuante na contenção (linha AD) |
| EAi | – | resultante do empuxo de terra ativo acima da raiz da ancoragem verificada (linha BC) |
| Gi | – | peso do iésimo bloco de solo ABCD; este valor incorpora a sobrecarga p, aplicada na superfície do terreno, com a inclinação θi da superfície de deslizamento AB a ser superior que o valor médio do ângulo de atrito interno nesta superfície; caso a inclinação da superfície de deslizamento AB seja inferior, a sobrecarga no terreno não é considerada |
| Ci | – | resultante da coesão do solo na superfície de deslizamento AB |
| Fj, Fk,… | – | forças desenvolvidas em outras ancoragens, mas que são consideradas; apenas as ancoragens “mais curtas” (comparativamente com a iésima ancoragem) contribuem para a análise de equilíbrio do iésimo bloco; o seguinte princípio é utilizado para decidir se um dada ancoragem (a mésima) é incluída ou excluída do equilíbrio do iésimo bloco: primeiro, a ancoragem inferior é selecionada (a mésima ou a iésima); seguidamente, uma superfície de deslizamento plane é inserida a partir do centro da raiz da ancoragem selecionada; este plano tem uma inclinação de 45o – φn/2 a partir da vertical (linha ab ou Bc, na figura); φn é o valor médio do ângulo de atrito interno acima da raiz da ancoragem inferior: se a iésima raiz estiver acima da méso,a e a localização mais elevada da raiz (a iésima) estiver fora da área atravessada pela superfície de deslizamento plana, então a mésima ancoragem não é incluída na análise; o mesmo exemplo é válido para incluir a mésima ancoragem quando a iésima raiz está sob a mésima e esta mésima raiz está localizada dentro da área atravessada pela superfície de deslizamento; os dois casos opostos excluem as ancoragens da análise; primeiro, o da iésima raiz acima da mésima e a iésima dentro da área, o segundo é quando a iésima raiz está abaixo da mésima e a mésima está fora da área; conforme a definição anterior, a ancoragem “mais curta” Fk é incluída na análise e a ancoragem “mail longa” Fj é excluída da análise (ver figura) |
| Qi | – | reação na superfície de deslizamento AB |
| Fi | força na ancoragem analisada, o valor máximo permitido para esta força é o resultado da análise de equilíbrio realizada para o iésimo bloco |
A solução do equilíbrio para um dado bloco implica definir as equações de equilíbrio para as forças verticais e horizontais. Estas representam um sistema de duas equações, tendo como incógnitas a reação do subsolo Qi e valor máximo permitido para a força de ancoragem Fi. Como resultado, o programa obtém o valor máximo permitido para a força de ancoragem, para cada fieira de ancoragens. Estes valores são comparados com os definidos previamente para as ancoragens.
Verificação do Fundo da Vala
A verificação standard para heave e piping é realizada apenas para o caso da pressão hidrodinâmica quando o calço da estrutura está submerso em um solo permeável, que permite o escoamento de água livre abaixo da estrutura. Esta verificação está de acordo com a Norma EN1997-1.
A verificação do fundo da vala de acordo com as Normas Chinesas (ex.: upheavel de acordo com a superfície de deslizamento de Prandtl ou o efeito do aquífero confinado) está disponível para todos os tipos de Nível Freático. Estas verificações não costumam ser impostas e apenas estão disponíveis para análises de acordo com as Normas Chinesas.
Failure by Heave and Piping (EN1997-1)
Rotura devido a heave
A estabilidade do solo contra heave devido à percolação de água no subsolo (HYD) é verificada de acordo com os estados limite, pela equação:![]()
| onde: | udst | – | pressão hidrostática desvaforável |
| σstb | – | peso do solo favorável | |
| γh | – | coeficiente de redução para a rotura devido a heave |
![]()
| onde: | udst | – | pressão hidrostática desvaforável |
| σstb | – | peso do solo favorável | |
| SFh | – | fator de segurança para a rotura devido a heave |
 Rotura por heave – esquema da estrutura de contenção
Rotura por heave – esquema da estrutura de contenção
Rotura devido a piping
A rotura devido a piping é verificada de acordo com os estados limite pela equação:![]()
| onde: | i | – | gradiente hidráulico |
| ic | – | gradiente hidráulico crítico, para o qual ic = γsu/γw | |
| γp | – | coeficiente de redução da erosão interna so solo |
![]()
| onde: | i | – | gradiente hidráulico |
| ic | – | gradiente hidráulico crítico, para o qual ic = γsu/γw | |
| SFp | – | fator de segurança para a erosão interna do solo |
Verification of Ditch Bottom according to Chinese Standards
The program allows us to perform three independent verifications of ditch bottom according to Chinese standards:
![]() Upheavel check
Upheavel check
![]() Heave check
Heave check
![]() Piping of soil
Piping of soil
Upheavel Check according to Chinese Standard
This verification follows the Prandtl analysis of foundation soil bearing capacity.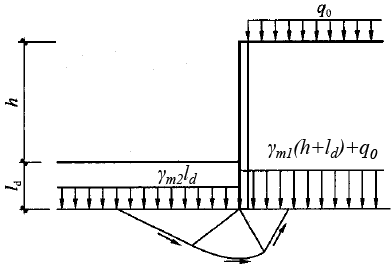 Upheavel check scheme – Prandtl slip surface
Upheavel check scheme – Prandtl slip surface
![]()
![]()
![]()
| where: | SFu | – | safety factor of upheaval |
| γm1 | – | weighted average value of the soil unit weight behind the structure | |
| γm2 | – | weighted average value of the soil unit weight in front of the structure | |
| ld | – | embedded depth of the structure | |
| h | – | depth of the foundation pit | |
| q0 | – | uniform load on the terrain | |
| Nc, Nq | – | coefficients of bearing capacity | |
| c, φ | – | cohesion and internal friction angle of soil below the bottom of structure |
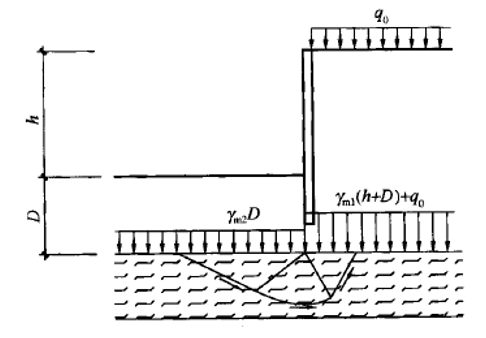 Principle of the verifciation in case of a layer in a depth D
Principle of the verifciation in case of a layer in a depth D
Heave Check according to Chinese Standard
This verification depends on the depth of confined aquifer D and height of its confined water level hw to which the water would rise if it was not restricted by aquifuge from above.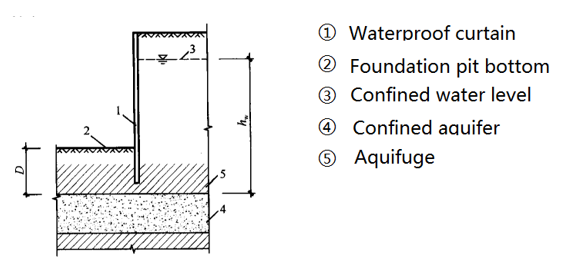
![]()
| where: | SFh | – | safety factor of stability of the soil against heave |
| D | – | Distance between the top of the confined aquifer and the bottom of foundation pit | |
| γ | – | Unit weight of the soil layer between the top of confined aquifer and the bottom of foundation pit | |
| hw | – | Pressure head from the top of confined aquifer | |
| γw | – | Unit weight of water |
Piping Check according to Chinese Standard
This verification can be used for both phreatic and confined water levels.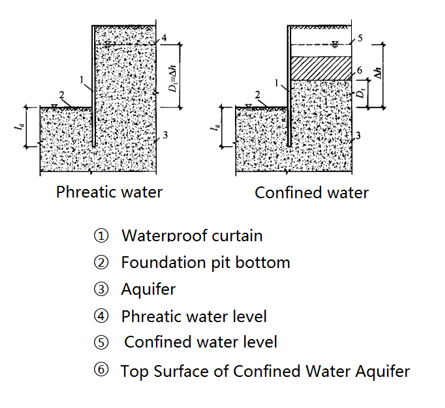
Verification is done using safety factor approach and follows formulas:
![]()
| where: | SFp | – | Safety factor of stability of the soil against piping |
| ld | – | Length of the waterproof curtain below the bottom of the pit | |
| D1 | – | Depth between the bottom of foundation pit and phreatic water level or top surface of the confined water aquifer | |
| γ´ | – | Unit weight of soil under the buoyant force | |
| Δh | – | Difference of waterhead between the inside and outside of the foundation pit | |
| γw | – | Unit weight of water |
Assentamento do Terreno atrás da Estrutura de Escoramento
O assentamento do terreno atrás da estrutura de escoramento pode ser analisado de acordo com as teorias seguintes:
![]() Método do triângulo
Método do triângulo
![]() Método do índice
Método do índice
![]() Método da parábola
Método da parábola
![]() DG/TJ08-61-2010
DG/TJ08-61-2010
Método do Triângulo
Segundo o Método do triângulo, o assentamento do terreno atrás da estrutura de escoramento é calculado através da fórmula seguinte: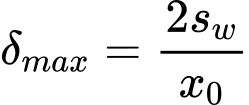
| onde: | δmax | – | assentamento máximo |
| sw | – | área compreendida entre a estrutura deformada e a estrutura indeformada | |
| x0 | – | largura do assentamento |
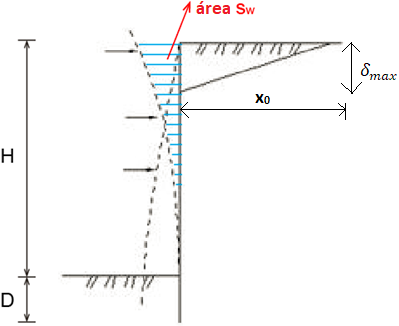
A largura do assentamento do terreno x0 é dada por:
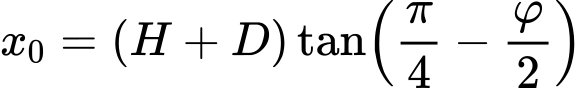
| onde: | H | – | profundidade da escavação |
| D | – | comprimento da estrutura abaixo da base do poço de fundação | |
| φ | – | média ponderada do ângulo de atrito interno de todas as camadas de solo que a estrutura atravessa |
Método do Índice
Segundo o Método do índice, o assentamento do terreno atrás da estrutura de escoramento é calculado através da fórmula seguinte: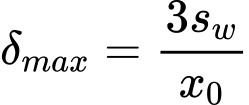
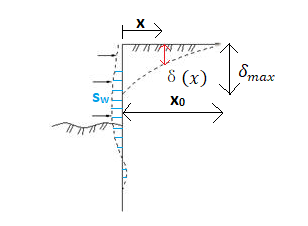
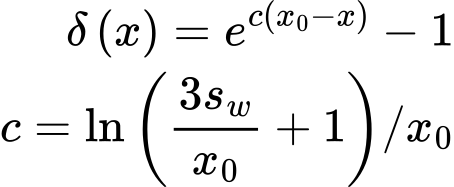
| onde: | δmax | – | assentamento máximo |
| sw | – | área compreendida entre a estrutura deformada e a estrutura indeformada | |
| x0 | – | largura do assentamento | |
| δ(x) | – | assentamento em cada ponto compreendido na largura do assentamento x0 para cada distância x | |
| x | – | distância entre o ponto calculado e a extremidade do poço de fundação |
Método da Parábola
Segundo o Método da parábola, o assentamento do terreno atrás da estrutura de escoramento é calculado através da fórmula seguinte:![]()
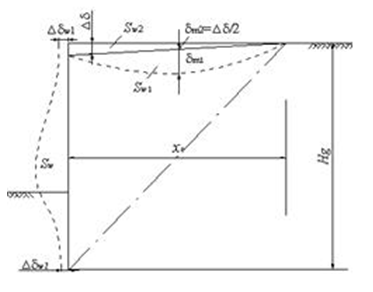
![]()
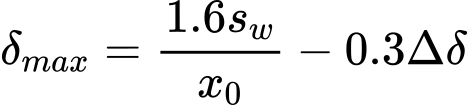
| onde: | δmax | – | assentamento máximo |
| sw | – | área compreendida entre a estrutura deformada e a estrutura indeformada | |
| x0 | – | largura do assentamento | |
| δ(x) | – | assentamento em cada ponto compreendido na largura do assentamento x0 para cada distância x | |
| x | – | distância entre o ponto calculado e a extremidade do poço de fundação | |
| δw1 | – | deslocamento horizontal no topo da estrutura | |
| δw2 | – | deslocamento horizontal na base da estrutura |
DG/TJ08-61-2010
Settlement of terrain behind the shoring structure is calculated according to the DG/TJ08-61-2010 (Technical code for excavation engineering in Shanghai) and it is suitable for using in soft soils. Settlement behind the sheeting differs in two parts – main influence area and secondary influenced area.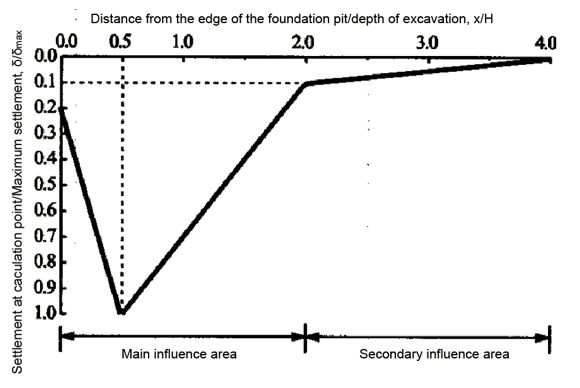
![]()
| where: | δmax | – | maximum settlement |
| δhm | – | maximum horizontal displacement of structure |
The range of settlement x0 is calculated as follows:
![]()
| where: | x0 | – | range of settlement |
| H | – | depth of excavation |
Settlement at each point δ(x) in range of settlement x0 is calculated as follows:
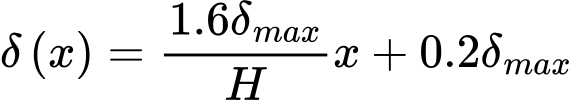
| where: | δ(x) | – | Settlement at each point within the range of settlement or influenced area |
| x | – | Distance between the calculation point and the edge of the foundation pit |
Literature: DG/TJ08-61-2010 (Technical code for excavation engineering in Shanghai)
Utilização da Resistência Passiva
O programa permite comparar a resistência passiva máxima permitida com a efetiva sob do fundo da vala. Caso as Normas não obriguem a esta verificação, esta pode ser utilizada para a otimização do comprimento da estrutura embutido no solo. A verificação é realizada através do método do fator de segurança:![]()
| onde: | SFp | – | Fator de segurança imposto para a utilização da resistência passiva |
| Rmax | – | Resistência passiva máxima permitida sob o fundo da vala | |
| Rmob | – | Resistência passiva mobilizada sob o fundo da vala |
Rmob fica realçada através de um padrão.
Utilização da resistência passiva
Capacidade de Suporte Vertical
O programa permite as seguintes análises:
![]() mobilização da resistência do solo
mobilização da resistência do solo
![]() capacidade de suporte vertical
capacidade de suporte vertical
Ambas as análises podem ser verificadas de acordo com os fatores de segurança (ASD) ou com a Norma Alemã EB9/EB84.
Mobilização da Resistência do Solo
Mobilização da resistência do soloForças atuantes na estrutura
Verificação de acordo com a metodologia dos Fatores de Segurança (ASD):![]()
![]()
![]()
![]()
| onde: | SFf | – | fatores de segurança necessários para a mobilização da resistência do solo |
| Pv | – | carga vertical permanente | |
| Av | – | forças verticais devidas às ancoragens | |
| G | – | peso próprio do muro | |
| Eav | – | força de atrito atrás do muro | |
| Bv | – | força de atrito à frente do muro |
Capacidade de Carga Vertical
Capacidade de carga verticalForças atuantes na estrutura
Verificação de acordo com a metodologia dos Fatores de Segurança (ASD):![]()
![]()
![]()
![]()
| onde: | SFv | – | fator de segurança necessário para a capacidade de carga vertical |
| V | – | força vertical (permanente e transitória) | |
| Pv | – | força vertical permanente | |
| Pv,t | – | força vertical transitória | |
| γG | – | fator parcial para a força permanente | |
| γQ | – | fator parcial para a força transitória | |
| Av | – | forças verticais devido às ancoragens | |
| G | – | peso próprio do muro | |
| Eav | – | força de atrito atrás do muro | |
| Bv | – | força de atrito à frente do muro | |
| Rb | – | resistência da base | |
| Rs | – | resistência da vala | |
| kV | – | fator de redução da capacidade de carga vertical |
Resistência da Base
A capacidade de carga vertical é dada pela fórmula seguinte:![]()
| onde: | Rb | – | resistência da base |
| Ab | – | área da base | |
| q0 | – | resistência de pico da base |
A determinação da resistência de pico qo deve ser de acordo com a prospeção geológica. Os valores recomendados para a resistência de pico qo [MPa] podem ser encontrados em bibliografia técnica para solos e tipos de estruturas específicos: – para estacas-prancha
| solo não coesivo | |||
| qc | 7,5 | 15 | 25 |
| q0 | 7,5 | 15 | 20 |
– para estacas cravadas
| q0 | ||||||
| solo não coesivo | solo coesivo | |||||
| qc | cu | |||||
| s/Deq | 7,5 | 15 | 25 | 100 | 150 | 200 |
| 0,035 | 2,200-5,000 | 4,000-6,500 | 4,500-7,500 | 0,350-0,450 | 0,55-0,700 | 0,80-0,950 |
| 0,100 | 4,200-6,000 | 7,600-10,200 | 8,7500-11,500 | 0,600-0,750 | 0,85-0,110 | 0,115-0,150 |
– para estacas escavadas
| q0 | ||||||
| solo não coesivo | solo coesivo | |||||
| qc | cu | |||||
| s/Deq | 7,5 | 15 | 25 | 100 | 150 | 250 |
| 0,02 | 0,550-0,800 | 1,050-1,400 | 1,750-2,300 | 0,350-0,450 | 0,600-0,750 | 0,950-1,200 |
| 0,03 | 0,700-1,050 | 1,350-1,800 | 2,250-2,950 | 0,450-0,550 | 0,700-0,900 | 1,200-1,450 |
| 0,10 | 1,600-2,300 | 3,000-4,000 | 4,000-5,300 | 0,800-1,000 | 0,1200-0,1500 | 1,600-2,000 |
| onde: | qc | – | resistência de penetração de cone, CPT [MPa] |
| cu | – | coesão total do solo [kPa] | |
| s | – | assentamento da estaca | |
| Deq | – | diâmetro da estaca |
Capacidade de Carga da Vala
A capacidade de carga vertical é dada pela fórmula seguinte:![]()
| onde: | Rs | – | resistência da vala |
| As | – | área de contacto | |
| qs | – | atrito superficial |
A determinação do atrito superficial qs deve ser de acordo com a prospeção geológica. Os valores recomendados para atrito superficial qs [kPa] podem ser encontrados em bibliografia técnica para solos e tipos de estruturas específicos: – para estacas-prancha
| solo não coesivo | |||
| qc | 7,5 | 15 | 25 |
| qs | 20 | 40 | 50 |
– para estacas cravadas
| qs | ||||||
| solo não coesivo | solo coesivo | |||||
| qc | cu | |||||
| s/Deq | 7,5 | 15 | 25 | 100 | 150 | 200 |
| ssg* | 30-40 | 65-90 | 85-120 | 20-30 | 35-50 | 45-65 |
| ssg=sg=0,1Deq | 40-60 | 95-125 | 125-160 | 20-35 | 40-60 | 55-80 |
– para estacas escavadas
| solo não coesivo | |||
| qc | 7,5 | 15 | 25 |
| qs | 55-80 | 105-140 | 130-170 |
| onde: | qc | – | resistência de penetração de cone, CPT [MPa] |
| cu | – | coesão total do solo [kPa] | |
| ssg* | – | assentamento que leva à ativação da resistência da vala | |
| ssg=sg | – | assentamento limite |
Estaca Anti-deslizante
O programa Estaca Anti-deslizante executa a análise de estacas anti-deslizantes (cálculo das forças internas + deslocamentos, dimensionamento da secção transversal da estaca). A análise da estrutura é semelhante ao do programa Verificação de Contenções, diferindo na determinação de pressões acima da superfície de deslizamento e na possibilidade de modelar a estaca encastrada num maciço rochoso.
Caso se verifique que um talude, ou estrutura, tenham sido introduzidos sob uma superfície de deslizamento que não esteja aceitável, é possível aumentar a estabilidade do talude ao inserir uma estaca anti-deslizante (a janela “Estacas anti-deslizantes” serve para realizar este passo no programa “Estabilidade de Taludes”). A estaca deve ser introduzida de forma a atravessar a superfície de deslizamento, com sua base a atingir profundidades bastante superiores às da superfície de deslizamento. Acima da superfície de deslizamento, a estaca é carregada por uma força ativa T, com tendência para mover a estaca, e por uma força passiva (resistente) P, que estabiliza a estaca (ver figura). A diferença entre as forças passiva e ativa cria uma carga que deve ser transferida pela estaca de modo a aumentar a estabilidade da superfície de deslizamento, cumprindo o valor de FSs.
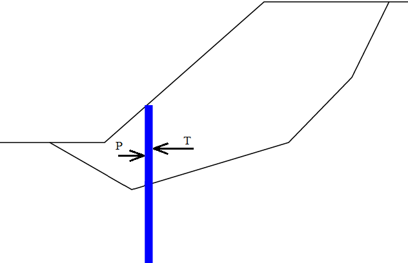 Esquema das forças ativa e passiva atuantes numa estaca anti-deslizante
Esquema das forças ativa e passiva atuantes numa estaca anti-deslizante
Se o FS para a estabilidade do talude sem uma estaca anti-deslizante for suficiente, as forças ativa e passiva estão em equilíbrio – a estaca não está carregada e não há necessidade de recorrer a uma estaca anti-deslizante. Para o cálculo das forças atuantes na estaca, é importante que o fator de segurança FSs imposto seja superior ao FS calculado para a superfície de deslizamento sem a estaca, ou que o fator de segurança importo seja superior ao associado à superfície de deslizamento definida para a situação sem estaca anti-deslizante.
Determinação das Forças Atuantes numa Estaca Anti-deslizante
As forças atuantes numa estaca anti-deslizante são calculadas pela análise de estabilidade de taludes. O cálculo do FS para a estabilidade do talude baseia-se na análise de equilíbrio das forças atuantes em blocos de solo acima da superfície de deslizamento. As superfícies verticais de cada bloco estão sujeitas à ação de forças inter-blocos Fi e a sua determinação é um dos passos da análise de estabilidade de taludes. Se os blocos de solo estiverem no mesmo estado limite de equilíbrio, as forças inter-blocos, no início e no fim da superfície de deslizamento, são nulas. O fator de segurança limite FSlim, para o qual o estado limite de equilíbrio é alcançado, é considerado como o fator de segurança real para a superfície de deslizamento definida. A distribuição de forças inter-blocos ao longo do comprimento deslizante é denominado de linha de pressão. As forças atuantes numa estaca anti-deslizante são determinadas a partir da distribuição de linhas de pressão calculadas para o fator de segurança pretendido FSs.
A figura seguinte mostra distribuições diferentes de forças inter-blocos Fi (linhas de pressão). a) mostra a distribuição de forças Fi no estado limite de equilíbrio, quando as forças inter-blocos nulas estão no início e no final da distribuição. Isto significa que este estado foi alcançado para o valor do fator de segurança FSlim, que expressa o grau de segurança da superfície de deslizamento definida. b) mostra a linha de pressão determinada para um fator de segurança superior ao FSlim. Assume-se que a força Fn é nula no topo da superfície de deslizamento e que a força F0,b assume um valor diferente de zero na parte inferior da superfície de deslizamento. Isto significa que para obter o fator de segurança FS, a base do talude deve ser carracaga por uma força de pressão com o valor de F0,b. c) mostra a linha de pressão para um fator de segurança FS superior ao FSlim. Isto resulta da suposição de uma força F0 nula no topo da parte inferior da superfície de deslizamento, sendo encontrada uma força sem compensação Fn,c. Para conseguir o estado de equilíbrio para o fator de segurança FS, seria necessária, teoricamente, a ação de uma força de tração, de igual valor, na parte superior da superfície de deslizamento. d) mostra a distribuição de forças inter-blocos para o caso de uma estaca anti-deslizante ser colocado no ponto x. A parte acima da distribuição corresponde a c) e serve para determinar o valor da força passiva P no ponto x. Acima da estaca, é considerada uma distribuição igual a b) para determinar a força ativa T no ponto x. A diferença entre P e T é a força transmitida pela estaca anti-deslizante.
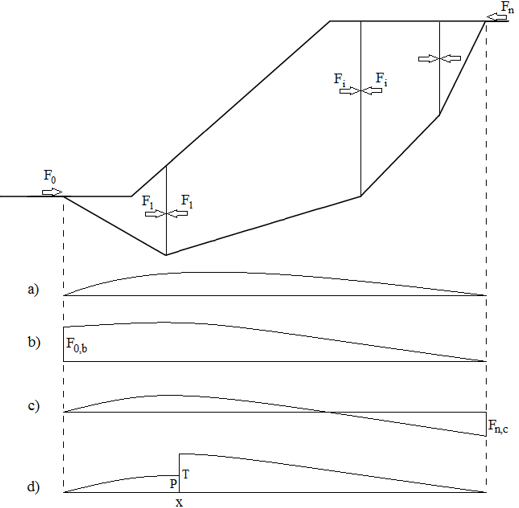 Distribuição de forças inter-blocos Fi
Distribuição de forças inter-blocos Fi
Legenda (explicação):
a) distribuição para o fator de segurança FS = FSlim (F0 = 0 e Fn = 0)
b) distribuição para o fator de segurança FS > FSlim com valor nulo para a força na parte superior
c) distribuição para o fator de segurança FS > FSlim com valor nulo para a força na parte inferior
d) distribuição para o fator de segurança FS com uma estaca anti-deslizante no ponto x
Destribuição de Pressões acima da Superfície de Deslizamento
A distribuição da carga aplicada a uma estaca anti-deslizanta acima da superfície de deslizamento é determinada a partir do valor das forças P e T. São consideradas distribuições constantes, triangulares ou trapezoidais (para o programa “Estaca Anti-Deslizante” a distribuição de forças ativas e passivas é introduzida na janela “Determinação de pressão”). Para a força passiva (resistente) P também pode ser considerada uma distribuição parabólica, que consiste numa aproximação simplificada da combinação de distribuições triangulares e trapezoidais.
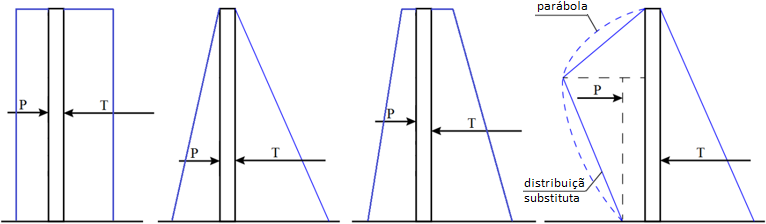 Tipos de distribuições de cargas aplicadas a uma estaca anti-deslizante acima da superfície de deslizamento
Tipos de distribuições de cargas aplicadas a uma estaca anti-deslizante acima da superfície de deslizamento
Recomendações para distribuições de forças ativas
![]() Distribuição triangular – as camadas acima da superfície de deslizamento são de cascalho ou areia
Distribuição triangular – as camadas acima da superfície de deslizamento são de cascalho ou areia
![]() Distribuição retangular – as camadas acima da superfície de deslizamento são de solos granulados finos (argila, silte)
Distribuição retangular – as camadas acima da superfície de deslizamento são de solos granulados finos (argila, silte)
![]() Distribuição trapezoidal – as camadas acima da superfície de deslizamento são de diferentes tipos de solos
Distribuição trapezoidal – as camadas acima da superfície de deslizamento são de diferentes tipos de solos
Cálculo da Força Passiva na Etapa Seguinte
Caso exista uma nova escavação à frente da estaca, a força passiva pode ser calculada automaticamente, de acordo com a fórmula: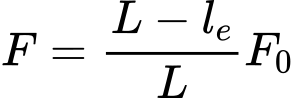
| Onde: | F | – | nova força passiva, após a escavação |
| L | – | profundidade da superfície de deslizamento abaixo do solo, na primeira etapa | |
| le | – | distância entre a superfície do terreno na primeira etapa e na etapa atual | |
| Fo | – | força passiva original, antes da escavação |
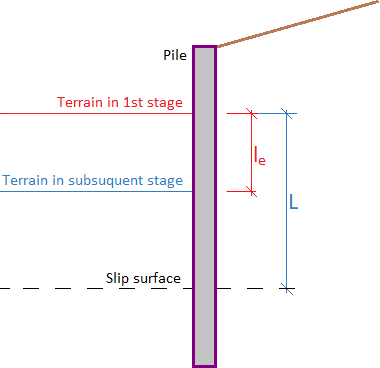
Poço
Na janela “Análise”, o programa poço define as cargas atuantes no poço.
A carga calculada é introduzida na análise de forças internas, na janela “Dimensionamento”.
Cálculo das Cargas Atuantes num Poço
A carga devido ao empuxo de terra e sobrecarga são computadas na janela “Análise”. A rigidez do posso tem uma grande influência no empuxo de terra. Uma estrutura rígida não permite deformações, podendo o empuxo de terra ser muito superior ao verificado num poço flexível.
Podem ser modelados três tipos de poços no programa:
![]() Flexível – é considerada a pressão espacial ativa (empuxo de terra, sobrecarga superficial e sobrecarga local)
Flexível – é considerada a pressão espacial ativa (empuxo de terra, sobrecarga superficial e sobrecarga local)
![]() Semi-rígido
Semi-rígido
![]() Rígido – é considerada a pressão espacial em repouso (empuxo de terra, sobrecarga superficial e sobrecarga local)
Rígido – é considerada a pressão espacial em repouso (empuxo de terra, sobrecarga superficial e sobrecarga local)
Método de determinação de cargas
A carga devido ao empuxo de terra e sobrecarga superficial atuam como cargas uniformes em todo o diâmetro do poço. Estas cargas provocam tensões apenas devido à força normal – o momento fletor no poço é, teoricamente, igual a zero. Para modelar o comportamento real do poço, o programa introduz o coeficiente de redução de acordo com as Normas DIN V 4034-1 ou СНиП II-94-80. O valor recomendado para o coeficiente de redução é 25 %.
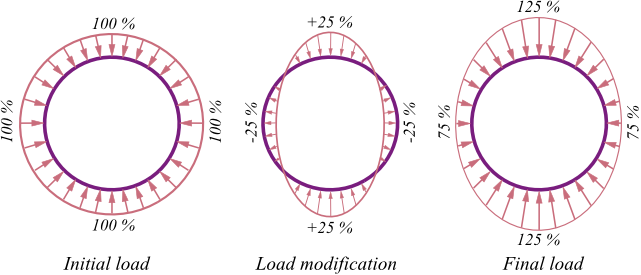 Modificação da carga uniforme pelo coeficiente de redução
Modificação da carga uniforme pelo coeficiente de redução
A carga devido à sobrecarga local é considerada como demonstrado na figura abaixo. Esta carga não é modificada pelo coeficiente de redução.
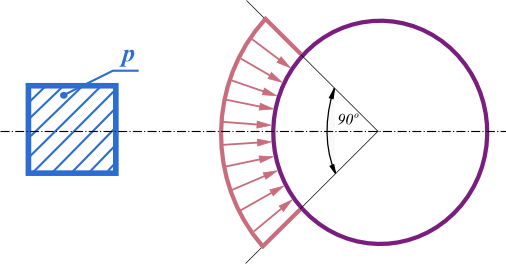 Carga devido à sobrecarga local
Carga devido à sobrecarga local
Cálculo da carga em escoras
Se forem introduzidas escoras, o programa computa a carga atuante em cada uma delas. A carga depende da distância axial entre escoras, conforme mostra a figura.
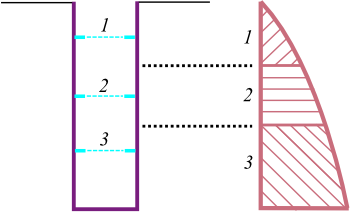 Cálculo da carga em escoras
Cálculo da carga em escoras
Se não forem introduzidas escoras, o programa computa a carga para uma profundidade unitária (1 m, 1 ft).
Ao calcular a carga, o programa determina a distribuição de forças internas na estrutura do poço.
Bibliografia:
Berezantzev, V. G.: Earth pressure on the cylindrical retaining walls, Brussels conference on Earth pressure problems, 1958.
ČSN 73 0037: Zemní tlak na stavební konstrukce, 1990.
DIN 4085: Berechnung des Erddrucks, 1987.
Exner, K.: Hloubení jam, VŠB v Ostravě, 1986.
Cheng, Y. M.; Hu, Y. Y.: Active earth pressure on circular shaft lining obtained by simplified slip line solution with general tangential stress coefficient. Chinese Journal of Geotechnical Engineering, 27 (1), 110-115, 2005.
Link, H.; Lutgendorf, H.; Stoss, K.: Richtlinien zur Berechnung von Schachtauskleidungen in nicht standfestem Gebirge, 1976.
Sedláček, M.: Zatížení kruhových šachet prostorovým zemním tlakem. Příspěvek ke konferenci Zakládání staveb, 2014.
Snášelová, K.: Hloubení a vyztužování jam v extrémních podmínkách, ODIS VTEI pro uhelný průmysl, 1987.
Tobar, T.; Meguid, M.: Distribution of active earth pressure on vertical shafts, Geo Halifax, 2009.
Valencia, T. T.: An experimental study of the earth pressure distribution on cylindrical shafts, McGill University, Montreal, 2009.
Walz, B.; Pulsfort, M.: Raumliche Erddruck auf Schachtbauwerke in Abhangigkeit von der Wandverformung, Bergische Universitat Wuppertal, 1999.
Estruturas de Poços Flexíveis
O método de escavação convencional é um exemplo típico de poços com estruturas flexíveis. Através deste método, a rocha é escavada numa primeira fase e, seguidamente, é projetado concreto para endurecer a superfície, de modo a suportar a rocha. Existem tecnologias específicas (escavação do terreno, concreto projetado, arcos em madeira) que permitem que as tensões sejam redistribuídas ao longo do solo que envolve o poço e, consequentemente, o valor do empuxo de terra atuante no poço será igual ao do empuxo de terra ativo. O método de V.G. Berezantsev’s (1958) descreve esta situação. A carga em poços flexíveis é definida através da seguinte fórmula:![]()
| onde: | γ | – | peso volúmico do solo |
| h | – | profundidade da secção transversal | |
| q | – | valor da sobrecarga | |
| cef | – | força de cisalhamento do solo |
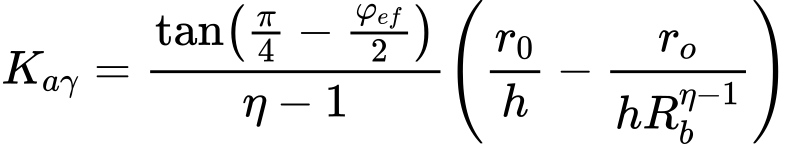
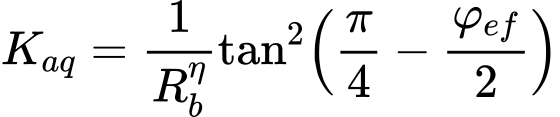
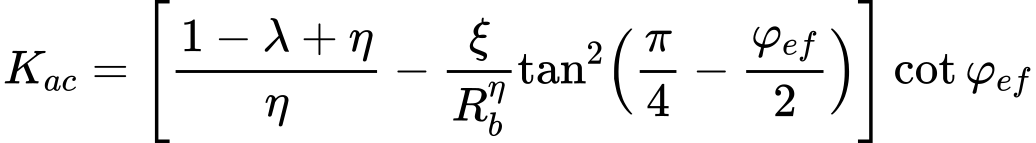
| onde: | r0 | – | raio do poço |
| φef | – | ângulo de atrito interno do solo | |
| ξ = 1 | |||
| λ = 1 |
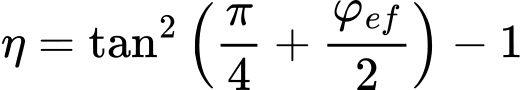
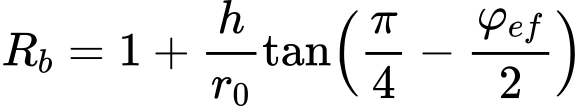
Estruturas de Poços Semi-rígidas
As estacas-prancha são um exemplo típico de suportes semi-rígidos para poços. As estacas-prancha são cravadas no chão durante a primeira etapa de construção, antes da escavação do solo. A redistribuição parcial das tensões do solo em torno do poço é possível devido à leveza da estrutura. O valor resultante para o empuxo de terra atuante na estrutura do poço está compreendido entre o empuxo de terra ativo e em repouso.
A carga num poço semi-rígido é considerada como o valor médio entre a carga em poços flexíveis e a carga em poços rígidos.
Estruturas de Poços Rígidas
As paredes de estacas secantes são um exemplo típico de suportes rígidos para poços. Na primeira etapa de construção, a estrutura do poço é executada e o solo é escavado. A carga atuante no poço devido ao empuxo de terra é igual ao empuxo de terra em repouso, uma vez que as estruturas rígidas têm deformações mínimas. O comportamento destas estruturas é descrito pela teoria de Y. M. e Y. Y. Hu (2005). A carga em poços rígidos é definida através da seguinte fórmula:![]()
| onde: | γ | – | peso volúmico do solo |
| h | – | profundidade da secção transversal | |
| q | – | valor da sobrecarga | |
| cef | – | força de cisalhamento do solo |
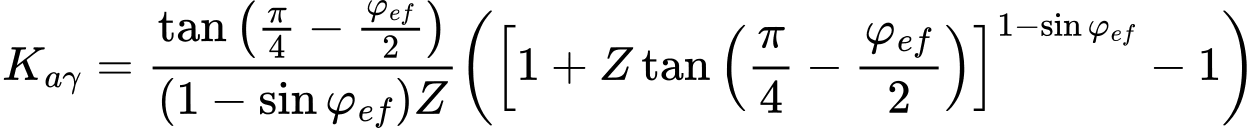
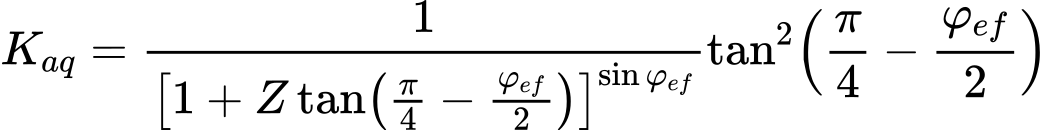
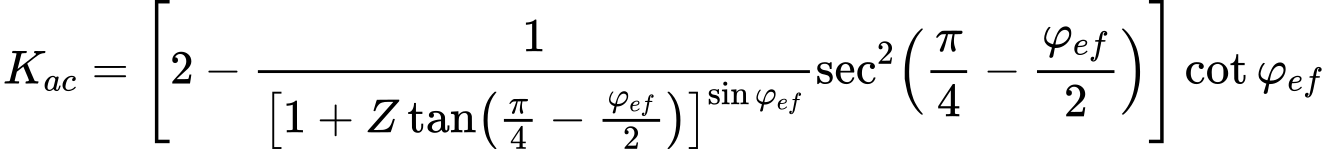
| onde: | r0 | – | raio do poço |
| φef | – | ângulo de atrito interno do solo | |
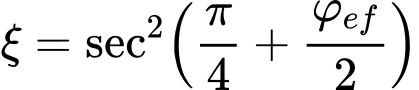
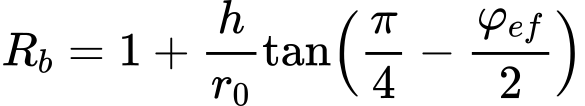
![]()
Cálculo das Forças Internas num Poço (Dimensionamento)
O programa permite analisar as forças internas atuantes na estrutura, nas direções horizontal e vertical, para uma certa carga atuante no poço.
Análise de forças internas na direção vertical
O modelo analítico da estrutura é demonstrado na figura. Todas as escoras são modeladas como suportes. A análise é realizada para uma largura unitária (1 m, 1 ft) da estrutura. As estruturas sem escoras, ou apenas com uma escora, não podem ser analisadas na direção vertical.
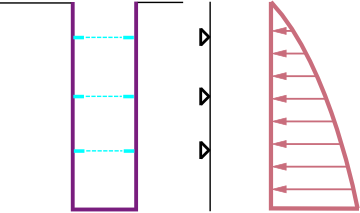 Modelo analítica para a direção vertical
Modelo analítica para a direção vertical
Análise de forças internas na direção horizontal (método poligonal)
As forças internas na direção horizontal são computadas pelo método poligonal, em que a estrutura circular é dividida em 72 segmentos. Cada segmento é suportado por uma mola não linear, atuando apenas à compressão. A rigidez das molas é igual ao módulo de reação do subsolo introduzido.
O método da análise é demonstrado na figura – se a estrutura sofrer deformações na direção do centro, as molas são removidas da análise.
 Modelo analítica para a direção horizontal
Modelo analítica para a direção horizontal
Estabilidade de Taludes
O programa Estabilidade de Taludes calcula a estabilidade de taludes naturais e de aterros com superfícies de deslizamento circulares ou poligonais.
O problema da estabilidade de taludes é resolvido num ambiente de duas dimensões. Pode ocorrer a existência de taludes abaixo do nível freático, com o nível de água a ser superior à cota da base do talude, que pode estar inundado total ou parcialmente. O talude pode ser carregado por uma sobrecarga, com uma qualquer forma, quer na superfície, quer no subsolo. A análise permite incluir o efeito de ancoragens capazes de suportar o talude, incluir elementos horizontais de reforço – reforços, ou incluir elementos verticais – estacas anti-deslizantes. Os efeitos de sismos também podem ser considerados na análise.
Estão implementados dois tipos de aproximação à análise da estabilidade de taludes – análise clássica de acordo com o fator de segurança e a análise de acordo com os estados limite.
A superfície de deslizamento pode ser modelada de duas formas diferentes. Pode ser circular, em que o usuário pode escolher os métodos de Fellenius/Petterson, Bishop, Spencer, Janbu ou Morgenstern-Price, Shahunyants, ITF, ou pode ser poligonal, em que o usuário pode escolher os métodos de Sarma, Spencer, Janbu ou Morgenstern-Price, Shahunyants, ITF.
Solo
O solo é formado por um perfil em camadas. Pode ser utilizado um número arbitrário de camadas. Cada camada é definida pela sua geometria e material. O material de uma camada é representado por solo com propriedades específicas. Durante a análise é determinada a tensão geostática do solo.
As camadas também podem ser definidas como corpos rígidos. Essas camadas podem representar o bedrock ou uma cortina de contenção. A superfície de deslizamento nunca pode atravessar um corpo rígido.
Influência do Nível Freático
Há cinco opções para definir a posição do nível freático:1) Nível Freático
O nível freático pode ser definido como um polígono. Pode ter uma curvatura aleatória, coincidir totalmente com a superfície ou estar parcialmente acima da superfície. A presença de água influencia o valor da pressão nos poros, reduzindo a resistência ao cisalhamento do solo. A pressão nos poros é considerada como uma pressão hidrostática, isto é, o peso volúmico da água é multiplicado pela altura reduzida do nível freático:![]()
| onde: | γw | – | peso volúmico da água |
| hr | – | altura reduzida do nível freático |
![]()
| onde: | h | – | distância vertical entre o ponto onde a pressão é calculada e a cota do lençol freático |
| α | – | inclinação |
![]()
| onde: | u | – | pressão no poro de um certo ponto |
| l | – | comprimento da secção |
![]()
| onde: | T | – | força de cisalhamento na superfície de deslizamento |
| N | – | força normal à superfície de cisalhamento | |
| U | – | pressão nos poros resultante na superfície de cisalhamento | |
| φ | – | ângulo de atrito interno | |
| c | – | coesão do solo | |
| d | – | comprimento da superfície de deslizamento |
2) Nível freático incluindo sucção
Pode ser introduzida uma superfície de sucção acima do nível freático. É assumido um valor negativo para a pressão nos poros u para a zona de fronteira entre as duas regiões. A sucção aumenta como impulsão hidrostática negativa do nível freático, na direção da superfície de sucção.3) Rebaixamento rápido
O nível freático original pode ser introduzido acima do nível freático desejado. O nível freático original representa o estado antes de um rebaixamento rápido.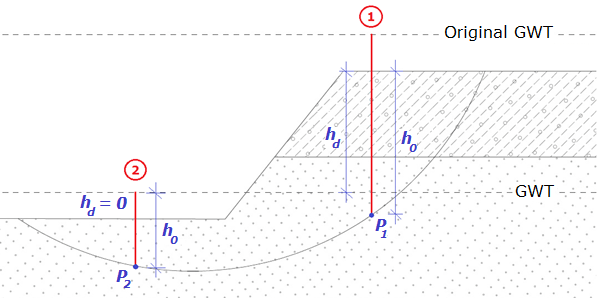 Análise de rebaixamento rápido
Análise de rebaixamento rápido
![]()
| onde: | h0 | – | distância vertical entre o nível freático original e o ponto em análise P |
| γw | – | peso volúmico da água |
![]()
| onde: | hd | – | distância entre os níveis freáticos original e atual |
| γw | – | peso volúmico da água |
![]()
| onde: | u0 | – | pressão nos poros inicial |
| X | – | coeficiente de redução da pressão nos poros inicial | |
| Δu | – | variação da pressão nos poros |
4) Coeficiente de pressão nos poros Ru
O coeficiente de pressão nos poros Ru representa o rácio entre a pressão nos poros e a pressão geostática no solo. Na área onde Ru é positivo, é considerado o peso volúmico saturado do solo γsat; caso contrário é considerado o peso volúmico do solo γ. Os valores de Ru são introduzidos através de isolinhas que unem pontos com o mesmo valor de Ru. É assumida interpolação linear para calcular valores intermédios. A pressão nos poros é estabelecida como tensão geostática sendo reduzida pelo coeficiente Ru:![]()
| onde: | Ru | – | coeficiente de pressão nos poros |
| hi | – | altura da iésima camada do solo | |
| γi | – | peso volúmico da iésima camada do solo |
5) Valores da pressão nos poros
O nível freático pode ser introduzido diretamente através dos valores da pressão nos poros u dentro da secção do perfil do solo. Na área em que u é positivo, é considerado o peso volúmico saturado do solo γsat; caso contrário, é considerado o peso volúmico do solo γ. Os valores das pressões nos poros são introduzidos através de isolinhas que unem os pontos com os mesmos valores de pressão nos polos. Valores intermédios são estimados a partir de interpolação linear. Os valores para a pressão nos poros é derivada a partir de valores para pontos específicos do talude.Sobrecarga
A análise de estabilidade de taludes considera as sobrecargas geradas por estruturas existentes nas proximidades. As sobrecargas podem ser introduzidas como cargas concentradas ou cargas distribuídas, atuantes na superfície do solo ou em camadas interiores.
Dado que é assumido que as sobrecargas são causadas pelo peso de elementos presentes na face do talude, a componente vertical da sobrecarga que tem a direção do peso (componente material) é adicionada ao seu peso próprio. Isto significa que se os efeitos sísmicos estiverem incluídos, esta componente também é multiplicada pelos fatores de aceleração horizontal e vertical do sismo. A componente material das sobrecargas também influencia a posição do centroide do bloco. O peso das componentes que não atuam na direção do peso é assumido em equações de equilíbrio, para um dado bloco, como nulo, sendo que não irá contribuir para momentos de inércia de sismo nem para a posição do centroide do bloco.
A análise considera sempre as sobrecargas com um metro de desenvolvimento. Fazendo com que as sobrecargas que atuam numa área b*l e que são introduzidas com forças concentradas, sejam modificadas, antes da análise, para forças superficiais que se estendem até à profundidade da superfície de deslizamento com um rácio de inclinação 2:1, como mostra a figura.
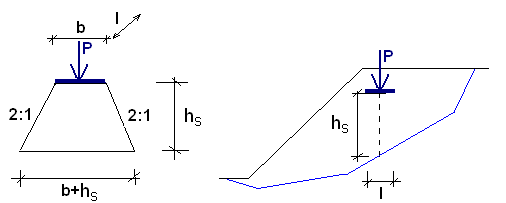 Esquema de distribuição de cargas concentradas na superfície de deslizamento
Esquema de distribuição de cargas concentradas na superfície de deslizamento
A análise considera a resultante da força superficial p, calculada através da equação:
![]()
Também é possível considerar um tipo especial de sobrecarga – água acima da superfície do terreno.
Massa de Água acima da Superfície do Terreno
Uma massa de água cima da superfície do terreno consiste num tipo de sobrecarga especial, que permite modelar níveis freáticos que não intersectam o maciço do solo. Isto é típico em reservatórios de água que estão separados do maciço do solo por membranas impermeáveis.
Neste caso, o nível freático atua de forma perpendicular à superfície do terreno, como uma sobrecarga de pressão hidrostática.
Tipo de sobrecarga “Água acuma do terreno”
O nível freático é representado por um ponto de coordenadas [x, z]. O programa considera a presença de água dentro de uma área rodeada pelo terreno ou pelas extremidades da tarefa e intersetadas por pontos definidos.
Não é correto considerar a influência normal da água dentro da área onde o nível freático está definido como uma sobrecarga. Neste caso, o programa mostra um aviso na análise e no relatório final. O aviso também é exibido caso duas ou mais sobrecargas de “água acima do terreno” atuem nos mesmos pontos do terreno.
 Aviso para sobreposição do nível freático
Aviso para sobreposição do nível freático
Ancoragens
A posição das ancoragens é definida pela posição da cabeça, comprimento livre l, comprimento ancorado lk e inclinação α. A força de ancorarem é introduzida como força de pré-esforço atuante na ancoragem. A cabeça da ancoragem está sempre localizada na superfície do terreno; a força da ancoragem atua sempre na direção do solo. Ao calcular o equilíbrio No cálculo do equilíbrio de um bloco, a força de ancoragem é somada à sobrecarga sem peso do talude.
Estão disponíveis duas formas para considerar ancoragens:
- Comprimento de ancoragens computados – a análise assume um comprimento infinito para as ancoragens (as ancoragens são sempre consideradas na análise) e calcula o seu comprimento livre (distância entre a cabeça e o troço ancorado) consequentemente. O troço ancorado situa-se atrás da superfície de deslizamento. Este método é utilizado sempre que seja pretendido o uso de ancoragens para aumentar a estabilidade do talude e se pretenda saber qual o comprimento mínimo das ancoragens.
- Análise com comprimento de ancoragens definido – a análise apenas considera as ancoragens que tenham o troço ancorado atrás da superfície de deslizamento. Se a superfície de deslizamento intercetar o comprimento livre da ancoragem, o cálculo considera a força total de ancoragem. Quando a superfície de deslizamento interseta o troço ancorado, a força da ancoragem é reduzido linearmente, com a força total para o início do troço ancorado e zero para o final. Este método é utilizado sempre que se pretenda avaliar o estado atual do talude, com ancoragens já existentes, uma vez que pode ser verificado que algumas ancoragens não possuam o comprimento necessário para intersetar a superfície de deslizamento crítica, não contribuindo para o aumento da estabilidade do talude.
Grampos
Para cada grampo, as seguintes capacidades de suporte podem ser introduzidas ou computadas:| onde: | Rf | – | resistência da cabeça do grampo |
| Rt | – | resistência à tensão | |
| Tp | – | resistência à compressão |
![]()
| onde: | Rt | – | resistência à tração |
| ds | – | diâmetro do grampo | |
| fy | – | resistência do material do grampo |
![]()
| onde: | Tp | – | resistência à tração do grampo [kN/m] |
| d | – | diâmetro do buraco | |
| gs | – | força de ligação máxima, dada como parâmetro do grampo ou do solo |
![]()
![]()
| onde: | Tp | – | resistência à tração do grampo [kN/m] |
| d | – | diâmetro do buraco | |
| σz | – | tensão geostática vertical | |
| φ | – | ângulo de atrito interno efetivo do solo | |
| c | – | coesão efetiva do solo |
![]()
| onde: | Tp | – | resistência à tração do grampo [kN/m] |
| d | – | diâmetro do buraco | |
| σn | – | tensão horizontal efetiva média | |
| φ | – | ângulo de atrito interno efetivo do solo | |
| c | – | coesão efetiva do solo |
![]()
| onde: | σz | – | tensão vertical geostática |
![]()
![]()
Reforços
Os reforços são elementos horizontais, inseridos no solo para aumentar a estabilidade de taludes através da resistência à tensão. Caso os reforços intersetem a superfície de deslizamento, a resistência gerada pelo reforço entra na equação de equilíbrio de um dado bloco em análise. Caso contrário, a estabilidade do talude não é influenciada. O parâmetro base para os reforços é a resistência à tração Rt. É utilizado um valor de dimensionamento para este parâmetro – isto é, a força do reforço reduzida por coeficientes que consideram os efeitos da durabilidade, deformação e danos causados durante a instalação. A força transmitida pelo reforço nunca pode exceder a resistência à tração definida Rt.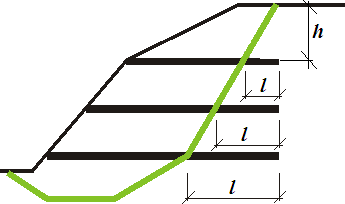 Esquema do posicionamento de reforços
Esquema do posicionamento de reforços
1) Cálculo da capacidade de carga do reforço
A força de tração F é dada por:![]()
| onde: | σ | – | tensão normal devido ao peso próprio na interseção do reforço e da superfície de deslizamento – ver Fig. |
| φ | – | ângulo de atrito interno do solo | |
| C | – | coeficiente de interação (0,8 assumido como valor padrão) | |
| l | – | comprimento da junta do reforço inserida no solo atrás da superfície de deslizamento |
2) Introdução do comprimento de ancoragem do reforço lk
É definido um comprimento de ancoragem lk. Este parâmetro é determinado pela força de cisalhamento desenvolvida entre o reforço e o solo, que aumenta gradualmente de zero até ao seu valor limite (medido a partir do final do troço do reforço inserido no solo).![]()
| onde: | l | – | comprimento do reforço inserido no solo atrás da superfície de deslizamento |
| lk | – | comprimento ancorado do reforço | |
| Rt | – | resistência à tensão |
3) Introdução da resistência à tração Tp
A força de tração F é dada por:![]()
| onde: | l | – | comprimento do reforço inserido no solo atrás da superfície de deslizamento |
| Tp | – | resistência à tração do reforço |
Posição dos Reforços
O programa permite que os suportes dos reforços sejam fixos ou livres.
Caso um talude que contenha reforços colapse, verificar-se-á um dos tipos de falha para reforços presentes nas figuras.
Caso o suporte inicial do reforço, à frente da superfície de deslizamento, esteja fixo (por exemplo, fixo ao revestimento da estrutura) o 3º tipo de falha é evitado – remoção do reforço à frente da superfície de deslizamento. As falhas do tipo 1 e 2 são sempre verificadas na análise, a falha do tipo 3 só é verificada se os suportes dos reforços sejam livres, permitindo que este tipo de falha ocorra.
 Caixa de diálogo “Novo reforço” – definir a posição do reforço
Caixa de diálogo “Novo reforço” – definir a posição do reforço
 Quebra do reforço – falha do tipo 1
Quebra do reforço – falha do tipo 1
 Remoção do reforço por trás da superfície de deslizamento – falha do tipo 2
Remoção do reforço por trás da superfície de deslizamento – falha do tipo 2
 Remoção do reforço à frente da superfície de deslizamento – falha do tipo 3
Remoção do reforço à frente da superfície de deslizamento – falha do tipo 3
Influência Sísmica
O programa permite calcular a influência sísmica de acordo com as seguintes normas:
![]() Análise padrão
Análise padrão
![]() Análise sísmica de acordo com a norma chinesa GB 50111-2006
Análise sísmica de acordo com a norma chinesa GB 50111-2006
![]() Análise sísmica de acordo com a norma chinesa NB 35047-2015
Análise sísmica de acordo com a norma chinesa NB 35047-2015
![]() Análise sísmica de acordo com a norma chinesa GB 50330-2013
Análise sísmica de acordo com a norma chinesa GB 50330-2013
![]() Análise sísmica de acordo com a norma chinesa JTG B02-2013
Análise sísmica de acordo com a norma chinesa JTG B02-2013
A vantagem das normas chinesas é que ao estabelecer a intensidade do sismo, o programa atribui automaticamente os valores respetivos do coeficiente Kh.
Efeitos Sísmicos – Análise Padrão
O programa permite computar os efeitos de um sismo com a ajuda de duas variáveis – coeficiente sísmico horizontal Kh ou o coeficiente sísmico vertical Kv.Coeficiente sísmico vertical Kv
O coeficiente sísmico vertical pode diminuir (Kv > 0) ou aumentar (Kv < 0) o peso volúmico do solo, da água presente no solo e da sobrecarga material, multiplicando os valores respetivos por 1 – Kv. É necessário ter em atenção que o coeficiente Kv pode assumir valores positivos ou negativos e no caso do coeficiente de aceleração horizontal ser suficientemente elevado o alívio do talude (Kv > 0) é mais desfavorável que a sobrecarga.Coeficiente sísmico horizontal Kh
Geralmente, a computação é executada assumindo o valor de zero para o coeficiente sísmico horizontal Kh. No entanto, esta constante pode ser explorada para simular o efeito de um sismo. Este valor representa o rácio entre as acelerações gravítica e horizontal. Aumentar o coeficiente Kh leva a uma redução proporcional do fator de segurança FS. O coeficiente sísmico horizontal introduz uma força horizontal à análise, atuante no centro de gravidade do bloco em estudo, com uma magnitude de Kh*Wi, onde Wi é o peso total do bloco, incluindo a componente material e a sobrecarga do talude. A tabela seguinte apresenta a lista dos valores para o coeficiente sísmico Kh de acordo com a escala de Mercalli-Cancani-Sieberg (MCS).| Escala MCS | Aceleração horizontal | Coeficiente sísmico horizontal | ||||||
| (MSK-64) | [mm/s2] | Kh | ||||||
| 1 | 0,0 | – | 2,5 | 0,0 | – | 0.00025 | ||
| 2 | 2,5 | – | 5,0 | 0,00025 | – | 0.0005 | ||
| 3 | 5,0 | – | 10,0 | 0,0005 | – | 0.001 | ||
| 4 | 10,0 | – | 25,0 | 0,001 | – | 0.0025 | ||
| 5 | 25,0 | – | 50,0 | 0,0025 | – | 0.005 | ||
| 6 | 50,0 | – | 100,0 | 0,005 | – | 0.01 | ||
| 7 | 100,0 | – | 250,0 | 0,01 | – | 0.025 | ||
| 8 | 250,0 | – | 500,0 | 0,025 | – | 0.05 | ||
| 9 | 500,0 | – | 1000,0 | 0,05 | – | 0.1 | ||
| 10 | 1000,0 | – | 2500,0 | 0,1 | – | 0.25 | ||
| 11 | 2500,0 | – | 5000,0 | 0,25 | – | 0.5 | ||
| 12 | > | 5000,0 | > | 0.5 | ||||
Earthquake Analysis According to GB 50111-2006
Earthquake effects are in stability analysis represented by horizontal and vertical forces acting at the centers of gravity of individual soil blocks. Magnitude of these forces is related to the weight of soil blocks and is calculated using horizontal and vertical earthquake coefficients. Horizontal earthquake force is always oriented out form the slope massif. Vertical force can be directed upwards or downwards, the orientation is defined by the sign of the force. Horizontal earthquake force Ehs is given by formula:![]()
![]()
| where: | Ci | – | importance coefficient for seismic design |
| Cz | – | comprehensive influence factor | |
| C0 | – | meeting coefficient related to the influence of horizontal seismic effect | |
| Kh | – | coefficient of horizontal seismic acceleration | |
| Kv | – | coefficient of vertical seismic acceleration | |
| Gs | – | weight of the soil block |
Earthquake Analysis According to NB 35047-2015
Earthquake effects are in stability analysis represented by horizontal and vertical forces acting at the centers of gravity of individual soil blocks. Magnitude of these forces is related to the weight of soil blocks and is calculated using horizontal and vertical earthquake coefficients. Earthquake coefficients are depended on position gravity center of each block. Therefore the coefficients have individual and different values for each one of soil blocks. Horizontal earthquake force is always oriented out form the slope massif. Vertical force can be directed upwards or downwards, the orientation is defined by the sign of the force. Horizontal earthquake force Ehs is given by formula:![]()
![]()
| where: | Ci | – | importance coefficient for seismic design |
| Cz | – | comprehensive influence factor | |
| C0 | – | meeting coefficient related to the influence of horizontal seismic effect | |
| Kh | – | coefficient of horizontal seismic acceleration | |
| Kv | – | coefficient of vertical seismic acceleration | |
| Gs | – | weight of the soil block | |
| αi | – | dynamic distribution coefficient of block i |
There are two types of dynamic distribution used for determining of αi value: inverted trapezoid and polygonal. Method for setting αi value could be seen at Figure.
Determination of dynamic distribution coefficient αi
Earthquake Analysis According to GB 50330-2013
Earthquake effects are in stability analysis represented by horizontal and vertical forces acting at the centers of gravity of individual soil blocks. Magnitude of these forces is related to the weight of soil blocks and is calculated using horizontal and vertical earthquake coefficients. Horizontal earthquake force is always oriented out form the slope massif. Vertical force can be directed upwards or downwards, the orientation is defined by the sign of the force. Horizontal earthquake force Ehs is given by formula:![]()
![]()
| where: | Ci | – | importance coefficient for seismic design |
| αw | – | complex factor of horizontal acceleration | |
| ag | – | complex factor of vertical acceleration | |
| Gs | – | weight of the soil block |
Earthquake Analysis According to JTG B02-2013
Earthquake effects are in stability analysis represented by horizontal and vertical forces acting at the centers of gravity of individual soil blocks. Magnitude of these forces is related to the weight of soil blocks and is calculated using horizontal and vertical earthquake coefficients. Earthquake coefficients are depended on position gravity center of each block. Therefore the coefficients have individual and different values for each one of soil blocks. Horizontal earthquake force is always oriented out form the slope massif. Vertical force can be directed upwards or downwards, the orientation is defined by the sign of the force. Horizontal earthquake force Ehs is given by formula:![]()
![]()
| where: | Ci | – | importance coefficient for seismic design |
| Cz | – | comprehensive influence factor | |
| Kh | – | coefficient of horizontal seismic acceleration | |
| Kv | – | coefficient of vertical seismic acceleration | |
| Gs | – | weight of the soil block | |
| ψi | – | dynamic distribution coefficient of block i |
Method for setting ψi value could be seen at Figure.
Determination of dynamic distribution coefficient ψi
Height H of the range of ψi is given by points B and T. The bottom point B is the lowest point of terrain above the slip surface and the top point T is the highest point of terrain above the slip surface. Gi denotes gravity center points of individual blocks and Eih, Eiv are horizontal and vertical earthquake forces.Verificação de Acordo com EN 1997
Quando se executa a análise de verificação de acordo com EN 1997 a definição da “Abordagem do projeto” e dos “Fatores parciais” é importante. As forças e cargas são reduzidas em todas as aproximações. O valor da capacidade de utilização Vu é calculado e comparado com o valor a 100%. O valor da capacidade de utilização é dado por:![]()
| onde: | Ma | – | momento desestabilizador |
| Mp | – | momento resistente |
No caso da abordagem do projeto 2, o momento resistente Mp é determinado a partir de parâmetros do solo não reduzidos mas considerando a redução da resistência da superfície de deslizamento através do coeficiente γRs. Nos caos da abordagem do projeto 1 e da abordagem do projeto 3, o programa reduz os parâmetros de resistência do solo (ângulo de atrito interno e coesão) para determinar o momento resistente global Mp.
Análise de Acordo com a Teoria dos Estados Limite / Fator de Segurança
Os parâmetros de verificação são introduzidos na secção da “Análise de estabilidade”. A estrutura pode ser verificada de acordo com o fator de segurança ou com a teoria dos estados limite. Verificação de acordo com a teoria dos estados limite: Neste caso, os parâmetros do solo (ângulo de atrito interno, coesão) são reduzidos através dos coeficientes de dimensionamento introduzidos na secção “Análise de estabilidade”. O valor de utilização Vu é calculado e comparado com o valor a 100%. Este valor é dado por:![]()
| onde: | Ma | – | momento desestabilizador |
| Mp | – | momento resistente |
![]()
| onde: | Ma | – | momento desestabilizador |
| Mp | – | momento resistente | |
| SFs | – | fator de segurança |
Superfície de Deslizamento Poligonal
A resolução da estabilidade de taludes adotando uma superfície de deslizamento poligonal baseia-se na determinação do estado limite das forças atuantes no solo acima da superfície de deslizamento. Para introduzir estas forças a superfície de deslizamento os blocos em análise são divididos por planos. Normalmente estes planos são verticais, mas não é uma condição obrigatória, ex.: o método de Sarma considera planos inclinados.
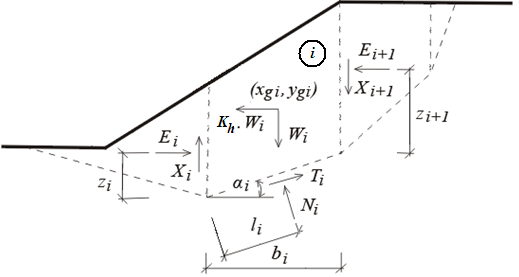 Esquema estático de um bloco
Esquema estático de um bloco
A figura mostra as forças atuantes em blocos do solo. Se a região acima da superfície de deslizamento for dividida em blocos, as incógnitas são: n forças normais Ni atuantes em segmentos individuais e que correspondem a n forças de cisalhamento Ti; n-1 forças normais entre blocos Ei e correspondentes n-1 forças de cisalhamentos Xi ; n-1 valores de zi que representa os pontos de aplicação das forças Ei, n valores de li que representa os pontos de aplicação das forças Ni e um valor do fator de segurança FS. Em alguns métodos, as forças Xi podem ser substituídas pelos valores da inclinação das forças Ei.
Os parâmetros conhecidos das equações de equilíbrio disponíveis são: n equações de equilíbrio horizontais e n equações de equilíbrio verticais para cada bloco, n momentos de equilíbrio para cada bloco e n relações entre as forças Ni e Ti desenvolvidas nos blocos de acordo com a teoria de Mohr-Coulomb. No total, existem 4n equações para 6n-2 incógnitas. Isto significa que 2n-2 incógnitas devem ser escolhidas previamente. Os métodos diferem quanto a forma de selecionar estes valores.
O mais comum é definir os pontos de aplicação de forças individuais atuantes entre blocos ou as suas inclinações. A resolução do problema de equilíbrio é através de iterações, onde os valores definidos devem permitir que tanto as condições de equilíbrio como de cinemática sejam satisfeitas para a solução obtida.
O programa permite adotar um dos seguintes métodos:
![]() Sarma
Sarma
![]() Spencer
Spencer
![]() Janbu
Janbu
![]() Morgenstern-Price
Morgenstern-Price
![]() Shahunyants
Shahunyants
![]() ITF Method
ITF Method
A otimização de superfícies de deslizamento poligonais procura a superfície mais crítica (o menor fator de segurança FS).
Sarma
O método de Sarma consiste num método geral de divisões dos estados limite. Este método baseia-se em completar as condições de equilíbrio dos momentos e forças que atuam em cada bloco. Os blocos são criados a partir da divisão da região do solo acima da potencial superfície de deslizamento, através de planos, que podem ter inclinações diferentes. A figura mostra as forças que atuam em cada bloco.
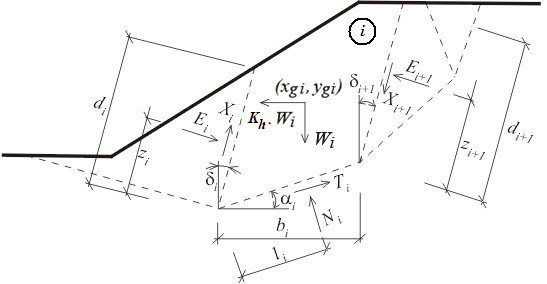 Esquema das forças atuantes – Método de Sarma
Esquema das forças atuantes – Método de Sarma
Aqui, Ei , Xi representam as forças normal e de cisalhamento entre blocos. Ni , Ti representam as forças normal e de cisalhamento nos segmentos da superfície de deslizamento. Wi representa o peso do bloco e Kh*Wi representa a força horizontal utilizada para atingir o estado limite no método de Sarma. Podem ser introduzidas sobrecargas inclinadas a cada bloco. Esta sobrecarga é incluída na análise juntamente com a sobrecarga devido ao nível freático, quando este se encontra acima do bloco em análise, e as forças das ancoragens. Estas forças são projetadas nas direções horizontal e vertical, sendo resumidas nas componentes Fxi e Fyi.
Kh é a constante que define o fator de aceleração horizontal e é introduzida na análise para satisfazer o equilíbrio de cada bloco. Existe uma relação entre o Kh e o fator de estabilidade do talude que permite que a computação do fator de segurança FS. Em situações normais, a análise é executada com o valor de Kh igual a zero. Um valor diferente de zero para Kh é utilizado para simular a sobrecarga horizontal, ex.: devido a um sismo (ver em baixo).
Processo da análise
Computação do equilíbrio limite
A computação do equilíbrio limite requer a resolução de 6n – 1 incógnitas, onde n representa o número de blocos que divide a região do solo acima da superfície de deslizamento potencial. Estas são:
| Ei | – | forças desenvolvidas entre blocos |
| Ni | – | forças normais atuantes na superfície de deslizamento |
| Ti | – | forças de cisalhamento atuantes na superfície de deslizamento |
| Xi | – | forças de cisalhamento desenvolvidas entre blocos |
| zi | – | localização dos pontos de aplicação de forças |
| li | – | localização dos pontos de aplicação de forças |
| Kh | – | fator de aceleração horizontal |
5n – 1 equações estão disponíveis para determinar as incógnitas. Em particular, temos:
a) equação de equilíbrio do bloco para as forças horizontais:
![]()
b) equação de equilíbrio do bloco para as forças verticais:
![]()
c) equação de equilíbrio do bloco para momentos:
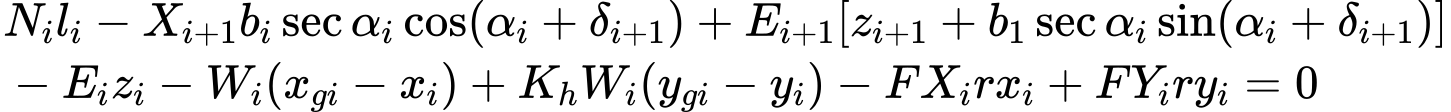
onde rxi e ryi representam o braço das forças Fxi e Fyi
d) relação entre as forças normal e de cisalhamento de acordo com a teoria de Mohr-Coulomb:
![]()
![]()
| onde: | P*Wi | – | força resultante da pressão nos poros dos planos divisores |
| – | valor médio do ângulo de atrito interno dos planos divisores | ||
| – | valor médio da coesão dos planos divisores |
É evidente que n – 1 devem ser selecionadas (estimadas) com prioridade. Existe um erro relativamente pequeno na estimativa dos pontos de aplicação das forças Ei. O problema passa a ser estaticamente determinado. Ao resolver o sistema de equações é possível determinar os valores de todas as incógnitas. O resultado principal desta análise é a determinação do fator de aceleração horizontal Kh.
Computação do fator de segurança da estabilidade do talude FS
O fator de segurança da estabilidade do talude FS é introduzido na análise de forma a reduzir os parâmetros c e tgφ do solo. A análise de equilíbrio é realizada de acordo com os parâmetros reduzidos do solo para obter um valor do fator horizontal de aceleração Kh que permita verificar a estabilidade do talude de acordo com o fator de segurança SF pretendido. Este cálculo é um processo iterativo que se repete até que o fator Kh seja igual a zero ou a um valor desejado.
Influência de cargas externas
O talude em análise pode ser carregado por forças trapezoidais inclinadas. Para a análise de estabilidade, estas cargas são consideradas de maneira a que a componente material vertical (caso possua a mesma direção que o peso) seja adicionada ao peso do bloco em estudo. Isto irá alterar o peso do bloco e a posição do seu centro de gravidade. Se a direção da componente vertical for inversa à da gravidade, o valor da componente vertical será adicionado à força Fyi. A componente horizontal é adicionada à força Fxi.
Bibliografia:
Sarma, S. K.: Stability analysis of embankments and slopes, Géotechnique 23, 423-433, 1973.
Spencer
O método de Spencer baseia-se na análise do estado de equilíbrio limite, considerando a divisão do perfil do talude em blocos. Este método implica a verificação de equilíbrio para as forças e momentos que atuam em cada bloco. Os blocos consistem em divisões do perfil do talude, por planos. A figura seguinte mostra as forças que atuam em cada bloco.
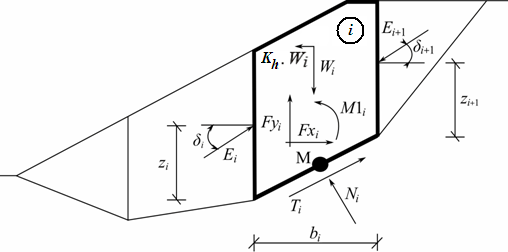 Esquema das forças atuantes – Método de Spencer
Esquema das forças atuantes – Método de Spencer
Cada bloco estará sujeito às forças seguintes:
| Wi | – | peso do bloco, incluindo o valor da componente material vertical de sobrecargas com direção descendente, considerando a influência do coeficiente sísmico vertical Kv |
| Kh*Wi | – | momento de inércia horizontal considerando o efeito sísmico, onde Kh é o coeficiente sísmico horizontal |
| Ni | – | força normal atuante na superfície do talude |
| Ti | – | força de cisalhamento atuante na superfície do talude |
| Ei ,Ei+1 | – | forças exercidas por blocos vizinhos, com um ângulo de inclinação δ medido a partir do plano horizontal |
| Fxi,Fyi | – | outras forças horizontais e verticais atuantes no bloco |
| M1i | – | momentos das forças Fxi, Fyi em relação ao ponto M, que representa o centro do iésimo segmento da superfície de deslizamento |
| Ui | – | empuxo resultante no iésimo segmento da superfície de deslizamento |
No cálculo do equilíbrio limite de forças e momentos de cada bloco através do método de Spencer, são assumidas as seguintes premissas:
![]() os planos que divisores dos blocos são sempre verticais
os planos que divisores dos blocos são sempre verticais
![]() a linha de ação do peso do bloco Wi atravessa o centro do iésimo segmento da superfície de deslizamento, representado pelo ponto M
a linha de ação do peso do bloco Wi atravessa o centro do iésimo segmento da superfície de deslizamento, representado pelo ponto M
![]() a força normal Ni atua no centro do iésimo segmento da superfície de deslizamento, representado pelo ponto M
a força normal Ni atua no centro do iésimo segmento da superfície de deslizamento, representado pelo ponto M
![]() a inclinação das forças Ei que atuam entra blocos é constante para todos os blocos e é igual a δ, com δ = 0 apenas nos pontos limite da superfície de deslizamento
a inclinação das forças Ei que atuam entra blocos é constante para todos os blocos e é igual a δ, com δ = 0 apenas nos pontos limite da superfície de deslizamento
A solução assenta nas seguintes equações:
| (1) | |
| (2) | |
| (3) | |
| (4) | |
| (5) |
| onde: | φi | – | ângulo de atrito interno do solo no segmento da superfície de deslizamento |
| ci | – | coesão do solo no segmento da superfície de deslizamento | |
| αi | – | inclinação do segmento da superfície de deslizamento |
A Equação (1) representa a relação entre os valores efetivo e total da força normal atuante na superfície de deslizamento. A Equação (2) corresponde à condição de Mohr-Coulomb que representa a relação entre as forças normal e de cisalhamento para um dado segmento da superfície de deslizamento. A Equação (3) representa a equação de equilíbrio de forças com direção normal ao iésimo segmento da superfície de deslizamento, enquanto que a Equação (4) representa o equilíbrio de forças com a direção do iésimo segmento da superfície de deslizamento. FS é o fator de segurança, que é utilizado para reduzir os valores das características do solo. A Equação (5) corresponde à equação de equilíbrio de momentos no ponto M, onde ygi é a coordenada vertical do ponte de aplicação do peso do bloco e yM é a coordenada vertical do ponto M. A partir das Equações (3) e (4) obtém-se a seguinte equação:
Esta fórmula permite calcular todas as forças Ei que atuam entre blocos, para os valores de δi e FS considerados. Esta solução assume que o valor de E para a origem da superfície de deslizamento é conhecido e igual a E1 = 0.
A partir da Equação (5) de equilíbrio de momentos obtém-se a seguinte equação:
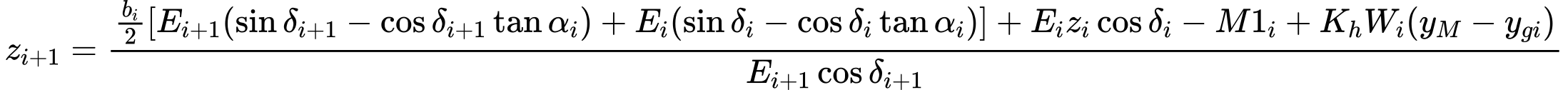
Esta equação permite calcular, para um dado valor de δ, todos os braços z das forças atuantes entre blocos, conhecendo o valor à esquerda da origem da superfície de deslizamento, onde z1 = 0.
O fator de segurança FS é determinado através do seguinte processo iterativo:
- O valor inicial de δ é definido como zero δ = 0.
- O fator de segurança FS para um dado valor de δ é obtido a partir da Equação (6), assumindo o valor de En+1 = 0 no limite da superfície de deslizamento.
- O valor de δ é obtido através da Equação (7) considerando os valores de E determinados no passo anterior, respeitando a condicionante do momento no último bloco ser zero. A Equação (7) não permite obter o valor de zn+1, uma vez que este é igual a zero. Para este valor, a Equação (5) de equilíbrio de momentos deve ser verificada.
- Os passos 2 e 3 são repetidos até que o valor de δ deixe de variar.
Para que o processo iterativo estabilize, é necessário evitar soluções instáveis. Estas instabilidades podem ocorrer quando se verificarem divisões por zero nas Equações (6) e (7). Na Equação (7), a divisão por zero verifica-se quando δ = π/2 ou δ = -π/2. Assim, o valor do ângulo δ deve estar compreendido no intervalo (-π/2 ; π/2).
Na Equação (6), a divisão por zero verifica-se quando:
![]()
Outra verificação que deve ser verificada para prevenir a instabilidade numérica é a do parâmetro mα – a seguinte condição deve ser verificada:
![]()
Assim, antes de iniciar o processo iterativo, é necessário obter o valor mais crítico FSmin que satisfaça todas as condições referidas. Os valores inferiores a este valor crítico FSmin representam soluções instáveis, sendo que o processo iterativo terá início com a definição de FS como um valor imediatamente acima de FSmin e, consequentemente, todos os valores de FS do processo iterativo serão superiores a FSmin.
Geralmente, a convergência de métodos rigorosos é pior que a de métodos mais simples (Bishop, Fellenius). Como exemplos, os problemas de convergência podem ser encontrados para secções demasiado inclinadas de superfícies de deslizamento, geometrias complexas, variações de sobrecargas elevadas, etc. Caso não seja obtido nenhum resultado, é recomendável uma ligeira alteração nos dados introduzidos, ex.: inclinação da superfície de deslizamento menos acentuada, introduzir mais pontos na superfície de deslizamento, etc, ou recorrer a métodos mais simples.
Bibliografia:
Spencer, E. 1967. A method of analysis of the stability of embankments assuming parallel interslice forces. Géotechnique, 17(1): 11-26.
Janbu
O método de Janbu baseia-se na análise do estado de equilíbrio limite. Este método implica que o equilíbrio de forças e momentos seja verificada para cada bloco (excluindo o bloco superior, onde o equilíbrio de momentos não é verificado). Os blocos consistem na divisão do perfil do talude através de planos divisores. As forças atuam em cada bloco de acordo com a seguinte figura:
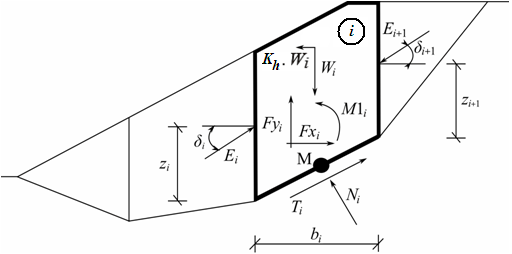 Esquema das forças atuantes – Método de Janbu
Esquema das forças atuantes – Método de Janbu
Cada bloco estará sujeito às forças seguintes:
| Wi | – | peso do bloco, incluindo o valor da componente material vertical de sobrecargas com direção descendente, considerando a influência do coeficiente sísmico vertical Kv |
| Kh*Wi | – | momento de inércia horizontal considerando o efeito sísmico, onde Kh é o coeficiente sísmico horizontal |
| Ni | – | força normal atuante na superfície do talude |
| Ti | – | força de cisalhamento atuante na superfície do talude |
| Ei ,Ei+1 | – | forças exercidas por blocos vizinhos, com um ângulo de inclinação δi e δi+1, respetivamente, medido a partir do plano horizontal e à cota zi e zi+1, respetivamente, acima da superfície de deslizamento |
| Fxi,Fyi | – | outras forças horizontais e verticais atuantes no bloco |
| M1i | – | momentos das forças Fxi, Fyi em relação ao ponto M, que representa o centro do iésimo segmento da superfície de deslizamento |
| Ui | – | empuxo resultante no iésimo segmento da superfície de deslizamento |
Para calcular o equilíbrio de forças e momentos limite através do método de Janbu, são consideradas as seguintes premissas:
![]() os planos que divisores dos blocos são sempre verticais
os planos que divisores dos blocos são sempre verticais
![]() a linha de ação do peso do bloco Wi atravessa o centro do iésimo segmento da superfície de deslizamento, representado pelo ponto M
a linha de ação do peso do bloco Wi atravessa o centro do iésimo segmento da superfície de deslizamento, representado pelo ponto M
![]() a força normal Ni atua no centro do iésimo segmento da superfície de deslizamento, representado pelo ponto M
a força normal Ni atua no centro do iésimo segmento da superfície de deslizamento, representado pelo ponto M
![]() a posição zi das forças Ei atuantes entre blocos é para os limites da superfície de deslizamento é assumida como z = 0
a posição zi das forças Ei atuantes entre blocos é para os limites da superfície de deslizamento é assumida como z = 0
A escolha da posição zi pode influenciar significativamente a convergência do método. Caso seja adotada uma má posição zi para um dado talude, poderá ser impossível verificar as condições de equilíbrio (algoritmo não convergente). As alturas zi acima da superfície de deslizamento são definidas para aproximadamente um terço da altura da interface entre blocos. No caso das condições de equilíbrio não serem satisfeitas, o algoritmo altera as alturas, ex.: ligeiramente acima, dentro da zona passiva, próximo da base do talude; ligeiramente abaixo, dentro da zona ativa, próximo do topo do talude.
A solução assenta nas seguintes equações:
| (1) | |
| (2) | |
| (3) |
| (4) |
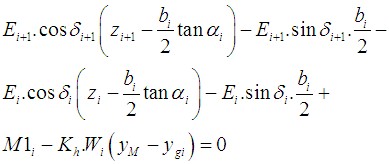 | (5) |
| onde: | φi | – | ângulo de atrito interno do solo no segmento da superfície de deslizamento |
| ci | – | coesão do solo no segmento da superfície de deslizamento | |
| αi | – | inclinação do segmento da superfície de deslizamento |
A Equação (1) representa a relação entre os valores efetivo e total da força normal atuante na superfície de deslizamento. A Equação (2) corresponde à condição de Mohr-Coulomb que representa a relação entre as forças normal e de cisalhamento para um dado segmento da superfície de deslizamento. A Equação (3) representa a equação de equilíbrio de forças com direção normal ao iésimo segmento da superfície de deslizamento, enquanto que a Equação (4) representa o equilíbrio no iésimo segmento da superfície de deslizamento. FS é o fator de segurança, que é utilizado para reduzir os valores das características do solo. A Equação (5) corresponde à equação de equilíbrio de momentos em relação ao ponto M, onde ygi é a coordenada vertical do ponte de aplicação do peso do bloco e yM é a coordenada vertical do ponto M.
A partir das Equações (3) e (4) obtém-se a seguinte equação:
| (6) |
Esta fórmula permite calcular todas as forças Ei que atuam entre blocos, para os valores de δi e FS considerados. Esta solução assume que o valor de E para a origem da superfície de deslizamento é conhecido e igual a E1 = 0.
A partir da Equação (5) de equilíbrio de momentos obtém-se a seguinte Equação (7), para calcular os ângulos δi:
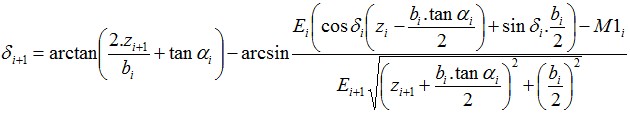 | (7) |
Esta equação permite calcular, para um dado valor de δ, todos os braços zi das forças atuantes entre blocos, conhecendo o valor à esquerda da origem da superfície de deslizamento, onde z1 = 0.
O fator de segurança FS é determinado através do seguinte processo iterativo:
- O valor inicial para os ângulos é definido como zero δi = 0 e as posições zi como aproximadamente um terço da altura da interface.
- O fator de segurança FS para um dado valor de δi é obtido através da Equação (6), assumindo o valor de En+1 = 0 para o limite da superfície de deslizamento.
- O valor de δi é obtido através da Equação (7), considerando os valores de Ei determinados no passo anterior.
- O passos 2 e 3 são repetidos até que o valor de FS não se altere.
É necessário evitar soluções instáveis para que o processo iterativo seja bem sucedido. As instabilidade podem ocorrer quando existem divisões por zero na Equação (6):
![]()
Outra verificação que deve ser verificada para prevenir a instabilidade numérica é a do parâmetro mα – a seguinte condição deve ser verificada:
![]()
Assim, antes de iniciar o processo iterativo, é necessário obter o valor mais crítico FSmin que satisfaça todas as condições referidas. Os valores inferiores a este valor crítico FSmin representam soluções instáveis, sendo que o processo iterativo terá início com a definição de FS como um valor imediatamente acima de FSmin e, consequentemente, todos os valores de FS do processo iterativo serão superiores a FSmin.
Geralmente, a convergência de métodos rigorosos é pior que a de métodos mais simples (Bishop, Fellenius). Como exemplos, os problemas de convergência podem ser encontrados para secções demasiado inclinadas de superfícies de deslizamento, geometrias complexas, variações de sobrecargas elevadas, etc. Caso não seja obtido nenhum resultado, é recomendável uma ligeira alteração nos dados introduzidos, ex.: inclinação da superfície de deslizamento menos acentuada, introduzir mais pontos na superfície de deslizamento, etc, ou recorrer a métodos mais simples.
Bibliografia:
Janbu, N. 1954. Application of Composite Slip Surface for Stability Analysis. European Conference on Stability Analysis, Stockholm, Sweden.
Janbu, N. 1973. Slope Stability Computations. Embankment Dam Engineering – Casagrande Volume, R.C. Hirschfeld and S.J. Poulos, eds., John Wiley and Sons, New York, pp 47-86.
Morgenstern-Price
O método de Morgenstern-Price baseia-se na análise do estado de equilíbrio limite. Este método implica que o equilíbrio de forças e momentos seja verificada para cada bloco (excluindo o bloco superior, onde o equilíbrio de momentos não é verificado). Os blocos consistem na divisão do perfil do talude através de planos divisores. As forças atuam em cada bloco de acordo com a seguinte figura:
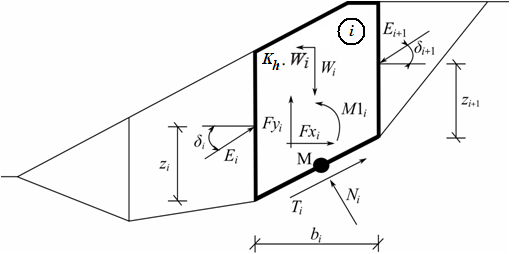 Esquema das forças atuantes – Método de Morgenstern-Price
Esquema das forças atuantes – Método de Morgenstern-Price
O contributo das forças em cada bloco é igual ao assumido no método de Spencer. Para calcular o equilíbrio de forças e momentos limite através do método de Morgenstern-Price, são consideradas as seguintes premissas:
![]() os planos que divisores dos blocos são sempre verticais
os planos que divisores dos blocos são sempre verticais
![]() a linha de ação do peso do bloco Wi atravessa o centro do iésimo segmento da superfície de deslizamento, representado pelo ponto Ma força normal Ni atua no centro do iésimo segmento da superfície de deslizamento, representado pelo ponto M
a linha de ação do peso do bloco Wi atravessa o centro do iésimo segmento da superfície de deslizamento, representado pelo ponto Ma força normal Ni atua no centro do iésimo segmento da superfície de deslizamento, representado pelo ponto M
![]() a inclinação das forças Ei atuantes entre blocos é diferente para cada bloco (δi), com δ = 0 nos pontos limite da superfície de deslizamento
a inclinação das forças Ei atuantes entre blocos é diferente para cada bloco (δi), com δ = 0 nos pontos limite da superfície de deslizamento
A única diferença entre os métodos de Spencer e de Morgenstern-Price está demonstrado na lista de premissas acima descrita. A escolha dos ângulos de inclinação δi das forças Ei atuantes entre blocos é efetuada com base numa função semi-senoidal – uma das funções da figura seguinte é automaticamente selecionada. A escolha da forma da função tem uma influência mínima nos resultados finais, mas a escolha da forma mais adequada pode melhorar a convergência do método. O valor da função semi-senoidal f(xi) para os pontos fronteira xi multiplicado pelo parâmetro λ resulta no valor do ângulo de inclinação δi.
 Função semi-senoidal
Função semi-senoidal
A solução assenta nas Equações (1) – (5), demostradas para o método de Spencer:
| (1) | |
| (2) | |
| (3) |
| (4) |
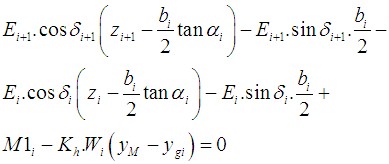 | (5) |
| onde: | φi | – | ângulo de atrito interno do solo no segmento da superfície de deslizamento |
| ci | – | coesão do solo no segmento da superfície de deslizamento | |
| αi | – | inclinação do segmento da superfície de deslizamento |
![]() (1) relação entre os valores efetivo e total da força normal atuante na superfície de deslizamento
(1) relação entre os valores efetivo e total da força normal atuante na superfície de deslizamento
![]() (2) condição de Mohr-Coulomb que representa a relação entre as forças normal e de cisalhamento para um dado segmento da superfície de deslizamento (Ni a Ti)
(2) condição de Mohr-Coulomb que representa a relação entre as forças normal e de cisalhamento para um dado segmento da superfície de deslizamento (Ni a Ti)
![]() (3) equação de equilíbrio de forças na direção normal ao iésimo segmento da superfície de deslizamento
(3) equação de equilíbrio de forças na direção normal ao iésimo segmento da superfície de deslizamento
![]() (4) equação de equilíbrio de forças na direção do iésimo segmento da superfície de deslizamento
(4) equação de equilíbrio de forças na direção do iésimo segmento da superfície de deslizamento
![]() (5) equação de equilíbrio de momentos no ponto M
(5) equação de equilíbrio de momentos no ponto M
A partir das Equações (3) e (4) obtém-se a Equação (6):
| (6) |
Esta fórmula permite calcular todas as forças Ei que atuam entre blocos, para os valores de δi e FS considerados. Esta solução assume que o valor de E para a origem da superfície de deslizamento é conhecido e igual a E1 = 0.
A partir da Equação (5) de equilíbrio de momentos obtém-se a Equação (7):
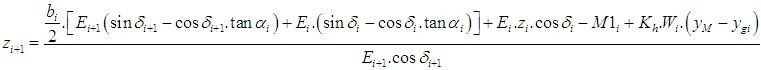 | (7) |
Esta equação permite calcular todos os braços zi das forças atuantes entre blocos, de acordo com os valores de δi, conhecendo o valor à esquerda da origem da superfície de deslizamento, onde z1 = 0.
O fator de segurança FS é determinado através do seguinte processo iterativo:
- O valor inicial dos ângulos δi é definido de acordo com a função semi-senoidal (δi = λ*f(xi)).
- O fator de segurança FS para um dado valor de δi é obtido a partir da Equação (6), assumindo que o valor de En+1 = 0 para os limites da superfície de deslizamento.
- O valor de δi é obtido através da Equação (7) considerando os valores de Ei determinados no passo anterior, respeitando a condição do momento ser nulo no último bloco. Os valores da função f(xi) são constantes durante todo o processo iterativo, sendo que apenas o parâmetro λ é iterado. A Equação (7) não calcula o valor de zn+1 dado que este é nulo. Para este valor, a Equação (5) de equilíbrio de momentos deve ser verificada.
- Os passos 2 e 3 são repetidos até que o valor de δi (e o respetivo parâmetro λ) não se alterem.
Para que o processo iterativo estabilize, é necessário evitar soluções instáveis. Estas instabilidades podem ocorrer quando se verificarem divisões por zero nas Equações (6) e (7). Na Equação (7), a divisão por zero verifica-se quando δ = π/2 ou δ = -π/2. Assim, o valor do ângulo δ deve estar compreendido no intervalo (-π/2 ; π/2).
Na Equação (6), a divisão por zero verifica-se quando:
![]()
Outra verificação que deve ser verificada para prevenir a instabilidade numérica é a do parâmetro mα – a seguinte condição deve ser verificada:
![]()
Assim, antes de iniciar o processo iterativo, é necessário obter o valor mais crítico FSmin que satisfaça todas as condições referidas. Os valores inferiores a este valor crítico FSmin representam soluções instáveis, sendo que o processo iterativo terá início com a definição de FS como um valor imediatamente acima de FSmin e, consequentemente, todos os valores de FS do processo iterativo serão superiores a FSmin.
Geralmente, a convergência de métodos rigorosos é pior que a de métodos mais simples (Bishop, Fellenius). Como exemplos, os problemas de convergência podem ser encontrados para secções demasiado inclinadas de superfícies de deslizamento, geometrias complexas, variações de sobrecargas elevadas, etc. Caso não seja obtido nenhum resultado, é recomendável uma ligeira alteração nos dados introduzidos, ex.: inclinação da superfície de deslizamento menos acentuada, introduzir mais pontos na superfície de deslizamento, etc, ou recorrer a métodos mais simples.
Bibliografia:
Morgenstern, N.R., and Price, V.E. 1965. The analysis of the stability of general slip surfaces. Géotechnique, 15(1): 79-93.
Morgenstern, N.R., and Price, V.E. 1967. A numerical method for solving the equations of stability of general slip surfaces. Computer Journal, 9: 388-393.
Zhu, D.Y., Lee, C.F., Qian, Q.H., and Chen, G.R. 2005. A concise algorithm for computing the factor of safety using the Morgenstern-Price method. Canadian Geotechnical Journal, 42(1): 272-278.
Shahunyants
O método de Shahunyants baseia-se na análise do estado de equilíbrio limite. Este método implica que o equilíbrio de forças e momentos seja verificada para cada bloco (excluindo o bloco superior, onde o equilíbrio de momentos não é verificado). Os blocos consistem na divisão do perfil do talude através de planos divisores. As forças atuam em cada bloco de acordo com a seguinte figura:
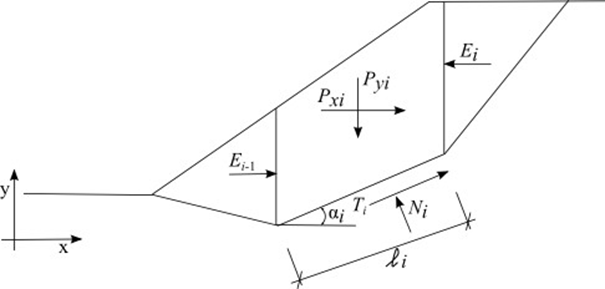 Esquema das forças atuantes – Método de Shahunyants
Esquema das forças atuantes – Método de Shahunyants
Cada bloco estará sujeito às forças seguintes:
| onde: | Pyi | – | resultante das forças verticais atuantes em cada bloco (peso do bloco, sobrecarga, ação sísmica, forças de ancoragens, …) |
| Pxi | – | resultante das forças horizontais atuantes em cada bloco (sobrecarga, ação sísmica, forças de ancoragens, geo-reforços, …) | |
| Ei+1, Ei | – | forças desenvolvidas entre blocos | |
| Ni | – | reação normal à base da superfície de deslizamento | |
| Ti | – | força de atrito na superfície de deslizamento | |
| αi | – | inclinação do segmento da superfície de deslizamento | |
| li | – | comprimento do segmento da superfície de deslizamento | |
| φi | – | ângulo de atrito interno do solo no segmento da superfície de deslizamento | |
| ci | – | coesão do solo no segmento da superfície de deslizamento |
Para calcular o equilíbrio de forças e momentos limite através do método de Shahunyants, são consideradas as seguintes premissas:
![]() os planos que divisores dos blocos são sempre verticais
os planos que divisores dos blocos são sempre verticais
![]() a inclinação das forças Ei atuantes entre blocos é zero, as forças atuam horizontalmente
a inclinação das forças Ei atuantes entre blocos é zero, as forças atuam horizontalmente
Método de resolução:
A componente das forças Pyi e Pxi é calculada através das Equações (1) e (2) de forma a obter os valores para as direções das forças Ti e Ni. Para um valor positivo do ângulo αi (como representado no esquema) a força PNi atua na direção oposta a Ni e a força PQi atua na direção oposta a Ti.
![]() (1)
(1)
![]() (2)
(2)
As forças que atuam na direção da superfície de deslizamento relacionam-se de acordo com a seguinte equação:
![]() (3)
(3)
| onde: | Ui | – | empuxo no segmento da superfície de deslizamento |
Equações de equilíbrio para cada bloco:
Equação de equilíbrio na direção normal ao segmento da superfície de deslizamento:
![]() (4)
(4)
Equação de equilíbrio na direção paralela ao segmento da superfície de deslizamento:
![]() (5)
(5)
A partir das Equações (3) e (5) obtém a Equação (6):
![]() (6)
(6)
A partir das Equações (4) e (6) obtém a Equação (7):
![]() (7)
(7)
Desenvolvendo, obtém-se a Equação (8):
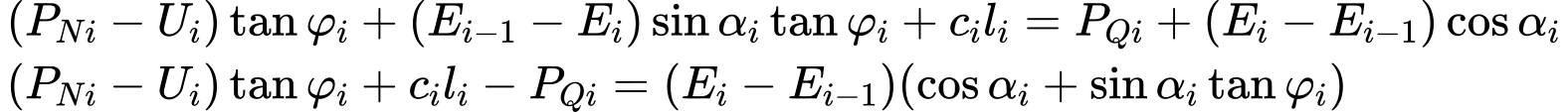 (8)
(8)
Considerando a seguinte equação trigonométrica:
![]() (9)
(9)
E aplicando-a à Equação (8), obtém-se a Equação (10):
![]() (10)
(10)
Que é equivalente a:
![]() (11)
(11)
E pode ser desenvolvida de maneira a obter as foças Ei atuantes entre blocos:
![]() (12)
(12)
Nesta fase, o fator de segurança Ku é introduzido na análise. O fator de segurança consiste no valor que torna o estado das forças que atuam em cada bloco em estados limite. Isto é conseguido através da multiplicação das forças ativas, isto é, as forças que contribuem para o deslizamento do solo acima da superfície de deslizamento, pelo fator de segurança. As forças ativas são consideradas na Equação (12), no termo PQi. Este termo contém tanto as forças ativas com contribuem para o deslizamento do talude como as forças estabilizadoras. As forças desestabilizadoras serão denominadas de PQi,sd, enquanto que as forças estabilizadoras serão denominadas de PQi,ud:
![]() (13)
(13)
Se o valor de PQi for positivo, este contribui para o deslizamento do talude e será considerado como uma força ativa PQi,sd. Se o valor de PQi for negativo, este contribui para o aumento da resistência ao deslizamento e será considerado como uma força PQi,ud. Então, subtraindo o valor de PQi,ud, que é negativo, na Equação (13) significa somar um valor positivo, e a expressão pode ser escrita da seguinte forma:
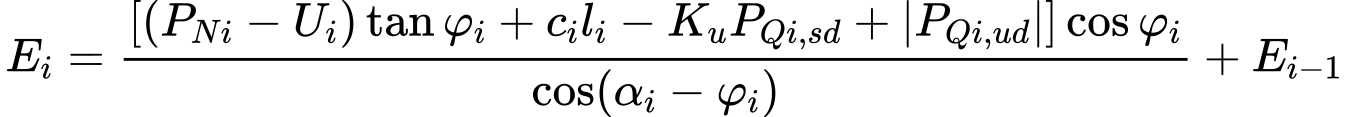 (14)
(14)
Na origem da superfície de deslizamento o valor de E0 = 0. Assim, o valor de E1 é dado por:
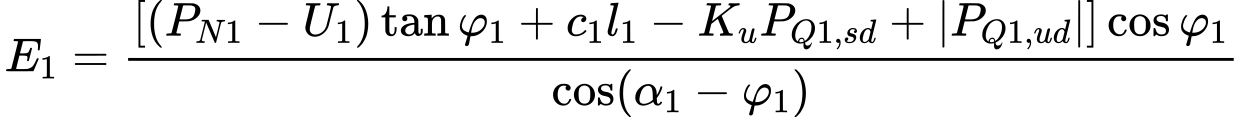 (15)
(15)
O valor de E2 é dado por:
(16)
As restantes forças atuantes entre blocos poderão ser determinadas de forma semelhante. Mantendo a condição de que no ponto final da superfície de deslizamento o valor de En = 0. Desenvolvendo a expressão anterior, obtém-se:
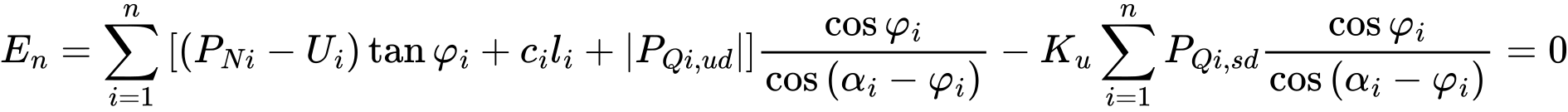 (17)
(17)
Esta expressão pode ser utilizada para a obtenção direta do fator de segurança Ku:
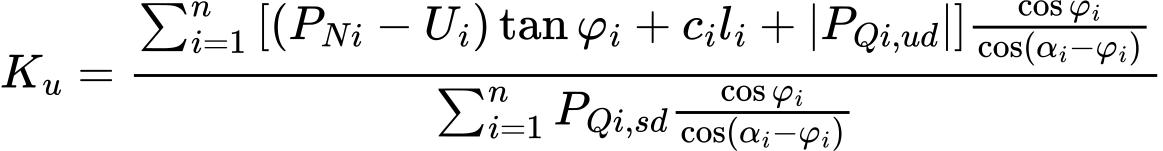 (18)
(18)
Método ITF (Imbalance Thrust Force Method)
O método ITF é um método de verificação dos estados limite. Baseia-se na verificação da equação de equilíbrio das forças atuantes em cada bloco e não considera a equação de equilíbrio de momentos. As premissas consideradas neste método podem ser visualizadas na figura seguinte:
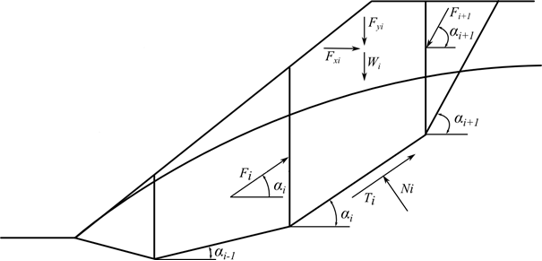 Fig. 1 Esquema das forças atuantes – Método ITF
Fig. 1 Esquema das forças atuantes – Método ITF
Cada bloco estará sujeito às forças seguintes:
| onde: | Wi | – | peso do iésimo bloco, o peso do bloco da parte inferior ao nível freático é determinado considerando o peso volúmico saturado do solo γsat |
| Fyi | – | carga vertical sobrante atuante no bloco | |
| Fxi | – | carga horizontal sobrante atuante no bloco | |
| Fi, Fi+1 | – | forças atuantes entre blocos nas direções dadas pelos ângulos αi e αi+1 |
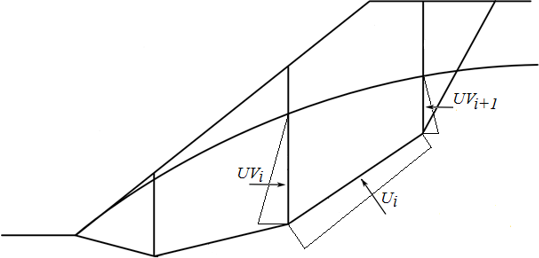 Fig. 2 Esquema do empuxo atuante no bloco
Fig. 2 Esquema do empuxo atuante no bloco
| Ui | – | resultante do empuxo na superfície de deslizamento | |
| UVi,UVi+1 | – | resultante do empuxo nos planos divisores de blocos |
As forças UVi e UVi+1 estão incluídas nas forças horizontais Fxi.
A equação de equilíbrio das forças atuantes na direção normal ao segmento da superfície de deslizamento é dada por:
![]()
As forças atuantes no segmento da superfície de deslizamento relacionam-se conforme a seguinte equação:
![]()
| onde: | φi | – | ângulo de atrito interno do solo |
| ci | – | coesão do solo | |
| li | – | comprimento do segmento da superfície de deslizamento associado ao iésimo bloco |
A equação de equilíbrio de forças na direção do itésimo segmento da superfície de deslizamento (considerando um ângulo αi) permite obter a força Fi atuante entre blocos:
![]()
Introduzindo as Equações (1) e (2) à Equação (3) obtém-se:
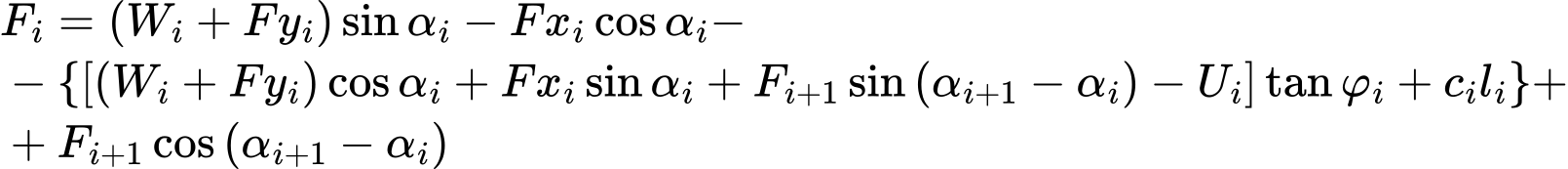
que pode ser desenvolvida de forma a obter a seguinte equação:
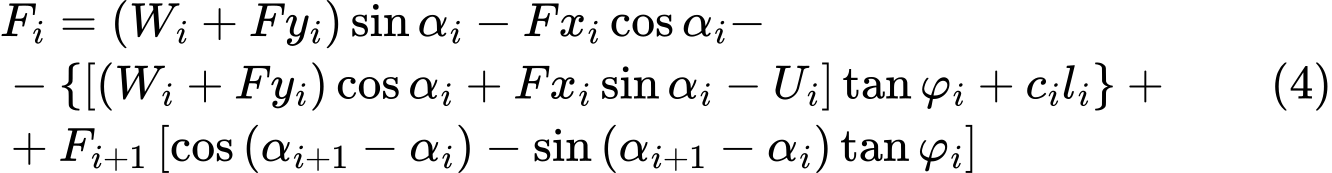
A condição de equilíbrio fica completa com a introdução do fator de segurança FS na análise, dividindo as características do solo c e tanφ por este valor:
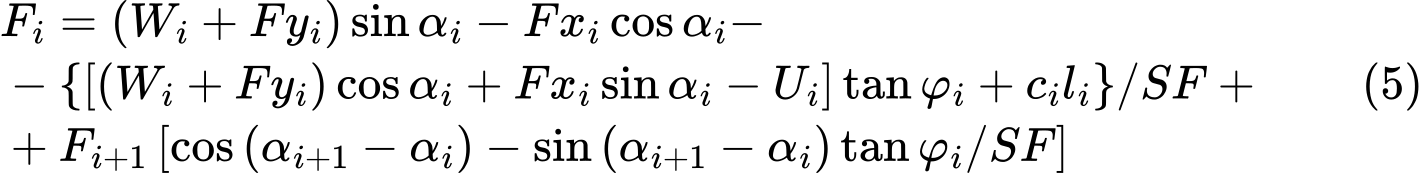
A partir da Equação (5), é possível obter o fator de segurança FS desejado através de um processo iterativo. Este processo desenvolve-se de forma a que a força Fn igual a 0 kN seja aplicada no ponto mais elevado (final) da superfície de deslizamento. As forças Fi atuantes entre blocos são determinadas para um dado fator de segurança FS obtido a partir da Equação (5). Este passo é repetido para vário valores de FS até que se obtenha um valor de FS que permita que a força F0 atuante na base do talude seja igual a 0 kN. Não é assumida nenhuma tensão na superfície de deslizamento. Caso a condição de equilíbrio implique que o valor da força normal Ni seja negativo, o que significa que o solo está carregado à tensão, então o valor desta força é definido como zero na iteração seguinte e a força de cisalhamento Ti atuante num dado segmento é determinada apenas com base na coesão do solo.
O método ITF é muito sensível quanto à forma da superfície de deslizamento. Se a superfície de deslizamento apresentar segmentos com descontinuidades acentuadas, o fator de segurança resultante será mais elevado do que a situação real. Recomenda-se que a diferença na inclinação de segmentos consecutivos da superfície de deslizamento seja inferior a 10°. Isto será verificado automaticamente pelo programa e se esta diferença for superior, o programa emite uma mensagem de aviso a alertar que os resultados poderão estar sobrestimados. Isto não é um problema no caso de superfícies de deslizamento circulares, mas deve ser considerado no caso de superfícies de deslizamento poligonais.
Método ITF – solução explícita
A solução explícita do método ITF apresenta uma forma alternativa para a introdução do fator de segurança na análise. A solução matemática não implica iterações e o fator de segurança resultante é calculado diretamente. Com esta aproximação, o fator de segurança obtido é, normalmente, mais elevado do que a situação real, sendo que esta solução poderá ser desvalorizada, especialmente em casos de superfícies de deslizamento poligonais com grande variância na inclinação entre segmentos consecutivos.
A solução consiste na introdução do fator de segurança FS à Equação (4), de forma a que as componentes ativas das forças sejam multiplicadas por este fator, isto é, as componentes que atuam na direção do deslizamento. Assim, o equilíbrio das forças pode ser escrito da seguinte forma:
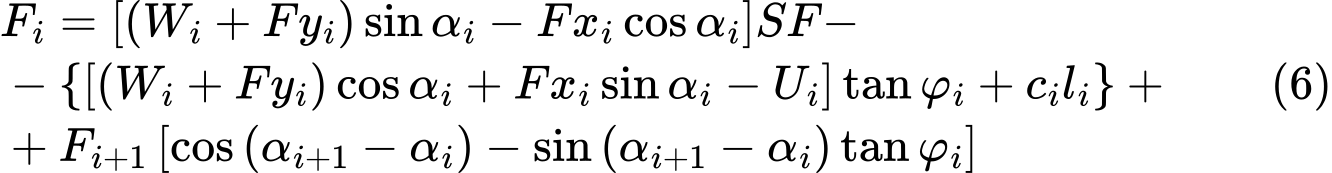
Para clarificar, a componente das forças ativas serão apresentadas como:
![]()
e a componente das forças passivas como:
![]()
e, ainda, a seguinte função auxiliar:
![]()
A Equação (6) pode, então, ser escrita de forma simplificada:
![]()
O próximo passo consiste na introdução da força conhecida Fn=0 de modo a ser possível escrever as seguintes expressões para as forças atuantes entre blocos F:
![]()
![]()
![]()
Etc….
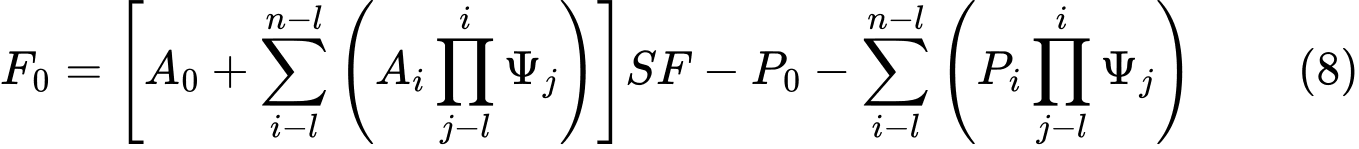
Uma vez que a força atuante no ponto de origem inferior da superfície de deslizamento deve ser igual a 0 kN, obtém-se a expressão final para o cálculo do fator de segurança FS:
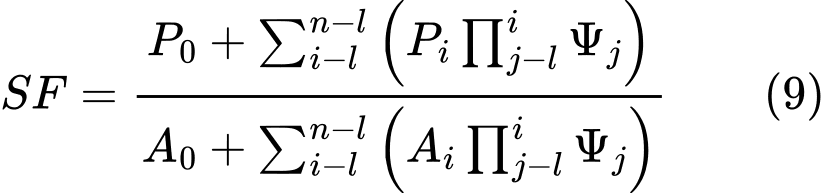
Força de Deslizamento Acrescida
A força de deslizamento acrescida Fn é introduzida como uma força que atua no ponto inferior da superfície de deslizamento – ver figura. Com esta força, o equilíbrio limite pode ser alcançado para o valor do fator de segurança Fsd pretendido e o seu valor pode ser útil para o dimensionamento de um muro de retenção. A força de deslizamento acrescida apresenta um valor razoável se o fator de segurança de dimensionamento for superior ao comum. Quando o fator de segurança comum for elevado o suficiente (a estabilidade do talude é aceitável), o valor da força de deslizamento acrescida é igual a zero.
 Força de deslizamento acrescida Fn
Força de deslizamento acrescida Fn
A força de deslizamento acrescida também pode ser utilizada como critério de otimização. Neste caso, o processo de otimização procura a superfície de deslizamento com o valor máximo para a força de deslizamento acrescida. Este tipo de processo de otimização pode ser utilizado se a estabilidade do taludes para a superfície de deslizamento verificada não for aceitável, porque para uma superfície de deslizamento aceitável, a força de deslizamento acrescida não é calculada (igual a zero). Para a estabilidade de superfícies de deslizamento aceitáveis, o processo de otimização utiliza como critério apenas o fator de estabilidade FS.
Otimização de Superfícies de Deslizamento Poligonais
O processo de otimização de superfície de deslizamento consiste na alteração consecutiva da localização de pontos da superfície de deslizamento, executada automaticamente pelo programa, e na sua verificação, uma vez que a mudança da posição de pontos influencia o valor do fator de segurança da estabilidade do talude FS. Os pontos limite da superfície de deslizamento otimizada são movidos ao longo da superfície do terreno, os pontos da superfície de deslizamento que se distribuem pelo subsolo são movidos nas direções horizontal e vertical. Inicialmente, a distância associada à alteração da localização de um ponto é definida como um décimo da menor distância entre entre dois pontos vizinhos da superfície de deslizamento. A cada nova alteração, esta distância é reduzida para metade. A otimização da superfície de deslizamento baseia-se na alteração da localização dos seus pontos da esquerda para a direita e fica completa quando nenhum ponto se mover.
Durante a otimização da superfície de deslizamento circular, o processo iterativo pode tender para um mínimo local (considerando a evolução gradual da localização dos pontos), podendo ser terminado sem ser encontrada a superfície de deslizamento crítica. No caso de perfis de taludes complexos, é especialmente vantajoso introduzir vários pontos na superfície de deslizamento inicial. A combinação com a aproximação utilizada para as superfícies de deslizamento circulares também é aconselhável. Assim, primeiro é encontrada uma superfície de deslizamento crítica com forma circular que é utilizada para definir a superfície de deslizamento poligonal inicial.
O processo de otimização pode ser limitado devido a diferentes restrições. Isto será um vantagem quando se pretende que a superfície de deslizamento atravesse, ou contorne, um determinada região. As restrições podem ser introduzidas no processo de otimização de duas formas distintas:
- As restrições da otimização podem ser definidas como um conjunto de segmentos do subsolo. Assim, a otimização da superfície de deslizamento será forçada a contornar estes segmentos.
- Outra forma de limitar o processo de otimização é fixar a localização de pontos da superfície de deslizamento otimizada ou permitir o deslocamento destes pontos apenas numa das duas direções possíveis (vertical ou horizontal).
Para o método ITF, a força de deslizamento adicional pode ser utilizada como critério de otimização. Neste caso, o processo de otimização procura a superfície de deslizamento com o máximo valor da força de deslizamento adicional Fn, em vez do fator de estabilidade mínimo FS. Este critério de otimização pode ser aplicado quando a superfície de deslizamento não é aceitável. Para uma superfície de deslizamento aceitável, o processo de otimização utiliza apenas o fator de estabilidade FS.
Alterar a Inclinação dos Planos Divisores
A alteração da inclinação de planos divisores é apenas válida para o método de Sarma. Como mostra a figura a baixo, não é necessário que os planos que dividem os blocos sejam verticais ou paralelos entre eles. Na primeira fase da análise, quando o processo de otimização altera a localização dos pontos da superfície de deslizamento, o programa assume um alinhamento vertical para os planos divisores. Para ser possível obter um valor ainda mais reduzido para a estabilidade do talude, é possível alterar a inclinação dos planos divisores. Este processo é, novamente, realizado em várias fases, com um valor limitado para a alteração da rotação dos planos entre cada fase do processo, que também será reduzido gradualmente ao longo do processo de otimização. Esta fase da otimização termina quando a rotação dos planos for inferior a 1o e não se verifiquem alterações na rotação.
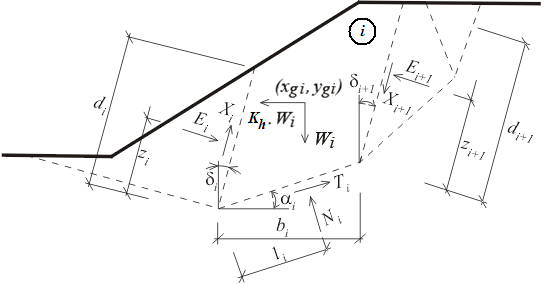 Esquema das forças atuantes – Método de Sarma
Esquema das forças atuantes – Método de Sarma
Superfície de Deslizamento Circular
Para todos os métodos baseados no equilíbrio limite é assumido que o subsolo acima da superfície de deslizamento é dividida em blocos (os planos divisores de blocos são sempre verticais). A figura seguinte mostra as forças atuantes em cada bloco:
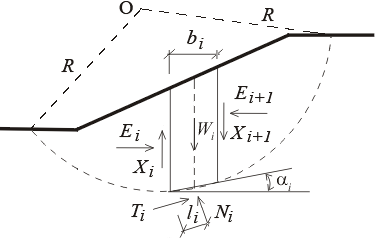 Esquema estático de um bloco
Esquema estático de um bloco
Neste caso, Xi e Ei representam as forças de cisalhamento e normal atuantes entre blocos, Ti e Ni representam as forças de cisalhamento e normal atuantes em cada segmento da superfície de deslizamento, Wi representa o peso de cada bloco.
Os vários métodos baseados na divisão do subsolo acima da superfície de deslizamento em blocos diferem nas premissas para satisfazer as equações de equilíbrio das forças e de momentos em relação ao ponto O.
O programa permite que um dos seguintes métodos seja adotado:
![]() Fellenius / Petterson
Fellenius / Petterson
![]() Bishop
Bishop
![]() Spencer
Spencer
![]() Janbu
Janbu
![]() Morgenstern-Price
Morgenstern-Price
![]() Shahunyants
Shahunyants
![]() Método ITF
Método ITF
A adição do nível freático ao corpo do talude (através de uma das cinco opções possíveis) influencia a análise de duas formas diferentes. Primeiro, ao computar o peso do bloco de solo e segundo, ao determinar as forças de cisalhamento. Tenha em consideração que os parâmetros efetivos do solo são utilizados para relacionar as forças normal e de cisalhamento.
As forças de ancoragem são consideradas como cargas externas aplicadas no talude. Para a análise, considera-se que estas cargas têm um metro de desenvolvimento [kN/m] e são consideradas na equação de equilíbrio de momentos. Estas forças devem contribuir para o aumento da estabilidade do talude, caso isto não seja conseguido de forma diferente. Não existem limitações para a magnitude do valor das forças de ancoragem sendo que se deve trabalhar com valores realistas.
A presença de água acima da superfície do terreno é considerada como um conjunto de forças que atuam perpendicularmente à superfície do terreno, juntamente com o empuxo atuante ao longo da superfície de deslizamento, que depende da profundidade da superfície de deslizamento, medida a partir do nível freático. As forças atuantes na superfície do terreno são consideradas na equação de equilíbrio de momentos, como resultado da multiplicação do valor da força pelo braço em relação ao centro da superfície de deslizamento.
A otimização de superfícies de deslizamento circulares procura a superfície crítica (menor FS).
Fellenius / Petterson
É o método de divisão do subsolo em blocos mais simples, uma vez que considera apenas a equação de equilíbrio global de momentos em relação ao centro da superfície de deslizamento. As forças de cisalhamento e normal atuantes entre blocos Xi e Ei não são consideradas. O fator de segurança FS pode ser obtido diretamente a partir da seguinte expressão:
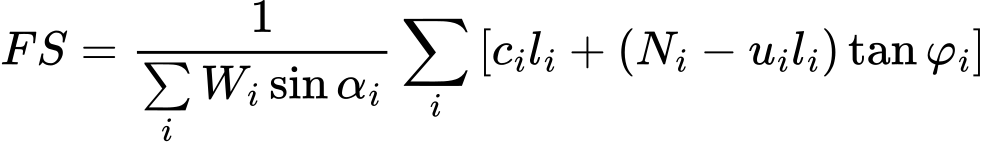
| onde: | ui | – | empuxo atuante no bloco |
| ci,φi | – | valores efetivos dos parâmetros do solo | |
| Wi | – | peso do bloco | |
| Ni | – | força normal atuante no segmento da superfície de deslizamento | |
| αi | – | inclinação do segmento da superfície de deslizamento | |
| li | – | comprimento do segmento da superfície de deslizamento |
Bibliografia:
Petterson KE (1955) The early history of circular sliding surfaces. Geotechnique 5:275-296.
Bishop
O método de Bishop simplificado considera que não existem Xi forças entre blocos. O método baseia-se na verificação da equação de equilíbrio de momentos e a equação de equilíbrio das forças verticais.
O fator de segurança FS pode ser obtido através da iteração da seguinte expressão:
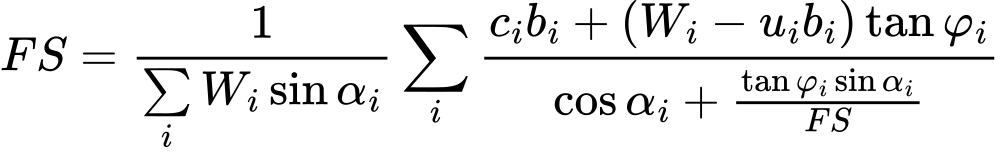
| onde: | ui | – | empuxo atuante no bloco |
| ci,φi | – | valores efetivos dos parâmetros do solo | |
| Wi | – | peso do bloco | |
| αi | – | inclinação do segmento da superfície de deslizamento | |
| bi | – | largura do bloco |
Bibliografia:
Bishop, A.W. (1955) “The Use of the Slip Circle in the Stability Analysis of Slopes”, Geotechnique, Great Britain, Vol. 5, No. 1, Mar., pp. 7-17.
Spencer
Este método considera que não existem forças nulas entre blocos. A resultante das forças normal e de cisalhamento atuantes entre blocos têm inclinações constantes. O método de Spencer é um método rigoroso no que toca à verificação das três equações de equilíbrio – equações de equilíbrio das forças horizontais e verticais e equação de equilíbrio de momentos. O fator de segurança FS é obtido através da iteração da inclinação das forças atuantes entre blocos e do próprio fator de segurança FS. Podem ser encontrados mais detalhes na seção que descreve a análise da superfície de deslizamento poligonal.
Janbu
O método de Janbu assume que não existem forças nulas entre blocos. Este método verifica as equações de equilíbrio das forças horizontais e verticais para todos os blocos e a equação de equilíbrio de momentos para todos os blocos exceto para o último (o superior). Este método requer a escolha da posição das forças atuantes entre blocos. O fator de segurança FS é obtido através da iteração das forças atuantes entre blocos e das inclinações respetivas. Podem ser encontrados mais detalhes na seção que descreve a análise da superfície de deslizamento poligonal.
Morgenstern-Price
Este método considera que não existem forças nulas entre blocos. A resultante das forças normal e de cisalhamento atuantes entre blocos têm inclinações diferentes para cada bloco (forma da função semi-senoidal). O método de Morgenstern-Price é um método rigoroso no que toca à verificação das três equações de equilíbrio – equações de equilíbrio das forças horizontais e verticais e equação de equilíbrio de momentos. O fator de segurança FS é obtido através da iteração da inclinação das forças atuantes entre blocos e do próprio fator de segurança FS. Podem ser encontrados mais detalhes na seção que descreve a análise da superfície de deslizamento poligonal.
Shahunyants
Podem ser encontrados mais detalhes na seção que descreve a análise da superfície de deslizamento poligonal.
Método ITF (Imbalance Thrust Force Method)
Podem ser encontrados mais detalhes na seção que descreve a análise da superfície de deslizamento poligonal.
Otimização da Superfície de Deslizamento Circular
O objetivo do processo de otimização é conseguir uma superfície de deslizamento com o menor fator de segurança de estabilidade de talude FS possível. A superfície de deslizamento circular fica definida através de 3 pontos: dois pontos na superfície do terreno e um ponto no subsolo. Cada ponto à superfície tem um gráu de liberdade, enquanto que o ponto no subsolo tem dois gráus de liberdade. A superfície de deslizamento é caracterizada por quatro parâmetros independentes. A obtenção deste conjunto de parâmetros, para o resultado mais crítico, requer uma análise sensível que resulta numa matriz de mudança de parâmetros que permite um processo de otimização rápido e confiável. A superfície de deslizamento com o menor fator de segurança da estabilidade do talude associado é a superfície de deslizamento crítica. Os parâmetros para cada superfície de deslizamento obtida durante o processo de otimização podem ser visualizados no relatório de resultados.
Esta aproximação é, normalmente, bem sucedida na obtenção da superfície crítica sem incorrer no problema de tender para um mínimo local. Assim, esta aproximação revela-se um bom ponto de partida para a otimização geral de superfícies de deslizamento, como é o caso de superfícies de deslizamento poligonais.
O processo de otimização pode ser limitado devido a diferentes restrições. Isto será um vantagem quando se pretende que a superfície de deslizamento atravesse, ou contorne, um determinada região. As restrições ao processo de otimização podem ser realizadas de duas formas diferentes:
- As restrições da otimização são definidas como um conjunto de segmentos localizados no subsolo. A superfície de deslizamento otimizada é forçada a contornar estes segmentos, durante a otimização.
- Outra forma de restringir o processo de otimização é fixar a localização da extremidade esquerda, ou direita, da superfície de deslizamento otimizada.
Para o método ITF, a força de deslizamento adicional pode ser utilizada como critério de otimização. Neste caso, o processo de otimização procura a superfície de deslizamento com o máximo valor da força de deslizamento adicional Fn, em vez do fator de estabilidade mínimo FS. Este critério de otimização pode ser aplicado quando a superfície de deslizamento não é aceitável. Para uma superfície de deslizamento aceitável, o processo de otimização utiliza apenas o fator de estabilidade FS.
Procura na Grelha
Para superfícies de deslizamento circulares, por vezes, pode ser conveniente exibir várias superfícies de deslizamento em simultâneo. Para tal, selecione a opção “Buscar grelha”.
O cálculo da grelha é sempre realizado com base na superfície de deslizamento definida e, como tal, recomendamos que se realize primeiro a otimização da superfície de deslizamento circular.
Também é possível inserir restrições à superfície de deslizamento.
Na caixa de diálogo, inserimos os parâmetro da grelha (centro, raio, rotação). Após realizar a análise, todas as superfícies de deslizamento ficam calculadas e são exibidas com a escala de cores selecionada.
Configurações dos parâmetros da grelha da superfície de deslizamento
Para uma melhor representação, pode ser, por vezes, mais conveniente considerar o fator de segurança apenas até um determinado nível – isto pode ser definido na caixa de diálogo “Definição da escala de cores” através do botão “Gerar valores“. As superfícies de deslizamento fora do intervalo considerado não são exibidas.
Escala de geração até um determinado nível
Este método também pode ser utilizado como uma otimização manual:
![]() Utilize a superfície de deslizamento definida e realize a análise.
Utilize a superfície de deslizamento definida e realize a análise.
![]() A superfície de deslizamento mais gravosa é exibida a azul e o seu centro fica realçado.
A superfície de deslizamento mais gravosa é exibida a azul e o seu centro fica realçado.
![]() Após voltar a realizar a análise, a superfície de deslizamento mais gravosa é considerada e a grelha é calculada novamente.
Após voltar a realizar a análise, a superfície de deslizamento mais gravosa é considerada e a grelha é calculada novamente.
![]() O processo pode ser repetido até que o centro da superfície de deslizamento final seja o centro da grelha.
O processo pode ser repetido até que o centro da superfície de deslizamento final seja o centro da grelha.
Em todo o caso, este procedimento é menos fiável do que o algoritmo de otimização standard da superfície de deslizamento e recomendamos que seja utilizado com atenção.
Foliação
Pode ser considerada a foliação dos solos. Isto significa que é definido um ângulo de atrito interno e um intervalo para a foliação do solo, quando se definem os parâmetros de um solo <Talude inicial para a foliação; Talude final para a foliação>, o solo passa a apresentar parâmetros (c e φ) muito diferentes (normalmente mais desfavoráveis).
Se a inclinação de um segmento da superfície de deslizamento da interface entre blocos é assumida como pertencente ao intervalo <Talude inicial para a foliação; Talude final para a foliação>, a análise prossegue com os parâmetros c e φ modificados.
Influência de Fendas
O programa permite considerar a influência de fendas que apareçam na superfície do terreno e sejam preenchidas com água h. O único parâmetro a definir é a profundidade das fendas. O efeito destas é considerado quando se calcula as forças normal e de cisalhamento para as secções da superfície de deslizamento que contenham fendas – em secções com fendas os parâmetros da força de cisalhamento são definidos como zero (c = 0, φ = 0). Seguidamente, introduz-se a força horizontal F, devido à presença de água no interior das fendas, na análise (ver figura)
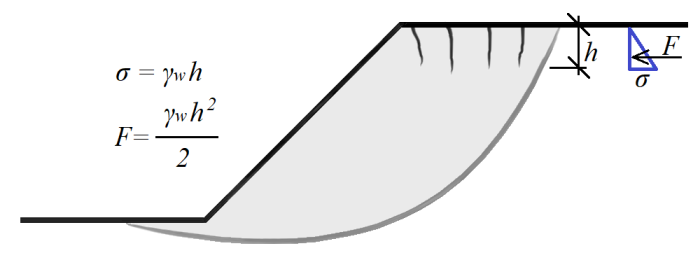 Influência de fendas
Influência de fendas
Estabilidade de Rochas
O programa para analisar a estabilidade de taludes rochosos verifica os seguintes tipos de falhas na superfície de maciços:
![]() Falha de uma superfície de deslizamento plana
Falha de uma superfície de deslizamento plana
![]() Translação de uma superfície de deslizamento poligonal
Translação de uma superfície de deslizamento poligonal
![]() Deslizamento em cunha
Deslizamento em cunha
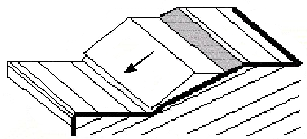 Falha da superfície de uma maciço rochoso devido a uma superfície de deslizamento plana
Falha da superfície de uma maciço rochoso devido a uma superfície de deslizamento plana
 Translação de uma superfície de deslizamento poligonal
Translação de uma superfície de deslizamento poligonal
 Falha em cunha
Falha em cunha
Superfície de Deslizamento Plana
A rotura numa superfície de deslizamento plana é caracterizada pelo deslizamento de um bloco de rocha ao longo da superfície. A cunha da rocha pode ser definida por uma junta de dilatação. O procedimento da análise de estabilidade implica a determinação da força normal N atuante na superfície de deslizamento, a força de cisalhamento Tact (ativa) e a força de cisalhamento resistente Tres (passiva).
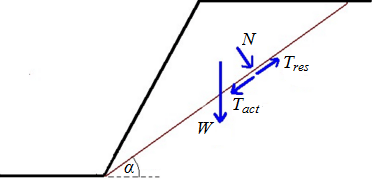 Forças atuantes na superfície de deslizamento
Forças atuantes na superfície de deslizamento
Os parâmetros da resistência ao cisalhamento e a força normal N atuante na superfície de deslizamento são os principais dados a introduzir para a determinação das forças de cisalhamento resistentes Tres. O cálculo da força de cisalhamento ativa Tact e da força normal N é influenciado pelo peso próprio do bloco (depende da geometria e peso volúmico da rocha), ancoragem, sobrecarga, influência do nível freático e efeitos sísmicos. A força ativa Tact e a força normal N são determinadas como o somatório de todas as forças consideradas na análise.
O programa considera diferentes tipos de superfícies de deslizamento:
![]() Suave
Suave
![]() Ondulada
Ondulada
![]() Em degraus
Em degraus
A verificação resultante pode ser realizada de acordo com a metodologia de verificação selecionada na janela “Configurações”.
Superfície de Deslizamento em Degraus
Se o maciço rochoso contiver um sistema de falhas descontinuadas paralelas, inclinadas em relação à superfície do maciço, e um segundo sistema indistinto, é possível considerar a formação de uma superfície de deslizamento em degraus (dentado). Este tipo de superfície pode ser introduzida no programa através da teoria de Calla e Nicholas, que aumenta a resistência da superfície de deslizamento em degraus por Δτ.
![]()
![]()
| onde: | σn | – | tensão normal atuante na direção normal à superfície de deslizamento |
| ν | – | ângulo da ondulação | |
| T | – | resistência à tração efetiva dos degraus da rocha intacta | |
| k | – | parte da altura ht associada aos degraus na rocha intacta (não criados por uma sistema secundário de planos) | |
| ht | – | altura normal da cunha em degraus assente num plano inclinado do sistema principal de planos de descontinuidade | |
| T0 | – | resistência à tração da rocha intacta |
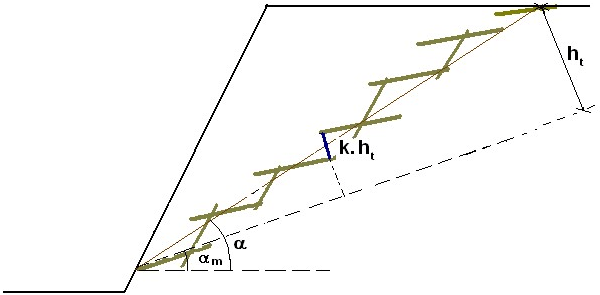 Superfície de deslizamento em degraus
Superfície de deslizamento em degraus
Bibliografia:
W.S. Dershowitz, H.H. Einstein – Characterizing rock joint geometry with joint system models Journal Rock Mechanics and Rock Engineering, Springer Wien ISSN 0723-2632 , Issue Volume 21, Number 1 / January, 1988 Pages 21-51.
Resistência à Tração da Rocha
A resistência à tração Te é 20 a 30x menor que a resistência da rocha à compressão simples σc.
Resistência à tensão simples To para diferentes rochas intactas [MPa]
| Basalto | 3 – 18 |
| Gneisse | 7 – 16 |
| Granito | 11 – 21 |
| Calcário | 3 – 5 |
| Mármore | 7 – 12 |
| Quartzite | 4 – 23 |
| Arenito | 5 – 11 |
| Xisto | 5 – 12 |
| Ardósia | 2 – 17 |
| Tufo | 2 – 4 |
Superfície de Deslizamento Ondulada
Se for considerada uma superfície de deslizamento ondulada (numa escala de 1 a 10 m) – é possível considerar uma ondulação da superfície de deslizamento através do ângulo ν:
![]()
| onde: | α | – | ângulo da superfície de deslizamento |
| αi | – | ângulo da i-ésima falha da superfície de deslizamento |
A ondulação aumenta a resistência à tração τ na superfície de deslizamento em Δτ:
![]()
| onde: | σn | – | tensão normal atuante na direção normal da superfície de deslizamento |
| ν | – | ângulo da ondulação |
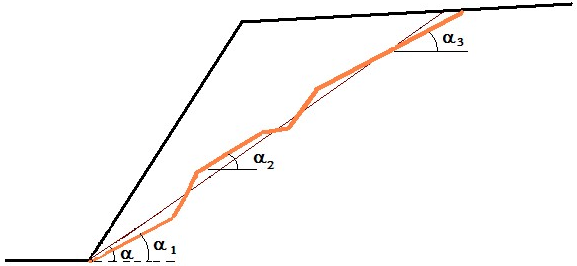 Superfície de deslizamento ondulada
Superfície de deslizamento ondulada
Bibliografia:
Miller, S.M. (1988). Modeling Shear Strength at Low Normal Stresses for Enhanced Rock Slope Engineering, Proc. Of 39th Highway Geology Symp, 346-356.
Ancoragem do Talude Rochoso
Podem ser definidos dois tipos de ancoragem ao realizar a análise de estabilidade do talude, numa superfície de deslizamento plana:
Ativa
Uma ancoragem ativa consiste numa ancoragem pré-esforçada, para a qual as forças de ancoragem são ativadas antes do deslizamento do bloco de rocha. A força normal aumenta a tensão normal na superfície de deslizamento assim como as forças resistentes; a componente tangente da força normal é adicionada ou subtraída das forças de cisalhamento (ativas).
Passiva
Uma ancoragem passiva é ativada pelo deslizamento de um bloco de rocha (isto é, não são ancoragens pré-tensionadas). As forças normais aumentam a tensão normal na superfície de deslizamento, assim como as forças resistentes; a componente tangente da força normal é adicionada às forças resistentes.
 Força de ancoragem
Força de ancoragem
Sobrecarga no Talude Rochoso
A sobrecarga é determinada em primeiro lugar. A componente normal da força resultante aumente a tensão normal na superfície de deslizamento, assim como as forças resistentes Tres.. A componente tangente é adicionada ou subtraída às forças de cisalhamento (ativas) Tact.
 Sobrecarga
Sobrecarga
Influência do Nível Freático na Superfície de Deslizamento
Estão disponíveis as seguintes opções para considerar o nível freático:
| Sem nível freático, nível freático não é considerado | |
| Pressão hidrostática, nível freático acima da base do talude | |
| Pressão hidrostática, nível freático na junta de dilatação | |
| Pressão hidrostática, nível freático na junta de dilatação, máximo | |
| Pressão hidrostática, nível freático atuante apenas na junta de dilatação | |
| Valor definido para a força do nível freático atuante na superfície de deslizamento | |
| Comportamento definido para a força do nível freático |
Nível Freático acima da Base do Talude
| Pressão hidrostática, nível freático acima da base do talude |
A superfície de deslizamento está completamente ou parcialmente abaixo do nível freático (a água não pode atravessar a superfície de deslizamento), a pressão hidrostática máxima está na base da superfície de deslizamento.
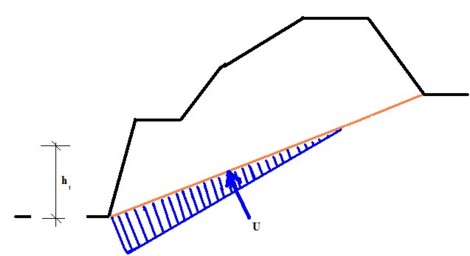 Pressão hidrostática na superfície de deslizamento
Pressão hidrostática na superfície de deslizamento
O valor da pressão hidrostática u na base do talude é dado por:
![]()
| onde: | γw | – | peso volúmico da água |
| ht | – | altura do nível freático acima da base do talude |
A força de compressão da água resultante, atuante na direção normal da superfície de deslizamento, é dada por:
![]()
| onde: | γw | – | peso volúmico da água |
| ht | – | altura do nível freático acima da base do talude | |
| α | – | inclinação da superfície de deslizamento em relação à horizontal |
Nível Freático na Junta de Dilatação
| Pressão hidrostática, nível freático na junta de dilatação |
A superfície de deslizamento está completamente abaixo do nível freático; o nível freático interseta a junta de dilatação ou está alinhada com a superfície do terreno. O valor máximo da pressão hidrostática encontra-se na base do talude.
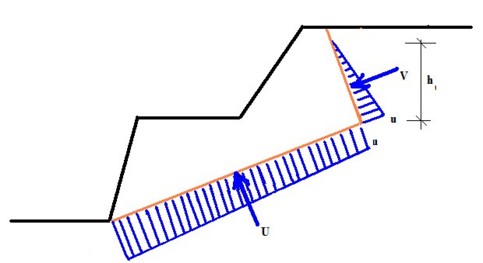 Pressão hidrostática na superfície de deslizamento e junta de dilatação, valor máximo na base do talude
Pressão hidrostática na superfície de deslizamento e junta de dilatação, valor máximo na base do talude
O valor da pressão hidrostática u na intersecção da superfície de deslizamento e a junta de dilatação é dado por:
![]()
| onde: | γw | – | peso volúmico da água |
| ht | – | altura do nível freático acima da linha de interseção da superfície de deslizamento e da junta de dilatação |
A força de compressão da água resultante V, atuante na direção normal da junta de dilatação, é dada por:
![]()
| onde: | γw | – | peso volúmico da água |
| ht | – | altura do nível freático acima da linha de interseção da superfície de deslizamento e da junta de dilatação | |
| φ | – | inclinação da junta de dilatação em relação à vertical |
O valor da pressão hidrostática u1 na base do talude, é dado por:
![]()
| onde: | γw | – | peso volúmico da água |
| Hw | – | altura do nível freático acima da base do talude |
A força de compressão da água resultante U, atuante na direção normal da junta de dilatação, é dada por:
![]()
| onde: | u | – | pressão hidrostática na linha de interseção da superfície de deslizamento e da junta de dilatação |
| u1 | – | pressão hidrostática na base do talude | |
| ht | – | altura do nível freático acima da linha de interseção da superfície de deslizamento e da junta de dilatação | |
| α | – | inclinação da superfície de deslizamento em relação à horizontal | |
| Hw | – | altura do nível freático acima da base do talude |
Nível Freático atuante Apenas na Junta de Dilatação
| Pressão hidrostática, nível freático atuante apenas na junta de dilatação |
A superfície de deslizamento está totalmente seca (não são possíveis infiltrações). O nível freático interseta a junta de dilatação ou está alinhado com o terreno. O valor máximo do impulso hidrostático encontra-se na interseção da superfície de deslizamento e da junta de dilatação.
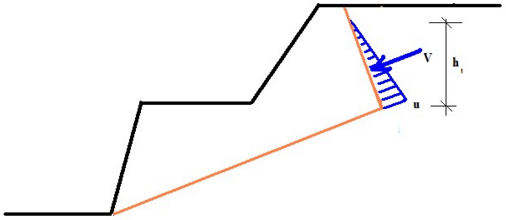 Nível freático atuante na junta de dilatação
Nível freático atuante na junta de dilatação
O valor da pressão hidrostática u na intersecção da superfície de deslizamento e a junta de dilatação é dado por:
![]()
| onde: | γw | – | peso volúmico da água |
| ht | – | altura do nível freático acima da linha de interseção da superfície de deslizamento e da junta de dilatação |
A força de compressão da água resultante V, atuante na direção normal da junta de dilatação, é dada por:
![]()
| onde: | γw | – | peso volúmico da água |
| ht | – | altura do nível freático acima da linha de interseção da superfície de deslizamento e da junta de dilatação | |
| φ | – | inclinação da junta de dilatação em relação à vertical |
O valor da pressão hidrostática atuante na superfície de deslizamento é igual a zero
Valor Definido para a Força do Nível Freático atuante na Superfície de Deslizamento
| Valor definido para a força do nível freático atuante na superfície de deslizamento |
O programa permite a introdução manual de um valor constante para pressão hidrostática ps [kPa] atuante na superfície de deslizamento.
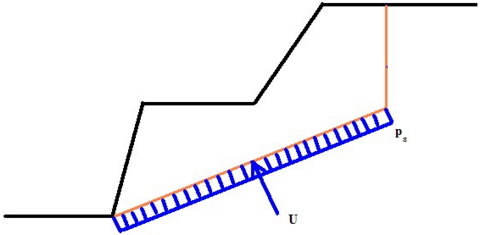 Valor definido para a pressão hidrostática na superfície de deslizamento
Valor definido para a pressão hidrostática na superfície de deslizamento
Comportamento Definido para a Força do Nível Freático
| Comportamento definido para a força do nível freático |
O programa permite a introdução manual de um valor constante para pressão hidrostática pt [kPa] atuante na superfície de deslizamento e pt [kPa] atuante na junta de dilatação.
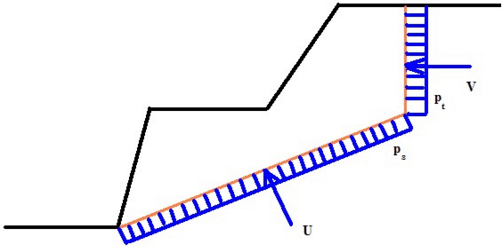 Valores definidos para a pressão hidrostática na superfície de deslizamento e junta de dilatação
Valores definidos para a pressão hidrostática na superfície de deslizamento e junta de dilatação
Superfície de Deslizamento Poligonal
O programa executa a análise de estabilidade de blocos de rocha que se movem ao longo de uma superfície de deslizamento poligonal. Dada a complexidade do método de análise geral, o programa admite as seguintes suposições: Superfície de deslizamento poligonal
Superfície de deslizamento poligonal
Geometria do Bloco de Rocha
A geometria do bloco é determinada pela inclinação α, pelo comprimento de uma dada superfície de deslizamento l e pela inclinação de uma junta divisória φ que separa o bloco subsequente, assim como a inclinação α e o comprimento l da face superior da superfície externa do talude rochoso (perfil natural). Os comprimentos dos planos podem ser definidos pelo comprimento total ou pelos comprimentos das suas projeções vertical e horizontal. É necessário assegurar a condição de que todos os blocos de rocha estão em contacto (a abertura entre juntas não é permitida).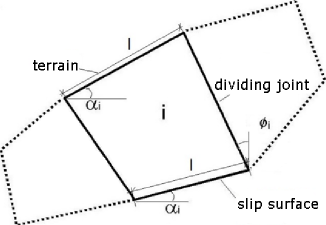 Geometria do iésimo elemento
Geometria do iésimo elemento
Forças de Ancoragem, Sobrecarga
É possível introduzir forças de ancoragem e sobrecargas nos blocos de rocha. As forças resultantes Pi [kN/m] atuantes no iésimo bloco são determinadas posteriormente. Todas as forças atuantes nos blocos, incluindo a pressão hidrostática na superfície de deslizamento e nas juntas que separam os blocos, são consideradas.Sobrecargas atuantes no bloco
É possível introduzir sobrecargas superficiais, contínuas e trapezoidais. O programa determina o seu efeito em cada bloco de rocha.Forças de ancoragem
A força de ancoragem aplicada é considerada para 1 m de profundidade, com base no espaçamento horizontal entre ancoragens especificado.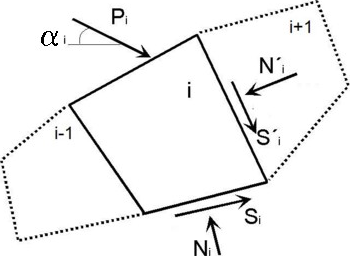 Forças externas atuantes no iésimo elemento
Forças externas atuantes no iésimo elemento
Influência do Nível Freático
A influência do nível freático pode ser considerada através das seguintes opções: nível freático com forma geral, nível freático horizontal ou com o nível freático a atuar diretamente nos blocos.Nível freático com forma geral
A forma geral do nível freático é introduzida como um polígono. A pressão nos poros (tensão) na superfície de deslizamento é considerada linear, de acordo com a seguinte equação: u = γw * zw.| onde: | γw | – | peso volúmico da água |
| zw | – | altura do nível freático nas juntas acima da superfície de deslizamento |
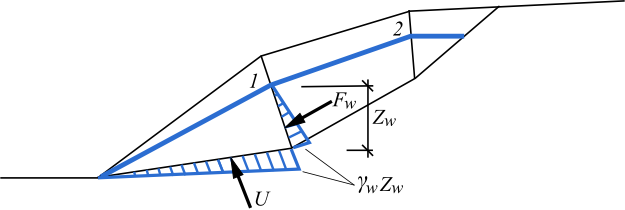 Forças devido ao nível freático atuante no bloco – a água pode escoar livremente através da junta
Forças devido ao nível freático atuante no bloco – a água pode escoar livremente através da junta
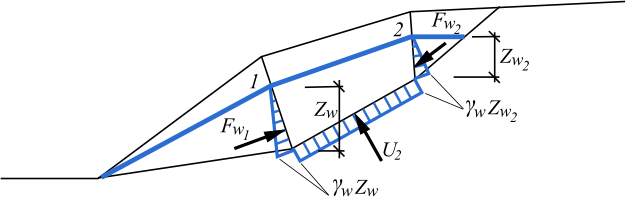 Forças devido ao nível freático atuante no bloco – a água não pode escoar através da junta
Forças devido ao nível freático atuante no bloco – a água não pode escoar através da junta
Nível freático horizontal
O nível freático horizontal é introduzido através de uma altura constante hw acima da base do talude (a partir da origem do sistema de coordenadas). A pressão hidrostática é considerada a partir da cota do nível freático até ao ponto em análise, medida na vertical.Nível freático atuante diretamente nos blocos
A pressão hidrostática ao longo das juntas e da superfície de deslizamento pode ser considerada. Esta é introduzida como uma carga externa:Força devido ao nível freático na superfície de deslizamento interna (água entre blocos) Fv
Deve ser introduzida na análise sempre que for expectável a presença de água nas juntas entre os blocos. É aplicada como uma força resultante Fv em kN (é considerada a pressão atuante na parte submersa da junta por 1m de desenvolvimento).Força devido ao nível freático na superfície de deslizamento externa (impulso hidrostático) U
É definido como uma pressão hidrostática em cada superfície de deslizamento do polígono (superfície de deslizamento externa) separadamente e introduzida como uma carga externa (impulso hidrostático) U em kN, que pode ser reduzido dependendo da permeabilidade da superfície de deslizamento (é considerada a pressão atuante na parte submersa da superfície de deslizamento por 1m de desenvolvimento).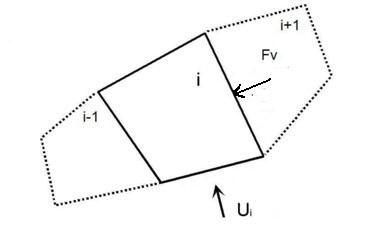 Forças devido ao nível freático atuante no bloco
Forças devido ao nível freático atuante no bloco
Procedimento de Análise
O princípio do cálculo da estabilidade de um talude rochoso para uma superfície de deslizamento poligonal é demonstrado na figura seguinte.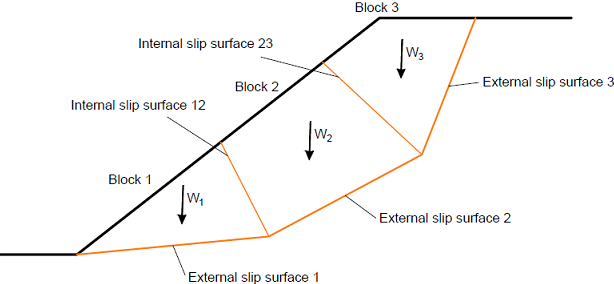 Esboço do talude rochoso
Esboço do talude rochoso
![]()
| onde: | Wi | – | peso do bloco |
| Pi | – | forças externas (cargas) atuantes no bloco | |
| Ei | – | forças sísmicas atuantes no bloco | |
| Ui | – | força devido à água na superfície de deslizamento externa | |
| Vi | – | força devido à água na superfície de deslizamento interna | |
| Hi | – | força devido à água acima da superfície | |
| Bi | – | força de ancoragem no bloco |
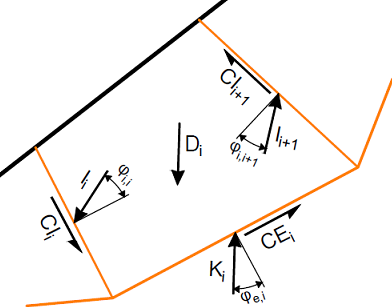 Forças atuantes no bloco
Forças atuantes no bloco
| onde: | D | – | resultante de todas as forças externas atuantes no bloco |
| CI | – | coesão na superfície de deslizamento interna | |
| CE | – | coesão na superfície de deslizamento externa | |
| I | – | força de interação | |
| K | – | força de reação na superfície de deslizamento externa |
![]()
![]()
![]()
| onde: | Ti | – | força resistente |
| φi | – | ângulo de atrito interno na superfície de deslizamento interna | |
| RN,i | – | componente normal de R | |
| RT,i | – | componente tangencial de R | |
| CIi | – | coesão na superfície de deslizamento interna |
![]()
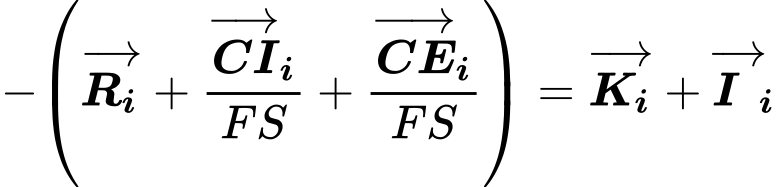
Conceito do Cone de Atrito
O conceito do cone de atrito é a combinação do método cinemático e cinético, utilizado para encontrar a superfície de deslizamento de rotura potencial. O princípio da análise é demonstrado na figura seguinte.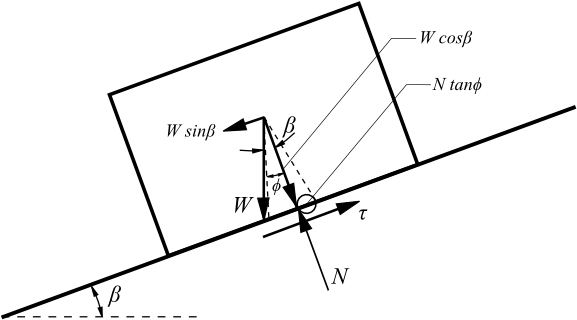 Conceito do cone de atrito para um bloco assente num plano inclinado (superfície de deslizamento poligonal)
Conceito do cone de atrito para um bloco assente num plano inclinado (superfície de deslizamento poligonal)
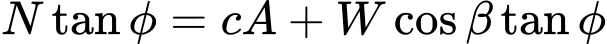
Cunha de Rocha
O programa executa a análise de estabilidade de uma cunha de rocha localizada entre duas superfícies (planos) e que desliza na direção da linha de interseção destes dois planos. A cunha de rocha pode ser definida através de uma junta de dilatação. A inclinação desta interseção deve ser consideravelmente superior ao ângulo de atrito interno dos planos divisores, onde a linha de queda de ambos os planos divisores deve estar direcionada para a linha de interseção. Assume-se que a linha de interseção se localiza num maciço rochoso estável. A solução requer a determinação da força normal N, da força de cisalhamento Tact (ativa) e da força de cisalhamento resistente (passiva) Tres, atuantes nas superfícies de deslizamento A1 e A2. A força ativa Tact e a força normal N consistem no somatório de todas as foças consideradas na análise, após realizar a distribuição destas forças. Os parâmetros de resistência ao cisalhamento de Mohr-Coulomb e a força normal N atuante na superfície de deslizamento são os principais dados a introduzir para a determinação das forças de cisalhamento resistentes Tres. O cálculo da força de cisalhamento ativa Tact e da força normal N é influenciado pelo peso da cunha, (depende da geometria da cunha e do peso volúmico da rocha), ancoragem da cunha, sobrecarga atuante na cunha, influência do nível freático e efeitos sísmicos. A verificação é executada consoante a metodologia de verificação selecionada na janela “Configurações”.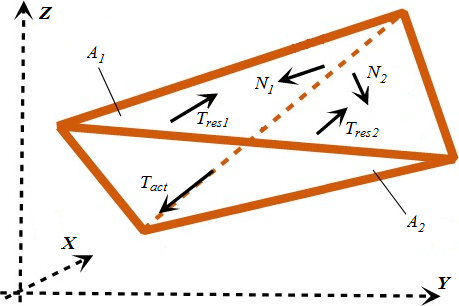 Forças atuantes numa cunha de rocha
Forças atuantes numa cunha de rocha
Geometria da Cunha de Rocha
A definição da geometria da cunha de rocha através da sua inclinação ou da direção da linha de queda, implica a definição da orientação espacial da superfície da rocha, terreno (superfície), superfícies de deslizamento N1 e N2 e/ou junta de dilatação, de modo a que: a) Superfície de rocha pendente b) Superfície de rocha suspensa
a) Superfície de rocha pendente b) Superfície de rocha suspensa
 Descrição da orientação das superfícies – inclinação e direção
Descrição da orientação das superfícies – inclinação e direção
Projeção Estereográfica
Ao definir a geometria da cunha e superfícies de deslizamento, o programa exibe cada superfície através da projeção hemisférica dos círculos de Lambert. Princípio da projeção estereográfica (Projeção de Lambert)
Princípio da projeção estereográfica (Projeção de Lambert)
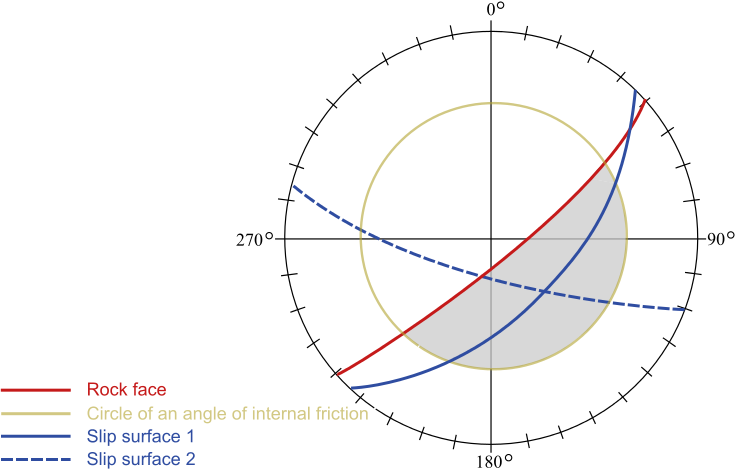 Possibilidade cinemática da cunha de rocha (Ensaio de Markland numa projeção estereográfica)
Possibilidade cinemática da cunha de rocha (Ensaio de Markland numa projeção estereográfica)
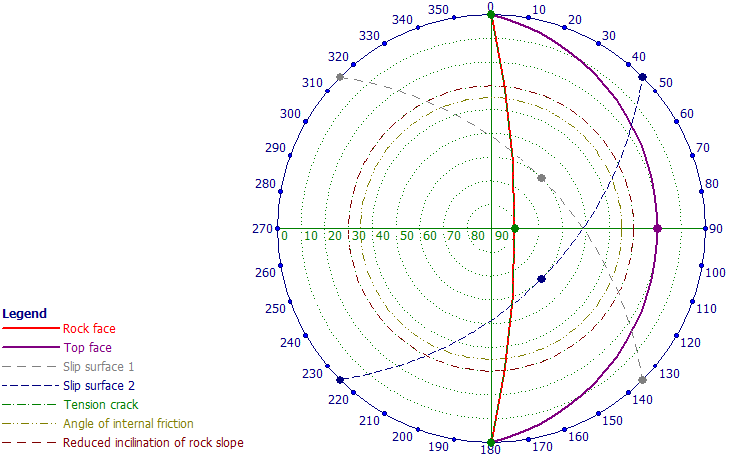 Ensaio de Markland
Ensaio de Markland
Influência do Nível Freático
Por defeito, o programa executa a análise de estabilidade de uma cunha de rocha sem considerar o nível freático. Caso se pretenda considerar o nível freático, é necessário introduzir a altura respetiva, medida a partir da linha de interseção das superfícies de deslizamento com a superfície da rocha (o nível freático pode assumir uma qualquer posição acima da cunha de rocha). O programa assuem que a água pode fluir livremente por entre as descontinuidades abaixo do nível freático (não são consideradas restrições, ex.: blocos de gelo). A pressão hidrostática atua na direção normal às superfícies de deslizamento, contra as componentes normais das forças passivas. Se a altura yw acima do ponto de pressão máxima Pmax for maior ou igual a Z/2 e estiver totalmente contido na cunha de rocha, então o seu valor é assumido como igual a Z/2 (caso A). Se a altura yw acima do ponte de pressão máxima Pmax for inferior a Z/2 (caso B), então o seu valor é reduzido: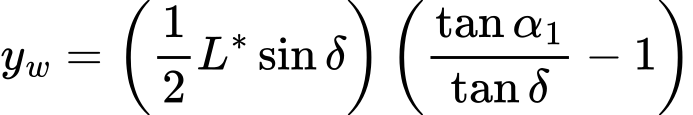
| onde: | L* | – | comprimento da linha de interseção das superfícies de deslizamento A1, A2 |
| α1 | – | inclinação da superfície da rocha | |
| δ | – | inclinação da linha de interseção das superfícies de deslizamento |
![]()
![]()
| onde: | Z | – | altura do nível freático acima da linha de interseção das superfícies de deslizamento e a superfície da rocha |
| Pmax | – | pressão hidrostática máxima na linha de interseção das superfícies de deslizamento | |
| γw | – | peso volúmico da água (≈ 10 kN/m3) | |
| A1w | – | área da parte molhada da superfície de deslizamento 1 | |
| A2w | – | área da parte molhada da superfície de deslizamento 2 |
 Distribuição da pressão hidrostática na linha de interseção das superfícies de deslizamento
Distribuição da pressão hidrostática na linha de interseção das superfícies de deslizamento
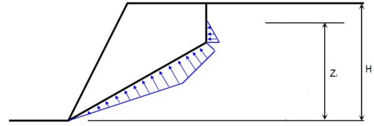 Distribuição da pressão hidrostática ao considerar o nível freático na junta de dilatação
Distribuição da pressão hidrostática ao considerar o nível freático na junta de dilatação
Forças Atuantes
As forças atuantes na cunha de rocha (peso da cunha de rocha, carga externa, força de ancoragem) são decompostas nas direções normais aos planos A1 e A2 (a cunha do bloco está entre estas superfícies) e na direção da sua intersecção. A decomposição das forças resulta nas forças normais N1, N2 atuantes nos planos A1 e A2 e nas forças resistentes (passivas) Tres1, Tres2 atuantes ao longo dos planos A1 e A2. O passo seguinte é a computação da força de cisalhamento (ativa) Tact atuante na direção da linha de interseção das superfícies de deslizamento. A força de cisalhamento (ativa) Tact resultante é obtida através do somatório das forças de cisalhamento individuais Tact,i. A força resistente (passiva) Tres é determinada através da soma das componentes Tres1, Tres2 (ex.: devido a cargas externas) e das forças de atrito nos planos A1 e A2 devido às forças normais.to normal forces:![]()
| onde: | c1 | – | coesão na superfície de deslizamento A1 |
| c2 | – | coesão na superfície de deslizamento A2 | |
| φ1 | – | ângulo de atrito interno na superfície de deslizamento A1 | |
| φ2 | – | ângulo de atrito interno na superfície de deslizamento A2 | |
| Tres1 | – | forças resistentes na superfície de deslizamento A1 | |
| Tres2 | – | forças resistentes na superfície de deslizamento A2 |
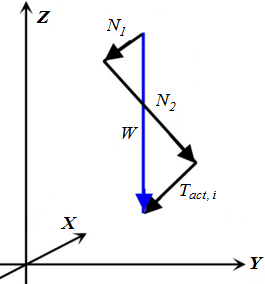 Decomposição do peso próprio da cunha de rocha W
Decomposição do peso próprio da cunha de rocha W
Verificação
A verificação pode ser executada de acordo com a metodologia de verificação selecionada na janela “Configurações”.Verificação de acordo com o Fator de Segurança
Ao executar a verificação de acordo com o fator de segurança, o programa determina diretamente o valor do fator de segurança FS. A condição da verificação assume a seguinte forma:![]()
| onde: | Tact | – | forças de cisalhamento ao longo da superfície de deslizamento |
| Tres | – | forças passivas ao longo da superfície de deslizamento | |
| SF | – | fator de segurança | |
| SFs | – | fator de segurança imposto (a inserir na secção “Análise de estabilidade”) |
Verificação de acordo com a Teoria dos Estados Limite
Ao executar a verificação de segurança de acordo com a teoria dos estados limite, o programa reduz os parâmetros materiais da rocha (ângulo de atrito interno ou tangente do ângulo de atrito interno, coesão) atrevés de coeficientes parciais introduzidos na secção “Análise de estabilidade”. A condição de verificação é a seguinte:![]()
| onde: | Tact | – | forças de cisalhamento (ativas) ao longo da superfície de deslizamento |
| Tres | – | forças passivas ao longo da superfície de deslizamento | |
| γs | – | coeficiente de redução da estabilidade global da construção (inserir em “Análise de estabilidade”) |
Ao análisar uma superfície de deslizamento poligonal, o programa compara o valor calculado com o valor correspondente ao de dimensionamento sob tensão total (o estado de equilíbrio sem reservas). A condição de verificação é a seguinte:
![]()
| onde: | SF | – | fator de segurança calculado com os parâmetros materiais reduzidos |
| SFs | – | coeficiente da estabilidade global da estrutura |
Rocha – Critério de Resistência ao Cisalhamento
A resistência ao cisalhamento é o critério básico para a determinação das forças resistentes passivas. A força resistente é dada pela seguinte expressão:
![]()
| onde: | τ | – | resistência ao cisalhamento na superfície de deslizamento |
| l | – | comprimento da superfície de deslizamento |
A resistência ao cisalhamento para uma superfície de deslizamento plana pode ser dada por:
![]() Mohr – Coulomb
Mohr – Coulomb
![]() Hoek – Brown
Hoek – Brown
![]() Barton – Bandis
Barton – Bandis
Mohr – Coulomb
A resistência ao cisalhamento τ [kPa], segundo Mohr-Coulomb, é dada por:
![]()
| onde: | N | – | força normal atuante na superfície de deslizamento |
| l | – | comprimento da superfície de deslizamento | |
| c | – | coesão da rocha na superfície de deslizamento | |
| φ | – | ângulo de atrito interno na superfície de deslizamento |
Os intervalos aproximados para os parâmetros de rotura de Mohr-Coulomb, para diferentes solos, podem ser encontrados aqui.
Parâmetros de Mohr – Coulomb
Caso seja possível, os parâmetros de resistência devem ser determinados através de ensaios de campo. Os resultados dos ensaios de campo e laboratoriais mostram que o ângulo de atrito interno, para a maior parte das descontinuidades em maciços rochosos, se encontra dentro do intervalo 27° a 47°. Os valores aproximados para o ângulo de atrito interno φ e coesão c de rochas, com base na classificação RMR, estão resumidos na tabela seguinte:
| Classe da rocha | I | II | III | IV | V |
| RMR | 100 – 81 | 80 – 61 | 60 – 41 | 40 – 21 | < 20 |
| Ângulo de atrito interno φ [°] | > 45 | 35 – 45 | 25 – 45 | 15 – 25 | < 15 |
| Coesão c [kPa] | > 400 | 300- 400 | 200 – 300 | 100 – 200 | < 100 |
Hoek – Brown
O critério de rotura de Hoek-Brown descreve a rotura de um maciço rochoso (com base em centenas de análises realizadas em estruturas subterrâneas e taludes rochosos) como::
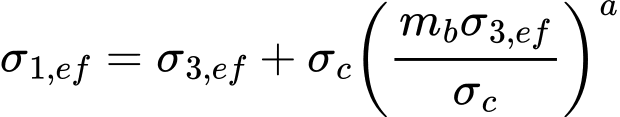
| onde: | σ1ef | – | tensão principal máxima durante a rotura da rocha |
| σ3ef | – | tensão principal mínima durante a rotura da rocha | |
| σc | – | resistência da rocha intacta à compressão simples | |
| σci | – | resistência da rocha intacta à compressão uniaxial | |
| mb,s | – | constante não linear do material, dependente da qualidade da rocha | |
| a | – | coeficiente de dependência da rotura da rocha |
Os parâmetros básicos do modelo modificado de Hoek-Brown devem ser determinados a partir de ensaios de campo e laboratoriais. Para ficar mais familiarizado com este modelo, é fornecida uma breve lista de intervalos de parâmetros individuais. Se a classificação do maciço rochoso através de GSI for conhecida, então é possível que o programa determine os parâmetros H-B automaticamente.
Para a análise em curso, os parâmetros H-B são transformados em parâmetros M-C. A metodologia da análise torna-se idêntica à de Mohr-Coulomb.
Para a conversão dor parâmetros de Hoek-Brown, é utilizada a metodologia de Hoek, Carranza-Torres e Corkum (2002), na análise da estabilidade de taludes rochosos:
Ângulo de atrito interno φ:
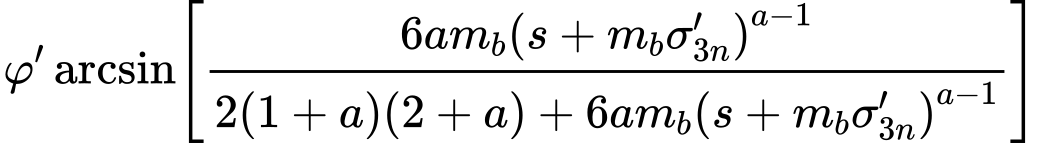
Coesão (resistência ao cisalhamento) c:
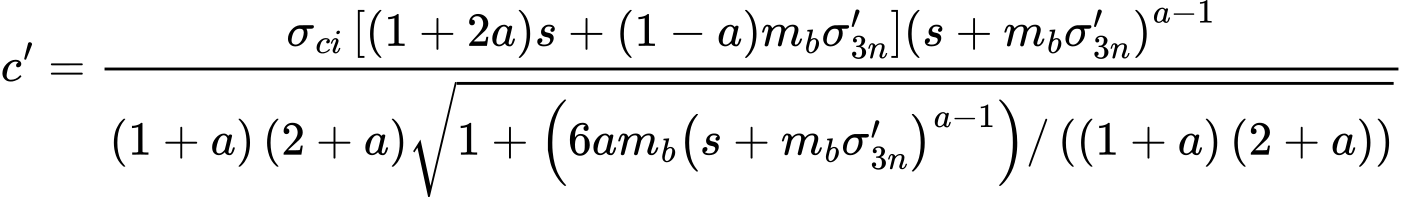
onde:
![]()
O valor máximo de uma tensão principal menor σ‘3max é dado por:
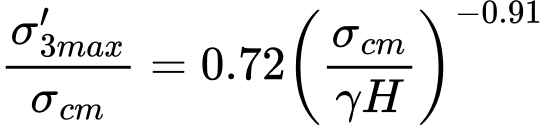
| onde: | γ | – | peso volúmico da rocha |
| H | – | altura do talude rochoso | |
| σc | – | resistência da rocha intacta à compressão simples ou resistência do maciço rochoso intacto à compressão uniaxial |
Bibliografia:
Stability analysis of rock slopes with a modified Hoek-Brown failure criterion, ANG Xiao-Li ; LIANG LI ; YIN Jian-Hua International journal for numerical and analytical methods in geomechanics. ISSN 0363-9061, 2004, vol. 28, no2, pp. 181-190.
Hoek E, Carranza-Torres CT, Corkum B.: Hoek–Brown failure criterion—2002 edition. Proceedings of the 5th North American Rock Mechanics Symposium, Toronto, Canada, vol. 1, 2002, pp. 267 – 273.
Parâmetros de Hoek – Brown
Parâmetros de rotura da rocha a
O parâmetro é um expoente que assume os valores de 0.5 até 0.65 (para a condição original de Hoek-Brown é igual a 0.5) e depende do gráu de rotura da rocha.
Parâmetros não lineares mb = m, s para a = 0.5
(o índice r simboliza valores residuais)
| Rochas de carbonato com clivagem bem desenvolvida – dolomita, pedra calcária, mármore | Rochas argilosas – barro, silte, xisto, ardósia | Rochas arenosas – arenito, quartzito | Rochas cristalinas ígneas de graduação fina – andesita, dolerite, basalto, riólito | Rochas metamórficas e ígneas grosseiras – gabro, gneis, granito | |
Material de rocha intacta, Amostras laboratoriais sem descontinuidades, RMR = 100, Q = 500 | m = 7.00
s = 1.00
mr = 7.00
sr = 1.00 | m = 10.00
s = 1.00
mr = 10.00
sr = 1.00 | m = 15.00
s = 1.00
mr = 15.00
s = 1.00 | m = 17.00
s = 1.00
mr = 17.00
s = 1.00 | m = 25.00
s = 1.00
mr = 25.00
s = 1.00 |
Rocha com muito boa qualidade, Rochas sem blocos isolados com descontinuidades não expostas, RMR = 85, Q = 100 | m = 2.40
s = 0.082
mr = 4.10
sr = 0.189 | m = 3.43
s = 0.082
mr = 5.85
sr = 0.189 | m = 5.14
s = 0.082
mr = 8.78
sr = 0.189 | m = 5.82
s = 0.082
mr = 9.95
sr = 0.189 | m = 8.56
s = 0.082
mr = 14.63
sr = 0.189 |
Rocha de boa qualidade, Rochas ligeiramente danificadas com descontinuidades não expostas e espaçamento de 1 a 3 m, RMR = 65, Q = 10 | m = 0.575
s = 0.00293
mr = 2.006
sr = 0.0205 | m = 0.821
s = 0.00293
mr = 2.865
sr = 0.0205 | m = 1.231
s = 0.00293
mr = 4.298
sr = 0.0205 | m = 1.395
s = 0.00293
mr = 4.871
sr = 0.0205 | m = 2.052
s = 0.00293
mr = 7.163
sr = 0.0205 |
Rocha com qualidade razoável, Descontinuidades parcialmente expostas e espaçamento de 0.3 to 1 m, RMR = 44, Q = 1 | m = 0.128
s = 0.00009
mr = 0.947
sr = 0.00198 | m = 0.183
s = 0.00009
mr = 1.353
sr = 0.00198 | m = 0.275
s = 0.00009
mr = 2.030
sr = 0.00198 | m = 0.311
s = 0.00009
mr = 2.301
sr = 0.00198 | m = 0.458
s = 0.00009
mr = 3.383
sr = 0.00198 |
Rocha com má qualidade, Várias descontinuidades expostas e espaçamento de 30 to 500 mm, RMR = 23, Q = 0.1 | m = 0.029
s = 0.000003
mr = 0.447
sr = 0.00019 | m = 0.041
s = 0.000003
mr = 0.639
sr = 0.00019 | m = 0.061
s = 0.000003
mr = 0.959
sr = 0.00019 | m = 0.069
s = 0.000003
mr = 1.087
sr = 0.00019 | m = 0.102
s = 0.000003
mr = 1.598
sr = 0.00019 |
Rocha com muito má qualidade, Várias descontinuidades extremamente expostas e espaçamento inferior a 50 mm, rocha solta de graduação fina, RMR = 3, Q = 0.01 | m = 0.007
s = 0.0000001
mr = 0.219
sr = 0.00002 | m = 0.010
s = 0.0000001
mr = 0.313
sr = 0.00002 | m = 0.015
s = 0.0000001
mr = 0.469
sr = 0.00002 | m = 0.017
s = 0.0000001
mr = 0.532
sr = 0.00002 | m = 0.025
s = 0.0000001
mr = 0.782
sr = 0.00002 |
Resistência de rochas à compressão simples σc, coeficiente de Poisson ν e peso volúmico da rocha γ
| Resistência da rocha | Tipos de rochas (exemplos) | Resistência σc [MPa] | Coeficiente de Poisson ν | Peso bruto da rocha γ [kN/m3] |
| Rocha sólida | rocha sólida mais dura, intacta, rocha de quartzo e basalto compacta e densa, outras rochas duras extraordinárias | >150 | 0.10 | 28.00 – 30.00 |
| Rocha muito dura | rocha de granito muito dura, pórfiro de quartzo, granito muito duro, xisto duro, quartzito, arenito muito duro e calcita muito dura | 100 – 150 | 0.15 | 26.00 – 27.00 |
| Rocha dura | granito, arenito e calcita muito duro, lodo de quartzito, conglomerado rígido, minério muito duro, pedra calcária dura, mármore, dolomita, pirita | 80 – 100 | 0.20 | 25.00 – 26.00 |
| Rocha | arenito, minério, xisto de areia média, laje | 50 – 80 | 0.25 | 24.00 |
| Rocha média | barro duro, arenito e calcite mole, argila calcária | 20 – 50 | 0.25 – 0.30 | 23.00 – 24.00 |
| Rocha mole | xisto, calcário macio, giz, pedra de sal, terra congelada, antracite, marga, arenito remodelado, conglomerado macio, solo com falhas | 5 – 20 | 0.3 – 0.35 | 22.00 – 26.00 |
| Solo fraco | argila compacta, eluvião do solo, carvão preto | 0.5 – 5 | 0.35 – 0.40 | 20.00 – 22.0
18.00 – 2 |
Cálculo dos Parâmetros de Hoek-Brown
Se o maciço rochoso for classificado através do GSI (Geological Structure Index), o programa pode determinar os parâmetros H-B da seguinte forma:
![]()
![]()
![]()
| onde: | GSI | – | Geological Structure Index |
| D | – | coeficiente de danos do maciço rochoso | |
| mi | – | constante de resistência do material da rocha intacta para condições de pico |
Valores do coeficiente de danos D para o talude rochoso
| Descrição do maciço rochoso | Valores sugeridos para o coeficiente D |
Explosão de pequena escala em taludes que resulta em danos ligeiros no maciço rochoso, particularmente se controlados pela explosão utilizada. No entanto, o alívio de tensão provoca alguma perturbação. (Explosão boa). | 0.7 |
Explosão de pequena escala em taludes que resulta em danos ligeiros no maciço rochoso, particularmente se controlados pela explosão utilizada. No entanto, o alívio de tensão provoca alguma perturbação. (Explosão má). | 1 |
Poços abertos e muito largos com perturbações significantes devido e explosões de produção pesadas e ao alívio de tensão da remoção de sobrecarga. (Explosão de produção). | 1 |
Em algumas rochas moles a escavação pode ser executada com recurso a maquinaria de escavação e nível de danos no talude é menor. (Escavação mecânica). | 0.7 |
Valores aproximadas para a constante de resistência do material da rocha intacta mi (segundo Hoek)
| Tipo de rocha | Exemplos de rochas | mi [–] |
| Pedras calcárias com clivagem cristalina bem desenvolvida | Dolomita, calcita, mármore | ≈ 7 |
| Rochas de argila consolidadas | Barro, silte, xisto siltoso, ardósia | ≈ 10 |
| Arenito com cristais sólidos e clivagem cristalina pouco desenvolvida | Arenito, quartzito | ≈ 15 |
| Rochas cristalinas ígneas de graduação fino | Andesita, dolerite, diabase, riólita | ≈ 17 |
| Pedras grosseiras e metamórficas | Anfibolito, gabro, gneisse, granito, diorite | ≈ 25 |
Barton – Bandis
O critério de rotura da resistência ao cisalhamento de Barton-Bandis para maciços rochosos é dado por:
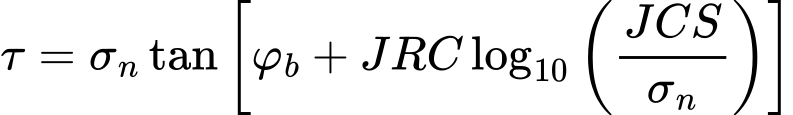
| onde: | JRC | – | coeficiente de rugosidade da junta |
| σn | – | tensão normal atuante na superfície da junta da rocha | |
| JCS | – | resistência à compressão da junta | |
| φb | – | ângulo de atrito interno básico da superfície de deslizamento |
Se possível, os parâmetros de resistência ao cisalhamento devem ser determinados a partir de ensaios de campo. Intervalos aproximados dos parâmetros do critério de rotura de Barton-Bandis estão disponíveis aqui.
Parâmetros de Barton – Bandis
Coeficiente de rugosidade da junta JRC
Se o valor de JRC não puder ser determinado diretamente a partir de ensaios na superfície da junta, é possível obter este valor a partir do gráfico de Barton (ver figura), que mostra a variação do coeficiente JRC em função do comprimento do perfil e da profundidade da rugosidade.
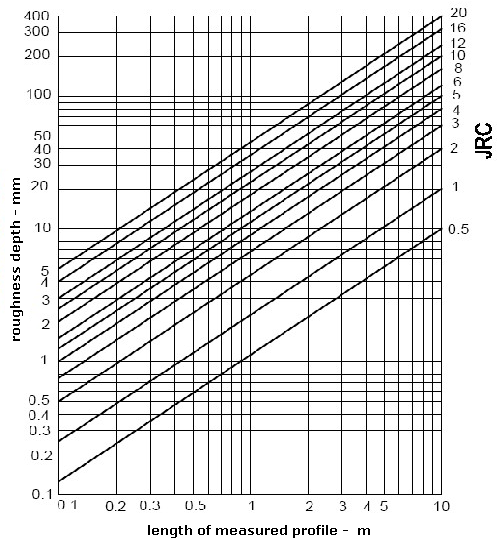 Diagrama para determinar JRC (segundo Barton)
Diagrama para determinar JRC (segundo Barton)
Perfis da rugosidade de juntas com os intervalos típicos de JRC.
 Perfis da rugosidade de juntas com os intervalos típicos de JRC (Barton & Chubey 1977)
Perfis da rugosidade de juntas com os intervalos típicos de JRC (Barton & Chubey 1977)
Resistência à compressão da descontinuidade JCS
Os métodos que permitem determinar a resistência à compressão da descontinuidade (superfície de deslizamento) são geralmente recomendados por ISRM. O valor de JCS pode ser obtido a partir do gráfico de Deere-Miller, que mostra a sua dependência em relação à resistência da rocha segundo os ensaios de martelo de Schmidt, ver figura abaixo.
Ângulo de atrito interno básico da superfície de deslizamento φb
O valor básico do ângulo de atrito da superfície é aproximadamente igual ao valor residual φr . No entanto, pode ser assumido em laboratórios ao utilizar instrumentos de medição de cisalhamento (a área típica da amostra é 50*50 mm). O intervalo típico para o ângulo de atrito interno básico de superfícies rochosas expostas é 25° a 35°.
Peso Volúmico de Rochas
Peso volúmico de rochas γ| Resistência da rocha | Categoria da rocha (exemplos) | Peso volúmico da rocha γ [kN/m3] |
| Rocha sólida | rocha sólida mais dura, intacta, rocha de quartzo e basalto compacta e densa, outras rochas duras extraordinárias | 28.0 – 30.0 |
| Rocha muito dura | rocha de granito muito dura, pórfiro de quartzo, granito muito duro, xisto duro, quartzito, arenito muito duro e calcita muito dura | 26.0 – 27.0 |
| Rocha dura | granito, arenito e calcite muito duro, filão de quarzite, conglomerado duro, minério muito duro, calcário duro, mármore, dolomita, pirite | 25.0 – 26.0 |
| Rocha | arenito, minério, xisto arenoso médio, laje | 24.0 |
| Rocha média | barro duro, arenito e calcite mole, argila calcária | 23.0 – 24.0 |
| Rocha mole | xisto, calcário macio, giz, pedra de sal, terra congelada, antracite, marga, arenito remodelado, conglomerado macio, solo com falhas | 22.0 – 26.0 |
| Solo fraco | argila compacta, eluvião do solo, carvão preto | 20.0 – 22.0 18.0 – 20.0 |
Influência de Efeitos Sísmicos
O programa considera os efeitos sísmicos através de duas variáveis – fator de aceleração horizontal Kh e fator de aceleração vertical Kv. O fator de aceleração é um valor adimensional que representa a aceleração sísmica como uma fração da aceleração gravítica. Os efeitos sísmicos são introduzidos através da força sísmica S, que é determinada a partir da multiplicação do peso da rocha sujeita ao sismo (isto é, o bloco de rocha) pelo fator de aceleração. Ao assumir o efeito sísmico apenas na direção horizontal, a força sísmica é dada por:![]()
| onde: | Kh | – | fator de aceleração horizontal |
| W | – | peso do maciço rochoso |
| Escala M_C_S | Aceleração horizontal | Fator de aceleração horizontal |
| ((MSK-64) | [mm/s2] | Kh |
| 1 | 0.0 – 2.5 | 0.0 – 0.00025 |
| 2 | 2.5 – 5.0 | 0.00025 – 0.0005 |
| 3 | 5.0 – 10.0 | 0.0005 – 0.001 |
| 4 | 10.0 – 25.0 | 0.001 – 0.0025 |
| 5 | 25.0 -50.0 | 0.0025 – 0.005 |
| 6 | 50.0 – 100.0 | 0.005 – 0.01 |
| 7 | 100.0 – 250.0 | 0.01 – 0.025 |
| 8 | 250.0 – 500.0 | 0.025 – 0.05 |
| 9 | 500.0 -1000.0 | 0.05 -0.1 |
| 10 | 1000.0 -2500.0 | 0.1 -0.25 |
| 11 | 2500.0 -5000.0 | 0.25 -0.5 |
| 12 | > 5000.0 | > 0.5 |

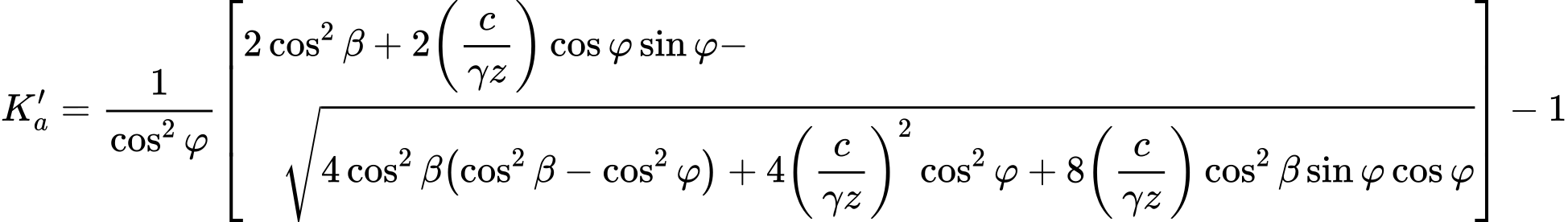
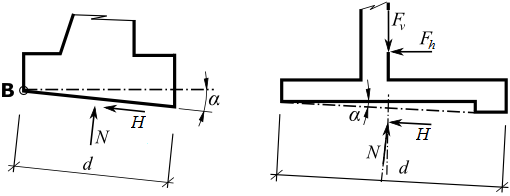
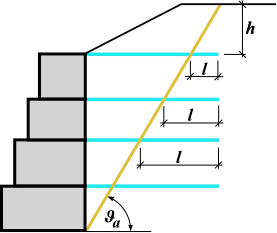
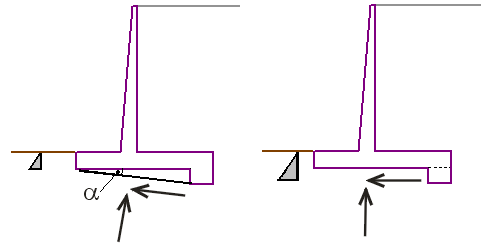
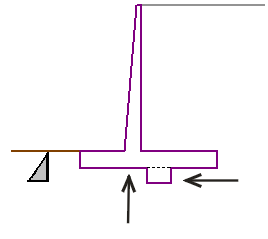
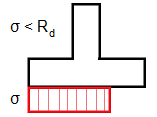
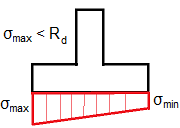
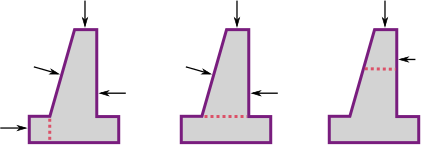
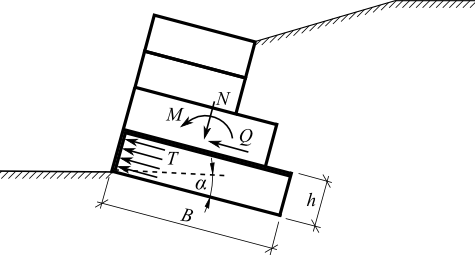
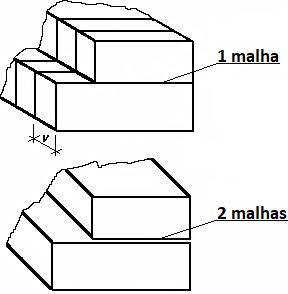
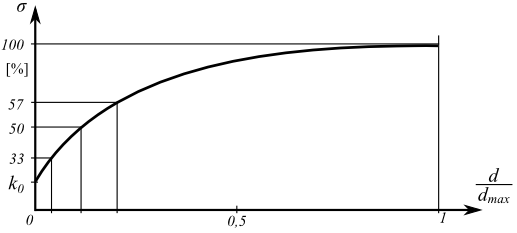
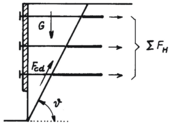
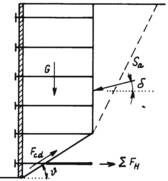
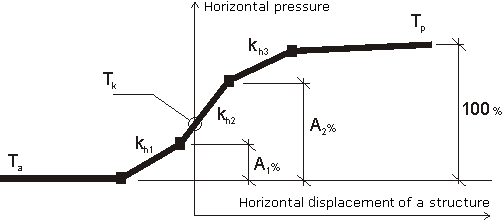
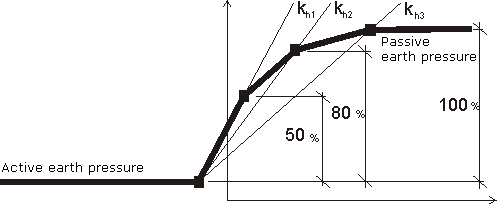
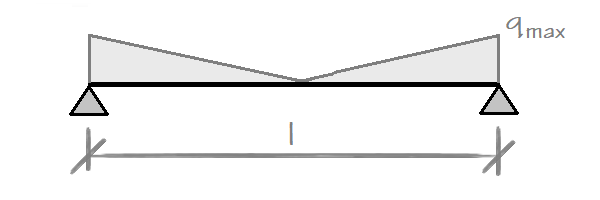
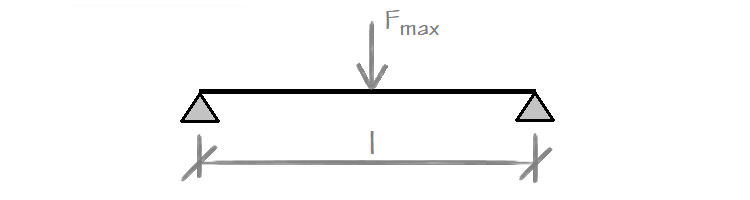
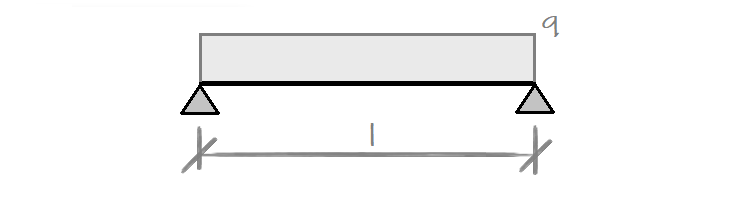
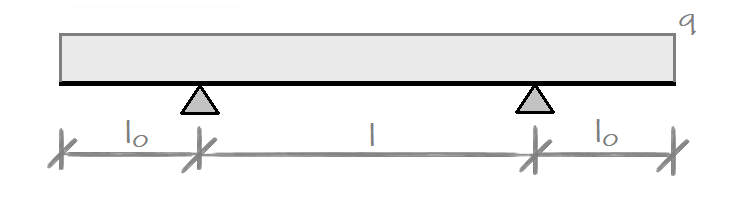
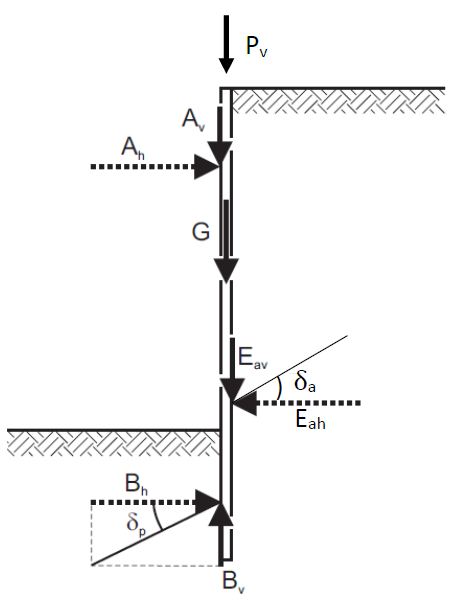
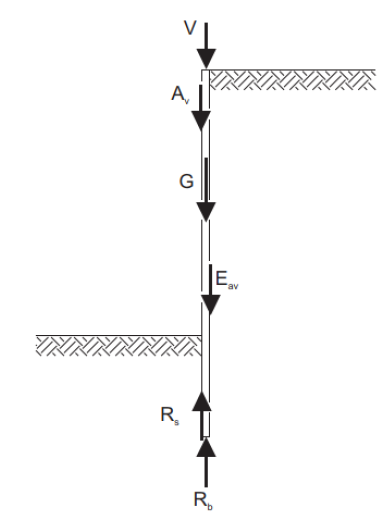
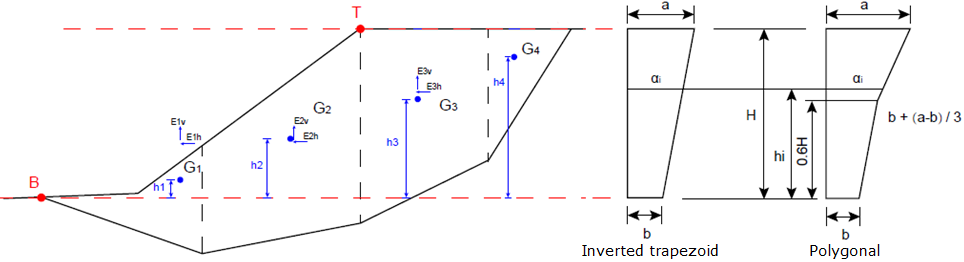
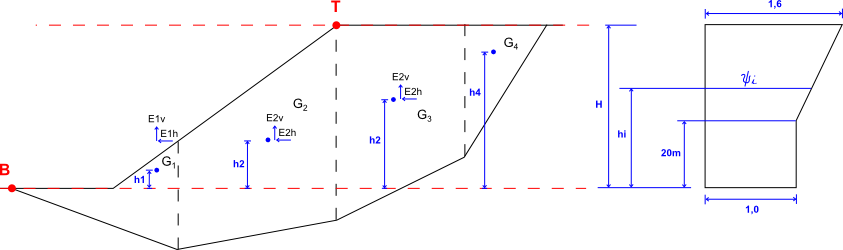

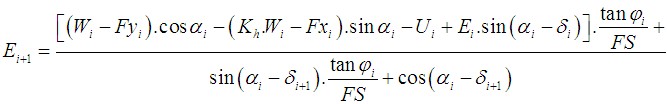
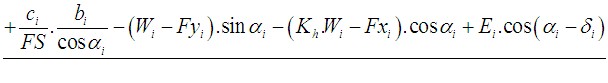
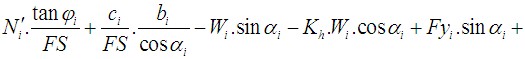
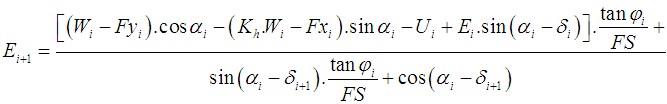
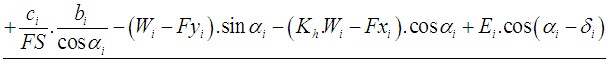
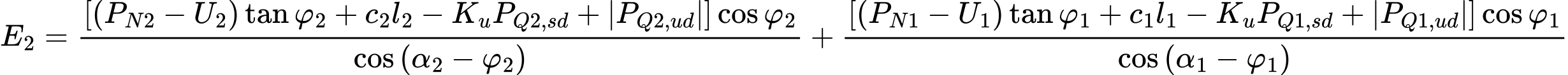
 Teste o software GEO5.
Teste o software GEO5.
