Estaca via CPT/SPT
O programa Estaca via CPT permite:
![]() calcular a capacidade de suporte a partir de ensaios CPT
calcular a capacidade de suporte a partir de ensaios CPT
![]() calcular assentamentos a partir de ensaios CPT
calcular assentamentos a partir de ensaios CPT
![]() calcular a capacidade de suporte a partir de ensaios SPT
calcular a capacidade de suporte a partir de ensaios SPT
Análises através de CPTs
O programa Estaca via CPT permite verificar a capacidade de suporte e assentamento de uma estaca isolada ou de um grupo de estacas, com base nos resultados de ensaios de penetração – CPTs.
O principal objetivo é determinar as capacidade de suporte da base e do furo. Esta análise pode ser realizada de acordo com as seguintes Normas e métodos:
![]() EN 1997-2
EN 1997-2
![]() NEN 6743
NEN 6743
![]() LCPC (Bustamante)
LCPC (Bustamante)
![]() Schmertmann
Schmertmann
![]() NBN EN1997-1 ANB
NBN EN1997-1 ANB
Em todos os métodos, os parâmetros essenciais a introduzir são coeficientes adimensionais para ajustar o valor da capacidade de suporte e o atiro do furo. Podem ser encontradas nomenclaturas diferentes para estes parâmetros em diferentes publicações. No programa Estaca via CPT é utilizada a seguinte nomenclatura:
| αp | – | coeficiente de atrito da base da estaca |
| αs | – | coeficiente de atrito do furo |
Estes coeficientes são calculados automaticamente, com base no tipo de estaca e do solo envolvente – estes parâmetros podem ser especificados manualmente (αp pode ser introduzido na janela “Geometria”, αs como um parâmetro do solo).
Ao analisar estacas retangulares, o coeficiente da forma da estaca s é introduzido para reduzir a capacidade de suporte da base. Ao analisar estacas com alargamento, o coeficiente da influência da base alargada β é introduzido para ajustar a capacidade de suporte da base alargada da estaca. Ao calcular a capacidade de suporte da base, o programa considera a influência das mudanças na elevação do terreno automaticamente.
O programa permite o cálculo da curva carga-assentamento e do assentamento para um dado carregamento. Esta análise adota os valores calculados para as capacidades de suporte da base da estaca e do furo, de acordo com a Norma NEN 6743. Também pode ser considerada um atrito superficial negativo ao calcular o assentamento da estaca.
A verificação da capacidade de suporte depende da metodologia de verificação selecionada na secção “Estaca via CPT”.
Capacidade de Suporte
A capacidade de suporte máxima de uma estaca isolada, com base nos valores da resistência da ponta qc do iésimo ensaio de penetração de cone, é dada por:
![]()
| onde: | Fmax, i | – | capacidade de suporte máxima da estaca do iésimo CPT |
| Fmax,base,i | – | resistência máxima da base do iésimo CPT | |
| Fmax,shaft,i | – | resistência máxima do furo do iésimo CPT |
Se a análise for realizada de acordo com o fator de segurança ou com a teoria dos estados limite, a capacidade de suporte de uma estaca isolada é obtida como uma média aritmética das n capacidades de suporte calculadas:
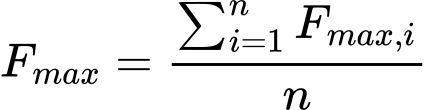
Se a análise for realizada de acordo com EN 1997-2, ou com NBN EN1997-1 ANB, a capacidade de carga final depende dos coeficientes de correlação ξ3 e ξ4.
Se a análise for realizada de acordo com a Norma NEN 6743, o método para considerar vários ensaios CPT é diferente e segue o proposto na Norma NEN 6743 (artigo 5.3.2.2).
A resistência máxima da base da estaca Fmax,base é dada por:
![]()
| onde: | Abase | – | área da secção transversal da base da estaca |
| pmax, base | – | pressão máxima na base da estaca obtida a partir de ensaios CPT |
A resistência máxima do furo Fmax,shaft é dada por:
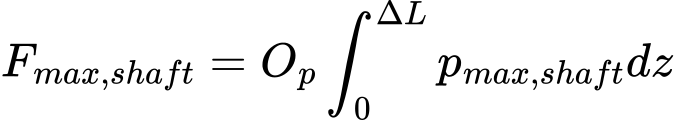
| onde: | Op | – | periferia da estaca do solo de suporte |
| pmax, shaft | – | força máxima no furo (atrito) obtida a partir de ensaios CPT | |
| ΔL | – | comprimento da estaca, quer o comprimento para o atrito ativo do furo ou o comprimento para a base alargada | |
| z | – | dimensão vertical ao longo do eixo da estaca |
Cálculo da pressão máxima na base da estaca pmax,base e a força máxima desenvolvida ao longo do furo pmax,shaft (determinadas de acordo com o tipo de análise selecionado na secção “Estaca via CPT”).
EN 1997-2
A Norma EN 1997-2 determina que a pressão máxima na base da estaca (resistência máxima) pmax, base, do iésimo ensaio de penetração, é dada por:
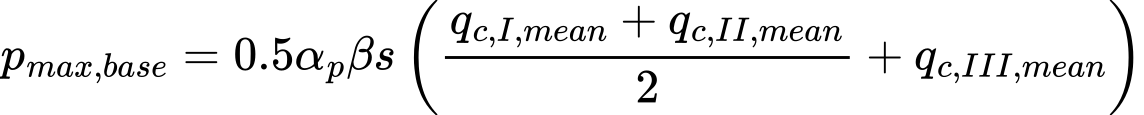
| onde: | qc, I, mean | – | média dos valores qc, I (ver Addendum D.7 em EN 1997-2) |
| qc, II, mean | – | média das resistências da ponta do cone mínimas qc, II (ver Addendum B4 em EN 1997-3) | |
| qc, III, mean | – | média das resistências da ponta do cone qc, III (ver Addendum B4 em EN 1997-3) | |
| αp | – | coeficiente da base da estaca (fator da classe da estaca) | |
| s | – | coeficiente da forma da estaca | |
| β | – | coeficiente da base alargada da estaca |
O valor máximo da pressão de penetração qc é limitado pelo valor de 15 MPa. Em solos não coesivos, a análise considera a influência da sobreconsolidação (OCR).
O atrito máximo do furo (resistência do furo) pmax, shaft é dado por:
![]()
| onde: | αs | – | coeficiente do atrito do furo |
| qc, z, a | – | resistência da ponta à profundidade h |
Bibliografia:
EN 1997-2 Geotechnical design. Ground investigation and testing.
NEN 6743
A Norma NEN 6743 “Fundações por Estacas” determina a pressão máxima na base da estaca pmax, base, a partir do iésimo ensaio de penetração, é calculada atráves da seguinte expressão:
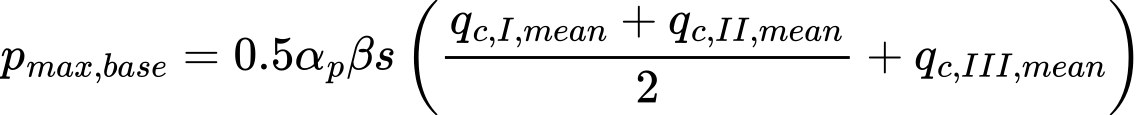
| onde: | qc, I, mean | – | média dos valores qc, I (ver artigo 5.3.3.3 da Norma NEN 6743) |
| qc, II, mean | – | média das resistências da ponta do cone mínimas qc, II (ver artigo 5.3.3.3 da Norma NEN 6743) | |
| qc, III ,mean | – | média das resistências da ponta do cone qc, III (ver artigo 5.3.3.3 da Norma NEN 6743) | |
| αp | – | coeficiente da base da estaca | |
| s | – | coeficiente da forma da estaca | |
| β | – | coeficiente da base alargada da estaca |
O valor máximo da pressão de penetração qc é limitado pelo valor de 15 MPa. Em solos não coesivos, a análise considera a influência da sobreconsolidação (OCR).
O atrito máximo do furo (resistência do furo) pmax, shaft é dado por:
![]()
| onde: | αs | – | coeficiente do atrito do furo |
| qc, z, a | – | resistência da ponta à profundidade h |
Bibliografia:
NEN 6743:1991/A1:1997, Geotechniek – Berekeningsmethode voor funderingen op palen – Drukpalen.
LCPC (Bustamante)
O método de LCPC – Laboratoire Central des Ponts et Chausees (também conhecido como método de Bustamante, baseado nos trabalhos de Bustamante e Gianeselli) determina a pressão máxima na base da estaca pmax, base como:
![]()
| onde: | αp | – | coeficiente da base da estaca |
| qc, eq | – | resistência média equivalente da ponta do cone |
O atrito máximo do furo (resistência do furo) pmax, shaft é dado por:
![]()
| onde: | αs | – | coeficiente do atrito do furo |
| qc, z, a | – | resistência da ponta |
Determinação da Resistência Média Equivalente da Ponta do Cone
A resistência média equivalente da ponta do cone é obtida através do procedimento seguinte:
| 1) | Calcular a resistência média da ponta qc, mean na ponta da estaca, através da média dos valores qc acima da zona compreendida entre 1.5d abaixo da ponta da estaca até 1.5d acima da ponta da estaca (d é o diâmetro da estaca) |
| 2) | Eliminar os valores qc dentro da zona compreendida entre os valores que são superiores a 1.3 vezes a média da resistência da ponta do cone qc, mean e os valores que são 0.7 vezes inferiores qc, mean, conforme mostra a figura |
| 3) | Calcular a resistência média equivalente da ponta do cone qc, eq, através da média dos valores restantes da resistência da ponta do cone qc, fora das zonas referidas acima, que não foram eliminados (isto é, valores dentro do intervalo 0.7 a 1.3 vezes a resistência da ponta do cone qc, mean). |
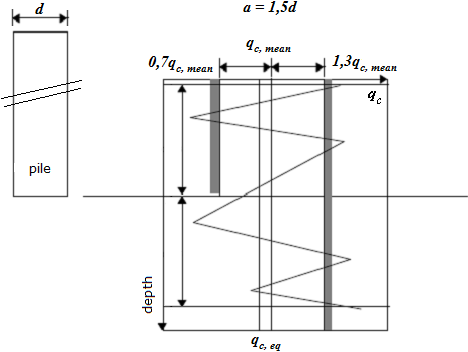 Determinação da resistência média equivalente da ponta do cone qc, eq
Determinação da resistência média equivalente da ponta do cone qc, eq
Bibliografia:
Tom Lunne, Peter K. Robertson, John J.M. Powell: Cone Penetration Testing in Geotechnical Practice, Spon Press, 1997, London.
Schmertmann
O método de Schmertmann determina a pressão máxima na base da estaca pmax, base através da seguinte expressão:
![]()
| onde: | αp | – | coeficiente da base da estaca |
| qupr | – | resistência média modificada da ponta do cone |
![]()
| onde: | qc1, qc2 | – | valor mínimo da média da resistência da ponta do cone |
Em solos não coesivos, a análise considera a influência da sobreconsolidação (OCR).
O atrito máximo do furo (resistência do furo) pmax, shaft é dado por:
![]() para solos não coesivos:
para solos não coesivos:
![]()
| onde: | K | – | coeficiente de correlação do atrito superficial |
| – | valor médio da manga de atrito local do penetrómetro fs dentro do intervalo definido entre parêntesis na expressão | ||
| As | – | área da superfície do furo da estaca dentro do intervalo | |
| d | – | diâmetro da estaca | |
| D | – | comprimento enterrado da estaca |
![]() para solos coesivos:
para solos coesivos:
![]()
| onde: | αs,i | – | coeficiente de atrito do furo segundo Tomlinson na iésima camada |
| – | valor médio da manga de atrito local do penetrómetro fs na iésima camada | ||
| As,i | – | área da superfície do furo da estaca na iésima camada |
Bibliografia:
Schmertmann J.H.: Guidelines for Cone Penetration Test, Performance and deign, U.S. Departments of Transportation, report No. FHWA-TS-78-209, Washington,D.C., 1978.
Determinação da Resistência da Ponta do Cone Média
O valor médio mínimo da resistência da ponta do cone qc é determinado através do valor mínimo da média da resistência da ponta do cone qc acima da zona influenciada, entre 0.7d a 4d abaixo da base da estaca (d é o diâmetro da estaca). O valor médio mínimo da resistência da ponta do cone qc2 é determinado acima da zona de influência, que se estende a partir de 8d acima da base da estaca (d é o diâmetro da estaca). O procedimento para obter o valor médio da resistência da ponta do cone qc1, qc2 é o seguinte (ver figura):
| 1) | determinar duas médias da tensão do cone, dentro da zona abaixo da base da estaca, uma para a zona à profundidade de 0.7d e a outra à profundidade de 0.4d ao longo da linha entre “a” e “b“. O menor dos dois valores é conservado. (A zona com profundidade 0.7d aplica-se onde a tensão do cone aumenta com a profundidade abaixo da base da estaca). |
| 2) | determinar a tensão do cone mais reduzida dentro da zona descrita no passo 1 |
| 3) | determinar a média dos dois valores obtidos nos passos 1 e 2. O passo 4 é determinar a tensão média do cone dentro da zona |
| 4) | determinar a tensão média do cone dentro da zona 8d acima da base da estaca, que permite obter o valor qc. Finalmente, a média dos valores dos passos 3 e 4 é determinada |
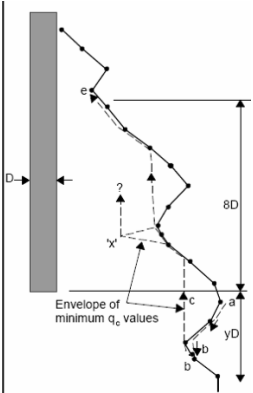 Determinação da resistência média da ponta do cone qc1, qc2
Determinação da resistência média da ponta do cone qc1, qc2
Coeficiente de Correlação K
O coeficiente de correlação do atrito superficial K é introduzido na secção “Estaca via CPT”. O valor deste coeficiente é igual ao rácio entre a resistência unitária do fura da estaca e o atrito unitário local da manga do penetrómetro. O coeficiente de correlação K pode ser expresso, por exemplo, como função do comprimento enterrado da estaca – ver os gráficos seguintes.
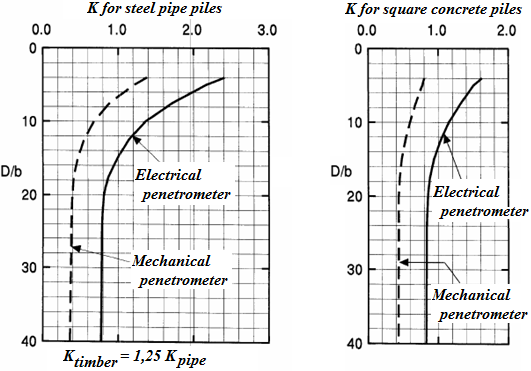 Função do comprimento enterrado da estaca (D – comprimento enterrado da estaca, b – largura ou diâmetro da estaca)
Função do comprimento enterrado da estaca (D – comprimento enterrado da estaca, b – largura ou diâmetro da estaca)
Bibliografia:
FHWA HI 97-013: Design and Construction of Driven Pile Foundations, Workshop manual – Volume 1, National Highway institute.
NBN EN 1997-1 ANB
A Norma NBN EN 1997-1 ANB determina a pressão máxima na base da estaca (resistência máxima) pmax, base para o iésimo ensaio de penetração correspondente, de acordo com:
![]()
| onde: | αp | – | coeficiente da base da estaca |
| εp | – | fator de escala | |
| β | – | coeficiente da base da estaca expandida | |
| s | – | coeficiente de forma da estaca | |
| qp | – | resistência unitária da base da estaca de acordo com o método de De Beer |
O Fator de Escala εp é determinado de acordo com:
– para solos terciários de OC-argila:
![]()
– para outros tipos de solo:
![]()
| onde: | Db,eq | – | diâmetro equivalente da base da estaca |
| Dc | – | diâmetro do cone CPT |
O atrito máximo da vala (resistência da vala) pmax, shaft é obtido através de:
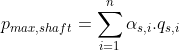
| onde: | αs, i | – | coefciente de atrito da vala na iésima camada |
| qs,i | – | atrito médio da vala na iésima camada | |
| n | – | número de camadas atravessadas pela estaca |
O atrito médio da vala qs,i é determinado de acordo com:
![]()
| onde: | qc,m,i | – | resistência média do cone (qc) na iésima camada |
| ηpi | – | coeficiente de atrito empírico |
O coeficiente de atrito empírico ηpi (ou atrito médio da vala máximo) é determinado de acordo com o tipo de solo e conforme a tabela seguinte:
| Tipo de Solo | qc,m,i [MPa] | ηpi [-] or qs,i [kPa] | |
| Argila | 1 to 4,5 | – | ηpi = 1/30 |
| > 4,5 | qs,i = 150 | ||
| Silte | 1 to 6 | ηpi = 1/60 | |
| > 6 | qs,i = 100 | ||
| Argila arenosa | 1 to 10 | ηpi = 1/80 | |
| > 10 | qs,i = 125 | ||
| Areia | 1 to 10 | ηpi = 1/90 | |
| 10 to 20 | qs,i = 110+4(qc,m,i – 10) | ||
| > 20 | qs,i = 150 |
Bibliografia:
RICHTLIJNEN VOOR DE TOEPASSING VAN DE EUROCODE 7 IN BELGIË VOLGENS DE NBN EN 1997-1 ANB (WTCB Rapport nr. 20 – November 2020).
Método De Beer
Este método determina a resistência unitária na base da estaca. O método baseia-se no “efeito de escala” para o ensaio CPT e para a base da estaca.
O método está descrito conforme os passos seguintes, que são realizados a cada 0.2m ao longo do comprimento da estaca.
1) O cálculo de ângulo de atrito interno φ é realizado de acordo com a fórmula (1)
![]()
| onde: | qc | – | resistência da ponta do cone |
| σeff | – | tensão efetiva | |
| φ | – | ângulo de atrito interno |
2) O Cálculo dos ângulos βc e βp é realizado de acordo com as fórmulas (2) e (3).
![]()
![]()
Nota: Ambos os ângulos βc e βp não podem exceder os 90°.
| onde: | h | – | profundidade |
| dc | – | diâmetro do cone CPT | |
| D | – | diâmetro da base da estaca | |
| δ | – | coeficiente de forma da base da estaca |
Para estacas circulares e quadradas:
![]()
Para estacas retangulares:
![]()
| onde: | B | – | lado menor da base da estaca |
| L | – | lado maior da base da estaca |
3) O cálculo dos valores homogéneos qp(1) é realizado de acordo com a fórmula (4).
![]()
4) O cálculo dos valores de redução qp, j+1 é realizado de acordo com a fórmula (5).
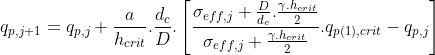
| onde: | a | – | intervalo da medição |
| hcrit | – | profundidade crítica | |
| γ | – | peso volúmico do solo | |
| qp(1), crit | – | valor homogéneo para a profundidade crítica hcrit |
A profundidade crítica hcrit depende do diâmetro da base da estaca D e do ângulo de atrito interno φ:
Para estacas D < 0,4 m
– hcrit = 0,2 m
Para estacas 0,4 m ≤ D ≤ 0,6 m
– hcrit = 0,2 m para φ < 32,5°
– hcrit = 0,2 m e 0,4 m para φ ≥ 32,5°
Para estacas D ≥ 0,6 m
– hcrit = 0,2 m para φ < 32,5°
– hcrit = 0,2 m e 0,4 m para 32,5° ≤ φ < 37,5°
– hcrit = 0,2 m, 0,4 m e 0,6 m para φ ≥ 37,5°
Nota: O valor de redução final é o menor para todas as profundidades críticas.
Nota: O valor de redução deve ser igual ou inferior ao valor homogéneo.
5) O cálculo dos valores de maximização qp, q+1 é realizado de acordo com a fórmula (6).
![]()
Nota: O valor de maximização deve ser igual ou inferior ao valor redução.
6) O cálculo de valores mistos qr,b deve ser realizado como uma média dos n valores de maximização qp, q+1. A resistência unitária da base da estaca é o valor misto para o nível da base da estaca.
![]()
Nota: O valor misto deve ser igual ou inferior ao valor homogéneo.
Bibliografia:
Prof. Dr. ir E. DE BEER: METHODES DE DEDUCTION DE LA CAPACITE PORTANTE D´UN PIEU A PARTIR DES RESULTATS DES ESSAIS DE PENETRATION (MEMOIRES – VERHANDELINGEN), online: https://www.bggg-gbms.be/l/library/download/urn:uuid:05c758bb-bf51-4eb7-9dc0-5a03b293f7e0/overige+publicaties.pdf?format=save_to_disk&ext=.pdf
Diâmetro Equivalente da Base da Estaca
O diâmetro equivalente da base da estaca Db,eq é definido de acordo com a Norma NBN EN 1997-1 ANB:
– para estacas circulares
![]()
– para estacas quadradas ou retangulares
![]() se b ≤ 1,5a
se b ≤ 1,5a
![]()
![]() se b > 1,5a
se b > 1,5a
![]()
| onde: | D | – | diâmetro da base da estaca |
| a | – | lado menor da base da estaca | |
| b | – | lado maior da base da estaca |
Atrito Superficial Negativo
O atrito superficial negativo é um efeito provocado pelo assentamento do solo que envolve a estaca. A deformação do solo à volta da estaca tende a puxar a estaca para baixo, reduzindo a sua capacidade de suporte. Em casos extremos, este efeito pode eliminar por completo à influência do atrito do furo. A estaca fica, então, suportada apenas pelo subsolo elástico abaixo da sua base.
O atrito superficial negativo Fs,nk,rep é dado por:
![]()
| retained: | Op | – | periferia da estaca |
| n | – | número da camadas dentro da zona de atrito negativo | |
| hi | – | profundidade da iésima camada | |
| K0,i,rep | – | valor representativo do coeficiente do empuxo de terra em repouso | |
| δi,rep | – | atrito entre o solo e a estaca na iésima camada | |
| φi,rep | – | valor representativo do ângulo de atrito interno na iésima camada | |
| σv,i-1,rep | – | tensão horizontal no solo na i-1 camada | |
| σv,1,rep | – | tensão horizontal no solo na iésima camada | |
| pi,a,rep | – | sobrecarga na iésima camada | |
| Δσi,v,w,rep | – | variação da tensão vertical σv na iésima camada | |
| tendo em conta a seguinte relação: | |||
Se a superfície de deslizamento estiver definida, o valor do atrito superficial negativo Fs,nk,rep é dado por:
![]()
| retained: | Op | – | periferia da estaca |
| hi | – | profundidade da iésima camada | |
| ci,rep | – | coesão representativa da superfície de deslizamento | |
| – para betume 10*103 N/m2 | |||
| – para bentonite 20*103 N/m2 | |||
| – para material sintético 50*103 N/m2 |
O valor da coesão representativa ao longo da superfície de deslizamento também pode ser introduzido diretamente pelo usuário.
Coeficiente de Atrito do Furo ALFAs
O coeficiente que reduz o atrito do furo αs difere consoante o método aplicado e o tipo de solo. Os valores destes coeficientes estão disponíveis no programa de acordo com as Normas EN 1997-2 e NEN 6743.
Os valores para areias e areias com cascalho estão listados nas tabelas seguintes:
| Estacas | NEN 6743 αs [–] | EN 1997-2 αs [–] |
| Estacas cravadas pré-fabricadas ou estacas metálicas | 0.010 | 0.010 |
| Estacas Franki | 0.014 | 0.012 |
| Estacas cravadas em madeira | 0.012 | 0.012 |
| Estacas vibradas ou vibro-pressionadas | 0.012 | 0.012 |
| Estacas parafuso realizadas no local | 0.009 | 0.009 |
| Estacas parafuso pré-fabricadas | 0.009 | 0.009 |
| Estacas parafuso realizadas no local com reboco adicional | 0.006 | 0.006 |
| Estacas parafuso pré-fabricadas com reboco adicional | 0.006 | 0.006 |
| Estacas tubulares metálicas | 0.0075 | 0.0075 |
| Estacas de hélice contínua (CFA) | 0.006 | 0.006 |
| Estacas escavadas ou estacas contidas por bentonite suspensa | 0.006 | 0.006 |
| Estacas escavadas com revestimento metálico | 0.005 | 0.005 |
Para areias de graduação muito grosseira e cascalhos, os valores superiores são reduzidos, em ambos os métodos, através do coeficiente de redução (0.75 para areia de graduação grosseira, 0.5 para cascalho).
Para turfa, considera-se o valor de αs = 0.
Para argila e silte os valores de αs de acordo com EN 1997-2 estão listados na tabela seguinte:
| Tipo de Solo | qc [MPa] | αs [–] |
| argila | > 3 | < 0.030 |
| argila | < 3 | < 0.020 |
| silte | < 0.025 |
For argila e silte, os valores de αs de acordo com NEN 6743 estão listados na tabela seguinte:
| qc [MPa] | αs [–] |
| > 1 | 0.035 |
| < 1 | 0.0 profundidade para 5 vezes o diâmetro da estaca |
| 0.025 profundidade para 5 a 20 vezes o diâmetro da estaca | |
| 0,035 profundidade superior a 20 vezes o diâmetro da estaca |
Se o método LCPC (Bustamante) for utilizado para o coeficiente de atrito do furo αs, este depende da resistência da ponta qc (a tabela seguinte apresenta valores de referência).
Valores de referência para o coeficiente de atrito do furo αs com base na resistência da ponta do cone qc
| LCPC (Bustamante) Tipo de solo | Tensão do cone (resistência da ponte) qc [MPa] | αs para estacas do tipo “A” | αs para estacas do tipo “B” | Resistência máxima do furo [kPa] |
| Argila | < 1 | 0.033 | 0.033 | 15 |
| 1 < qc < 5 | 0.025 | 0.011 | 35 | |
| 5 < qc | 0.017 | 0.008 | 35 | |
| Areia | qc< 5 | 0.010 | 0.008 | 35 |
| 5 < qc < 12 | 0.010 | 0.005 | 80 | |
| 12 < qc | 0.007 | 0.005 | 120 |
O tipo “A” incluí os seguintes tipos de tecnologia de execução de estacas:
![]() parafuso (executadas no local, pré-fabricadas, executadas no local com reboco adicional, pré-fabricadas com reboco adicional, CFA, escavadas ou contidas com bentonite suspensa)
parafuso (executadas no local, pré-fabricadas, executadas no local com reboco adicional, pré-fabricadas com reboco adicional, CFA, escavadas ou contidas com bentonite suspensa)
![]() cravadas prefabricadas
cravadas prefabricadas
O tipo “B” incluí os seguintes tipos de tecnologia de execução de estacas:
![]() cravadas em aço
cravadas em aço
![]() Franki
Franki
![]() vibradas
vibradas
![]() tubulares metálicas
tubulares metálicas
![]() escavadas com revestimento metálico
escavadas com revestimento metálico
Ao utilizar o método de Schmertmann, considera-se o coeficiente αs que reduz o atrito do furo, segundo Tomlinson. Os valores utilizados no programa são derivados do seguinte gráfico, publicado em M. J. Tomlinson: Pile Design and Construction Practice (1994).
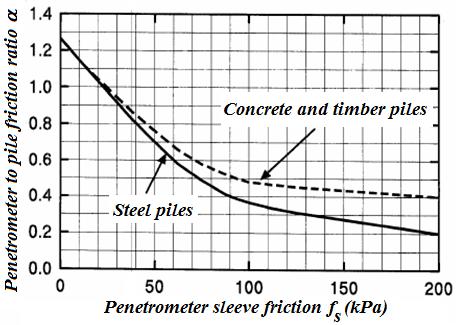
Para a Norma NBN EN 1997-1 ABN, os coeficientes são considerados de acordo com o seguinte:
| Estacas |
αs [–] |
αs,tert. clay [–] |
| Estacas cravadas pré-fabricadas ou estacas metálicas | 0.6 | 0.6 |
| Estacas Franki | 1.0 | 0.9 |
| Estacas cravadas em madeira | 1.15 | 1.15 |
| Estacas vibradas ou vibro-pressionadas | 0.6 | 0.6 |
| Estacas parafuso realizadas no local | 0.6 | 0.6 |
| Estacas parafuso pré-fabricadas | 0.6 | 0.6 |
| Estacas parafuso realizadas no local com reboco adicional | 0.6 | 0.6 |
| Estacas parafuso pré-fabricadas com reboco adicional | 0.6 | 0.6 |
| Estacas tubulares metálicas | 0.6 | 0.6 |
| Estacas de hélice contínua (CFA) | 0.5 | 0.3 |
| Estacas escavadas ou estacas contidas por bentonite suspensa | 0.5 | 0.5 |
| Estacas escavadas com revestimento metálico | 0.5 | 0.3 |
Bibliografia:
Tomlinson M. J.: Pile Design and Construction Practice, 4th edition, Taylor and Francis, 1994, ISBN 0 419 18450 3.
RICHTLIJNEN VOOR DE TOEPASSING VAN DE EUROCODE 7 IN BELGIË VOLGENS DE NBN EN 1997-1 ANB (WTCB Rapport nr. 20 – November 2020)
Influência da Sobreconsolidação (OCR)
Para areia e cascalho, a pressão máxima na base da estaca pmax,base (determinada de acordo com o tipo de análise selecionado na secção “Estaca via CPT”) é reduzida consoante o valor da sobreconsolidação OCR (definida como um parâmetro do solo na janela “Solos”), da seguinte forma:
Análise de acordo com EC 7-3, NEN 6743:
![]() para todos os solos não coesivos, a pressão máxima na base da estaca pmax,base é 15 MPa
para todos os solos não coesivos, a pressão máxima na base da estaca pmax,base é 15 MPa
![]() para OCR ≤ 2, não é realizada nenhuma redução
para OCR ≤ 2, não é realizada nenhuma redução
![]() para 2 < OCR ≤ 4, a pressão máxima na base da estaca pmax,base é multiplicada por 0.67
para 2 < OCR ≤ 4, a pressão máxima na base da estaca pmax,base é multiplicada por 0.67
![]() para OCR > 4, a pressão máxima na base da estaca pmax,base é multiplicada por 0,50
para OCR > 4, a pressão máxima na base da estaca pmax,base é multiplicada por 0,50
Ao utilizar o método de Schmertmann, a redução é realizada de acordo com o gráfico seguinte:
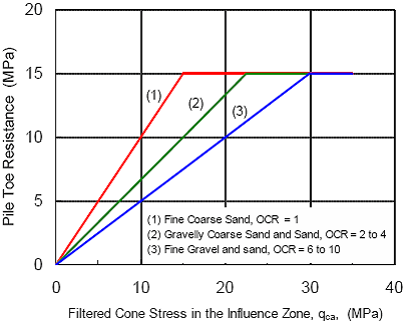 Redução da resistência média equivalente da ponta do cone de acordo com OCR (Schmertman)
Redução da resistência média equivalente da ponta do cone de acordo com OCR (Schmertman)
Coeficiente da Influência da Forma da Estaca s
Este coeficiente representa a influência de uma secção transversal retangular da estaca, particularmente do rácio b/a. O gráfico seguinte mostra os valores para este coeficiente (em função de b/a):
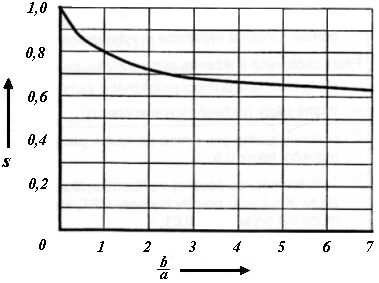 Gráfico para determinar o coeficiente de forma da estaca s (a – comprimento do lado menor, b – comprimento do lado maior)
Gráfico para determinar o coeficiente de forma da estaca s (a – comprimento do lado menor, b – comprimento do lado maior)
Para a Norma NBN EN 1997-1 ABN, o coeficiente de forma s é definido de acordo com o seguinte:
– para estacas circulares
![]()
– para estacas quadradas ou retangulares
![]()
| onde: | a | – | lado menor da base da estaca |
| b | – | lado maior da base da estaca |
Coeficiente da Influência da Base Alargada da Estaca BETA
Este coeficiente denotado de β representa a influência da base expandida da estaca, com os seus valores evidentes a partir da figura seguinte:
(como função ![]() de
de ![]() ):
):
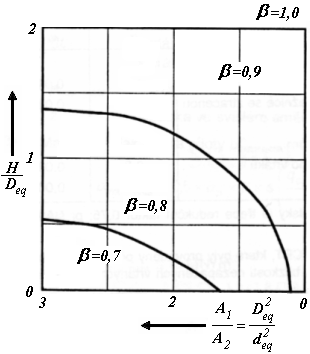 Gráfico para determinar o coeficiente β
Gráfico para determinar o coeficiente β
| onde: | H | – | comprimento da estaca [m] |
| Deq | – | diâmetro equivalente da base da estaca [m] | |
| deq | – | diâmetro equivalente da haste da estaca [m] |
Para a Norma NBN EN 1997-1 ABN, o coeficiente β é interpolado de acordo com o gráfico seguinte:
| onde: | Db,eq | – | diâmetro equivalente da base da estaca [m] |
| Ds | – | diâmetro da vala da estaca [m] |
Coeficiente de Redução da Capacidade de Suporte da Base da Estaca ALFA p
O coeficiente de redução da capacidade de suporte da base da estaca αp identifica o tipo de estaca. Os seus valores são determinados a partir de uma das metodologias de cálculo disponíveis, ou pode ser introduzido manualmente pelo usuário.
Para os métodos segundo NEN 6743 e EN 1997-2, estão disponíveis os seguintes valores para o coeficiente αp:
| Estacas | αp [–] |
| Estacas cravadas pré-fabricadas ou estacas metálicas | 1.0 |
| Estacas Franki | 1.0 |
| Estacas cravadas em madeira | 1.0 |
| Estacas vibradas | 1.0 |
| Estacas parafuso realizadas no local | 0.9 |
| Estacas parafuso pré-fabricadas | 0.8 |
| Estacas parafuso realizadas no local com reboco adicional | 0.9 |
| Estacas parafuso pré-fabricadas com reboco adicional | 0.8 |
| Estacas tubulares metálicas | 1.0 |
| Estacas de hélice contínua (CFA) | 0.8 |
| Estacas escavadas ou estacas contidas por bentonite suspensa | 0.5 |
| Estacas escavadas com revestimento metálico | 0.5 |
Para LCPC e Schmertmann, o coeficiente é calculado com base no valor da resistência do cone qc (os valores são apresentados na tabela seguinte):
Valores de referência para o coeficiente αp com base na resistência do cone qc
| LCPC (Bustamante) Tipo de solo | Resistência do cone qc [MPa] | αp para estacas escavadas | αp para estacas cravadas |
| Argila | < 1 | 0.04 | 0.50 |
| 1 < qc < 5 | 0.35 | 0.45 | |
| 5 < qc | 0.45 | 0.55 | |
| Areia | qc < 12 | 0.40 | 0.50 |
| 13 < qc | 0.30 | 0.40 |
Para a Norma NBN EN 1997-1 ANB, os valores do coeficiente αp são considerados de acordo com o seguinte:
| Estacas | αp, tert. clay [–] | αp [–] |
| Estacas cravadas pré-fabricadas ou estacas metálicas | 1,0 | 1,0 |
| Estacas Franki | 1,0 | 1,0 |
| Estacas cravadas em madeira | 1,0 | 1,0 |
| Estacas vibradas | 1,0 | 1,0 |
| Estacas parafuso realizadas no local | 0,8 | 0,5 |
| Estacas parafuso pré-fabricadas | 0,8 | 0,5 |
| Estacas parafuso realizadas no local com reboco adicional | 0,8 | 0,5 |
| Estacas parafuso pré-fabricadas com reboco adicional | 0,8 | 0,5 |
| Estacas tubulares metálicas | 1,0 | 1,0 |
| Estacas de hélice contínua (CFA) | 0,8 | 0,5 |
| Estacas escavadas ou estacas contidas por bentonite suspensa | 0,8 | 0,5 |
| Estacas escavadas com revestimento metálico | 0,8 | 0,5 |
Grupo de Estacas
A análise de um grupo de estacas depende da rigidez da estrutura. É assumido que para uma estrutura rígida, todas as estacas sofrem o mesmo assentamento, enquanto que para uma estrutura não rígida, cada estaca sofre deformações de forma independente – não é assumida nenhuma interação.
A capacidade de suporte máxima de uma fundação por estacas rígida é dada por:
![]()
| onde: | M | – | número de estacas na fundação |
| Fr,max,rep | – | capacidade de suporte de cada estaca da fundação |
Se a Norma NEN6743 for adotada, é introduzido na análise um coeficiente de redução da capacidade ξ, dependendo do número de estacas M e do número de CPTs (artigo 5.3.2.1). A capacidade de suporte máxima de uma fundação por estacas não rígida é determinada de acordo com a capacidade de suporte da maioria das estacas tensionadas do grupo, da forma seguinte:
![]()
| onde: | Fr,i | – | capacidade de suporte da estaca no grupo |
Cálculo do Assentamento da Base da Estaca
O valor do assentamento da base da estaca w1,d é determinado através da expressão:
![]()
| onde: | wbase,d | – | assentamento da base da estaca devido à força atuante |
| wbase,d,1 | – | assentamento da base da estaca devido à força atuante na base | |
| wbase,d,2 | – | assentamento da base da estaca devido à força atuante no furo | |
| wel,d | – | assentamento da estaca devido à compressão elástica |
O valor dos assentamentos wbase,.d,1 e wbase,d21 são determinados a partir de gráficos obtidos de acordo com a Norma NEN6743. O valor wel,d é dado por:
![]()
| onde: | L | – | comprimento da estaca |
| Fmean,d | – | força média atuante na estaca | |
| Aplast | – | área da secção transversal da haste da estaca | |
| Ep,mat,d | – | módulo de elasticidade do material da estaca |
Gráficos para Estimar Assentamentos
Os gráficos para determinar o assentamento são propostos pela Norma NEN6743 (artigo 6.2.1), que permitem determinar:
![]() O assentamento da estaca devido a uma força vertical na base (assentamento da estaca como percentagem do diâmetro equivalente em função da força vertical na base como percentagem da resistência máxima da base Fmax,base).
O assentamento da estaca devido a uma força vertical na base (assentamento da estaca como percentagem do diâmetro equivalente em função da força vertical na base como percentagem da resistência máxima da base Fmax,base).
![]() O assentamento da estaca devido a uma força no furo (assentamento da estaca em mm em função da força do furo como percentagem da resistência máxima do furo Fmax,shaft).
O assentamento da estaca devido a uma força no furo (assentamento da estaca em mm em função da força do furo como percentagem da resistência máxima do furo Fmax,shaft).
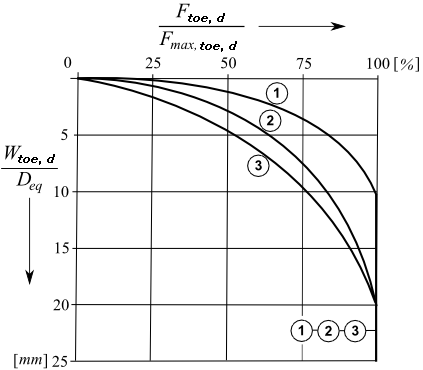 Gráfico para determinar wbase,d,1 (1 – estacas cravadas, 2 – estacas de hélice contínua, 3 – estacas escavadas)
Gráfico para determinar wbase,d,1 (1 – estacas cravadas, 2 – estacas de hélice contínua, 3 – estacas escavadas)
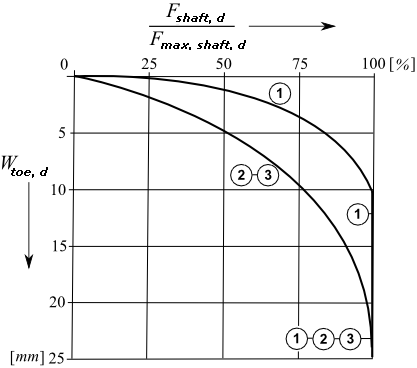 Gráfico para determinar wbase,d,2 (1 – estacas cravadas, 2 – estacas de hélice contínua, 3 – estacas escavadas)
Gráfico para determinar wbase,d,2 (1 – estacas cravadas, 2 – estacas de hélice contínua, 3 – estacas escavadas)
Cálculo da Curva Carga-Assentamento
Um dos resultados produzidos pelo programa é o diagrama de carregamento de uma estaca carregada verticalmente – curva carga-assentamento, que mostra o assentamento vertical em função do carga aplicada.
A curva carga-assentamento é determinada como o somatório dos assentamentos devido a forças na base da estaca e no furo, com base nos gráficos utilizados para calcular o assentamento da estaca. A figura seguinte mostra um exemplo de uma curva carga-assentamento.
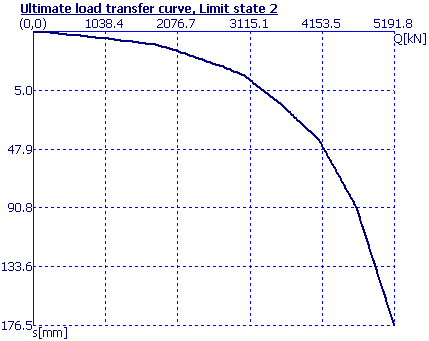 Curva carga-assentamento
Curva carga-assentamento
Verificação
A verificação capacidade de suporte de uma estaca (ou grupo de estacas) depende da metodologia de verificação selecionada na secção “Estaca via CPT”:
![]() verificação de acordo com EN 1997-2
verificação de acordo com EN 1997-2![]() verificação de acordo com o fator de segurança ou com a teoria dos estados limite
verificação de acordo com o fator de segurança ou com a teoria dos estados limite![]() verificação de acordo com NEN 6743
verificação de acordo com NEN 6743
No cálculo do assentamento é possível utilizar a curva carga-assentamento ou a curva carga-deslocamento, quando a Norma NEN 6743 é adotada.
Verificação de acordo com EN 1997-2
O programa determina as capacidades de suporte da base e do furo. O resultado são n valores para a capacidade de suporte total, para n CPTs:
![]()
![]()
| onde: | Rc,i | – | capacidade de suporte do iésimo CPT |
| Rcd,i | – | capacidade de suporte de dimensionamento do iésimo CPT | |
| Rb,i | – | capacidade de suporte da base do iésimo CPT | |
| Rs,i | – | capacidade de suporte do furo do iésimo CPT | |
| γb | – | fator parcial da resistência na base (definido na secção “Estaca via CPT”) | |
| γs | – | fator parcial da resistência no furo (definido na secção “Estaca via CPT”) |
A capacidade de suporte total é determinada a partir de:
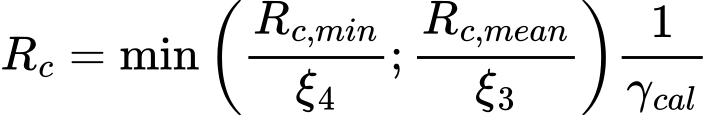 x
x
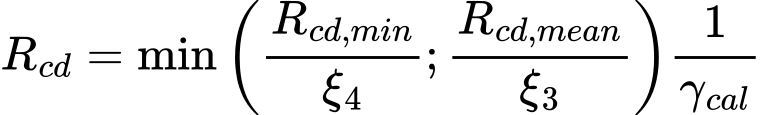
| onde: | Rc, min | – | capacidade de suporte mínima |
| Rc, mean | – | capacidade de suporte média de todos os CPTs |
O fator parcial do modelo de incerteza γcal é definido na janela “Configurações” (valor de origem é 1).
Os coeficientes de correlação ξ3 e ξ4 são definidos automaticamente, de acordo com o número de CPTs, ou definidos na janela “Configurações”. Para construções com rigidez suficiente e resistência, os coeficientes de correlação pode ser reduzidos pelo valor 1.1 (o resultado não pode ser inferior a 1.0).
A verificação da estaca é realizada através da seguinte equação:
![]()
| onde: | Fs,d | – | carga de dimensionamento |
| Rc,d | – | capacidade de suporte de dimensionamento da estaca |
Coeficientes de Correlação para Avaliar a Capacidade de Suporte de Estacas a partir de CPTs
Coeficientes de correlação ξ para avaliar a capacidade de suporte a partir de ensaios CPT (n – número de CPTs)
| ξ para n = | 1 | 2 | 3 | 4 | 5 | 7 | 10 |
| ξ3 | 1.40 | 1.35 | 1.33 | 1.31 | 1.29 | 1.27 | 1.25 |
| ξ4 | 1.40 | 1.27 | 1.23 | 1.20 | 1.15 | 1.12 | 1.08 |
Para a Norma NBN EN 1997-1 ABN, os coeficientes de correlação são considerados de acordo com a densidade dos CPTs no local de construção.
O coeficiente ξ3 é considerado de acordo com o seguinte:
| Número de Estacas | Densidade CPT | ||||
| 1 CPT por 10 m2 | 1 CPT por 50 m2 | 1 CPT por 100 m2 | 1 CPT por 300 m2 | 1 CPT por 1000 m2 | |
| 1-3 | 1,25 | 1,29 | 1,32 | 1,36 | 1,40 |
| 4-10 | 1,15 | 1,19 | 1,21 | 1,25 | 1,29 |
| > 10 | 1,14 | 1,17 | 1,20 | 1,24 | 1,27 |
O coeficiente ξ4 é considerado de acordo com o seguinte:
| Número de Estacas | Densidade CPT | ||||
| 1 CPT por 10 m2 | 1 CPT por 50 m2 | 1 CPT por 100 m2 | 1 CPT por 300 m2 | 1 CPT por 1000 m2 | |
| 1-3 | 1,08 | 1,17 | 1,23 | 1,31 | 1,40 |
| 4-10 | 1,00 | 1,07 | 1,13 | 1,21 | 1,29 |
| > 10 | 1,00 | 1,06 | 1,12 | 1,20 | 1,27 |
Verificação de acordo com o Fator de Segurança
A análise de verificação de acordo com o fator de segurança é selecionada na secção “Estaca via CPT”. Esta janela também permite definir o fator de segurança pretendido para a capacidade de suporte. A verificação da estaca é realizada através da expressão seguinte:
![]()
| onde: | Fs,d | – | carga na estaca |
| SFb | – | fator de segurança para a capacidade de suporte | |
| Fr,d | – | capacidade de suporte da estaca |
Verificação de acordo com os Estados Limite
A verificação de acordo com os estados limite é selecionada na secção “Estaca via CPT”, onde também é definido o coeficiente de redução da capacidade de suporte da estaca. Ao utilizar a Norma NEN 6743, o programa realiza a análise de verificação automaticamente, conforme especificado por esta norma, sendo que não é possível aceder à janela “Configurações“. A verificação da estaca para o primeiro estado limite é dado pela fórmula seguinte:
![]()
| onde: | Fs,d | – | carga de dimensionamento da estaca |
| γt | – | coeficiente de redução da capacidade de suporte | |
| Fr,d | – | capacidade de suporte de dimensionamento da estaca |
Análises através de SPTs
A capacidade de suporte da estaca é calculada com base em ensaios de penetração (SPTs) e no pefil do solo.
O método de cálculo é selecionado na janela “Configurações”:
![]() Décourt-Quaresma
Décourt-Quaresma
![]() Aoki-Velloso
Aoki-Velloso
Método Décourt-Quaresma
A resistência total da estaca é dada por:
![]()
| onde: | Rc | – | resistência total da estaca |
| Rb | – | resistência da base da estaca | |
| Rs | – | resistência do poço da estaca |
A resistência da base da estaca é dada por:
![]()
| onde: | α | – | coeficiente da base da estaca |
| Kdq | – | parâmetro do solo | |
| N | – | número médio de pancadas SPT ao nível da base da estaca | |
| Ab | – | área da base |
A resistência do poço da estaca é dada por:
![]()
| onde: | βi | – | coeficiente do poço da estaca na iésima camada |
| Ni | – | número médio de pancadas SPT na iésima camada | |
| As,i | – | área da base na iésima camada |
Bibliografia:
Cintra J.C.A., Aoki N. : Fundações por Estacas Projeto Geotécnico, Oficina de Textos, 2010, ISBN 978-85-7975-004-5
Parâmetro do Solo Kdq
O valor do parâmetro Kdq é automaticamente calculado de acordo com o tipo de solo, ou pode ser definido manualmente pelo usuário.
Tabela do parâmetro Kdq
| Tipo de Solo | Kdq [kPa] |
| Areia | 400 |
| Areia argilosa | 400 |
| Areia argiloso-siltosa | 400 |
| Areia silto-argilosa | 400 |
| Areia siltosa | 400 |
| Argila | 120 |
| Argila arenosa | 120 |
| Argila arenoso-siltosa | 120 |
| Argila silto-arenosa | 120 |
| Argila siltosa | 120 |
| Silte | 200 |
| Silte arenoso-siltoso | 250 |
| Silte arenoso | 250 |
| Silte argiloso-arenoso | 200 |
| Silte argiloso | 200 |
Coeficientes de Resistência α e β
O coeficiente da base da estaca α depende do tipo de estaca. Os valores podem ser inseridos manualmente pelo usuário ou calculados automaticamente de acordo com o tipo de estaca e de solo.
| Estacas | α para areia | α para argila | α para silte |
| Estacas cravadas prefabricadas ou em aço | 1.0 | 1.0 | 1.0 |
| Estacas Franki | 1.0 | 1.0 | 1.0 |
| Estacas cravadas em madeira | 1.0 | 1.0 | 1.0 |
| Estacas vibradas ou vibro-comprimidas | 1.0 | 1.0 | 1.0 |
| Estacas enroscadas realizadas no local | 1.0 | 1.0 | 1.0 |
| Estacas enroscadas prefabricadas | 1.0 | 1.0 | 1.0 |
| Estacas enroscadas realizadas no local com argamassa adicional | 1.0 | 1.0 | 1.0 |
| Estacas enroscadas prefabricadas com argamassa adicional | 1.0 | 1.0 | 1.0 |
| Estacas tubulares em aço | 1.0 | 1.0 | 1.0 |
| Estacas Continuous Flight Auger (CFA) | 0.3 | 0.3 | 0.3 |
| Estacas escavadas ou em cortina em suspensão de bentonite | 0.5 | 0.85 | 0.6 |
| Estacas escavadas com revestimento metálico | 0.5 | 0.85 | 0.6 |
| Estacas raiz | 0.5 | 0.85 | 0.6 |
| Estacas Strauss | 0.5 | 0.85 | 0.6 |
O coeficiente do poço da estaca β é determinado automaticamente de acordo com o tipo de solo e de estaca, ou pode ser definido manualmente pelo usuário.
| Estacas | β para areia | β para argila | β para silte |
| Estacas cravadas prefabricadas ou em aço | 1.0 | 1.0 | 1.0 |
| Estacas Franki | 1.0 | 1.0 | 1.0 |
| Estacas cravadas em madeira | 1.0 | 1.0 | 1.0 |
| Estacas vibradas ou vibro-comprimidas | 1.0 | 1.0 | 1.0 |
| Estacas enroscadas realizadas no local | 1.0 | 1.0 | 1.0 |
| Estacas enroscadas prefabricadas | 1.0 | 1.0 | 1.0 |
| Estacas enroscadas realizadas no local com argamassa adicional | 1.0 | 1.0 | 1.0 |
| Estacas enroscadas prefabricadas com argamassa adicional | 1.0 | 1.0 | 1.0 |
| Estacas tubulares em aço | 1.0 | 1.0 | 1.0 |
| Estacas Continuous Flight Auger (CFA) | 1.0 | 1.0 | 1.0 |
| Estacas escavadas ou em cortina em suspensão de bentonite | 0.6 | 0.9 | 0.75 |
| Estacas escavadas com revestimento metálico | 0.5 | 0.8 | 0.65 |
| Estacas raiz | 1.5 | 1.5 | 1.5 |
| Estacas Strauss | 0.5 | 0.8 | 0.65 |
Método Aoki-Velloso
A resistência total da estaca é dada por:
![]()
| onde: | Rc | – | resistência total da estaca |
| Rb | – | resistência da base da estaca | |
| Rs | – | resistência do poço da estaca |
A resistência da base da estaca é dada por:
![]()
| onde: | Kav | – | parâmetro do solo |
| N | – | número médio de pancadas SPT ao nível da base da estaca | |
| F1 | – | coeficiente de tecnologia na base da estaca | |
| Ab | – | área da base |
A resistência do poço da estaca é dada por:
![]()
| onde: | αi | – | parâmetro de resistência no poço da estaca ma iésima camada |
| Kav,i | – | parâmetro do solo na iésima camada | |
| Ni | – | número médio de pancadas SPT ao nível da base da estaca | |
| F2 | – | coeficiente de tecnologia na base da estaca | |
| As,i | – | área da base na iésima camada |
Bibliografia:
Cintra J.C.A., Aoki N. : Fundações por Estacas Projeto Geotécnico, Oficina de Textos, 2010, ISBN 978-85-7975-004-5.
Parâmetros do Solo Kav e α
O valores dos parâmetros Kav e α são automaticamente calculados de acordo com o tipo de solo, ou podem ser definidos manualmente pelo usuário.
Tabela dos parâmetros Kav e α
| Tipo de Solo | Kav [kPa] | α [%] |
| Areia | 1000 | 1,4 |
| Areia argilosa | 600 | 3,0 |
| Areia argiloso-siltosa | 500 | 2,8 |
| Areia silto-argilosa | 700 | 2,4 |
| Areia siltosa | 800 | 2,0 |
| Argila | 200 | 6,0 |
| Argila arenosa | 350 | 2,4 |
| Argila arenoso-siltosa | 300 | 2,8 |
| Argila silto-arenosa | 330 | 3,0 |
| Argila siltosa | 220 | 4,0 |
| Silte | 400 | 3,0 |
| Silte arenoso-siltoso | 450 | 2,8 |
| Silte arenoso | 550 | 2,2 |
| Silte argiloso-arenoso | 250 | 3,0 |
| Silte argiloso | 230 | 3,4 |
Coeficientes de Tecnologia da Estaca
O coeficiente F1 reduz a resistência da base da estaca e o coeficiente F2 reduz a resistência do poço da estaca. Os valores podem ser inseridos manualmente pelo usuário ou calculados automaticamente de acordo com o tipo de estaca através da tabela seguinte:
| Estacas | F1 | F2 |
| Estacas cravadas prefabricadas ou em aço | 1.2 | 2.3 |
| Estacas Franki | 2.3 | 3.0 |
| Estacas cravadas em madeira | 5.0 | 5.0 |
| Estacas vibradas ou vibro-comprimidas | 2.3 | 3.2 |
| Estacas enroscadas realizadas no local | 3.0 | 4.0 |
| Estacas enroscadas prefabricadas | 2.5 | 4.0 |
| Estacas enroscadas realizadas no local com argamassa adicional | 3.0 | 3.5 |
| Estacas enroscadas prefabricadas com argamassa adicional | 2.5 | 3.5 |
| Estacas tubulares em aço | 1.8 | 3.5 |
| Estacas Continuous Flight Auger (CFA) | 3.0 | 3.8 |
| Estacas escavadas ou em cortina em suspensão de bentonite | 3.5 | 7.0 |
| Estacas escavadas com revestimento metálico | 4.0 | 3.9 |
| Estacas raiz | 2.2 | 2.4 |
| Estacas Strauss | 4.2 | 3.9 |
Sapata via CPT/SPT
Este programa é utilizado para o dimensionamento e verificação de sapatas de fundação, com base em resultados obtidos a partir de ensaios de campo (CPT, SPT, PMT).
O programa realiza análises para:
![]() capacidade de suporte vertical
capacidade de suporte vertical
![]() capacidade de suporte horizontal
capacidade de suporte horizontal
![]() assentamento
assentamento
![]() armadura longitudinal e transversal (punçoamento)
armadura longitudinal e transversal (punçoamento)
Análise da Capacidade de Carga
A capacidade de suporte do solo de fundação pode ser calculada de acordo com ensaios CPT, SPT, ou PMT e verificada de acordo com o fator de segurança:
![]()
| onde: | σ | – | tensão de contacto extremo na base da sapata |
| Rd | – | capacidade de carga do solo de fundação | |
| SFv | – | fator de segurança para a capacidade de suporte vertical (a inserir na janela “Análises”) |
A tensão de contacto extremo de dimensionamento na base da sapata é dada por:
![]()
| onde: | V | – | força vertical extrema |
| Aef | – | área efetiva da fundação |
Capacidade de suporte Rd determinada a partir de ensaios CPT:
![]() Método de “Meyerhof”
Método de “Meyerhof”
![]() Método de “Schmertmann”
Método de “Schmertmann”
![]() Método de “Skempton”
Método de “Skempton”
Capacidade de suporte Rd determinada a partir de ensaios SPT:
![]() Método de “Meyerhof”
Método de “Meyerhof”
Capacidade de suporte Rd determinada a partir de ensaios PMT:
![]() “NF P94-261”
“NF P94-261”
Método de Meyerhof (CPT)
Este método para solos não coesivos utiliza a teoria de Meyerhof, em que a capacidade de suporte do solo de fundação é dado pela fórmula seguinte:
![]()
É recomendável utilizar um fator de segurança FS = 3 ao calcular a capacidade de suporte através deste método.
| onde: | Rd | – | capacidade de suporte do solo de fundação |
| qc | – | valor médio da resistência de penetração de cone medida entre a profundidade da base da sapata e 1,5*bef abaixo da base da sapata | |
| bef | – | largura efetiva da sapata | |
| Cw1,Cw2 | – | fatores da influência do nível freático | |
| d | – | profundidade da base da sapata | |
| Ri | – | fator de inclinação da carga |
A formula utiliza unidades no sistema imperial [tsf, ft] – o programa calcula automaticamente os valores com as unidades definidas.
Os fatores de influência do nível freático Cw1 e Cw2 são determinados da seguinte forma:
hGWT = 0 (nível freático ao nível do terreno) -> Cw1 = Cw2 = 0,5
hGWT = d (nível freático ao nível da base da sapata) -> Cw1 = 0,5; Cw2 = 1
hGWT > d + 1,5*bef -> Cw1 = Cw2 = 1
| onde: | hGWT | – | profundidade do nível freático medido a partir da superfície do terreno |
Os valores intermédios de Cw1 e Cw2 são interpolados.
A fator de inclinação de carga Ri é interpolado de acordo com a tabela seguinte:
| H/V | Ri | ||
| d/bef = 0 | d/bef = 1 | d/bef = 5 | |
| 0,10 | 0,75 | 0,8 | 0,85 |
| 0,15 | 0,65 | 0,75 | 0,80 |
| 0,20 | 0,55 | 0,65 | 0,70 |
| 0,25 | 0,50 | 0,55 | 0,65 |
| 0,30 | 0,40 | 0,50 | 0,55 |
| 0,35 | 0,35 | 0,45 | 0,50 |
| 0,40 | 0,30 | 0,35 | 0,45 |
| 0,45 | 0,25 | 0,30 | 0,40 |
| 0,50 | 0,20 | 0,25 | 0,30 |
| 0,55 | 0,15 | 0,20 | 0,25 |
| 0,60 | 0,10 | 0,15 | 0,20 |
| onde: | H | – | componente horizontal da carga resultante |
| V | – | componente vertical da carga resultante |
Este método não deve ser aplicada para um rácio de H/V > 0,6.
A influência da superfície do terreno inclinada e da base da fundação inclinada é considerada da mesma forma que no método de Schmertmann.
Bibliografia:
FHWA-SA-91-043: THE CONE PENETROMETER TEST
Bridge Engineering Handbook (Wai-Fah Chen, Lian Duan, 1999)
Método de Schmertmann (CPT)
Este método para solos não coesivos utiliza a teoria de Schmertmann, em que a capacidade de suporte do solo de fundação é dado pela fórmula seguinte:
![]()
É recomendável utilizar um fator de segurança FS = 3 ao calcular a capacidade de suporte através deste método.
| onde: | Rd | – | capacidade de suporte do solo de fundação |
| Kq, Kγ | – | fatores de redução | |
| γ | – | peso volúmico do solo na base da sapata | |
| bef | – | largura efetiva da sapata | |
| Nq, Nγ | – | fatores da capacidade de suporte | |
| d | – | profundidade da base da sapata |
A formula utiliza unidades no sistema imperial [tsf, tcf, ft] – o programa calcula automaticamente os valores com as unidades definidas.
![]()
| onde: | qc1 | – | valor médio da resistência de penetração de cone medida entre a profundidade da base da sapata e 0,5*bef abaixo da base da sapata |
| qc2 | – | valor médio da resistência de penetração de cone medida entre 0,5*bef abaixo da base da sapata e 1,5*bef abaixo da base da sapata |
![]()
![]()
| onde: | iq, iγ | – | fatores de inclinação da carga |
| sq, sγ | – | fatores da forma da sapata | |
| dq | – | fator da profundidade da sapata | |
| bq, bγ | – | fatores da inclinação da base da sapata | |
| gq, gγ | – | fatores da inclinação do solo |
Os fatores de inclinação iq e iγ são determinados através de:
![]()
![]()
![]()
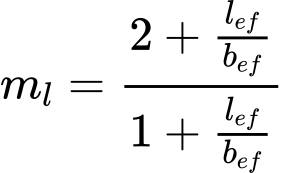
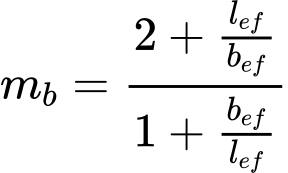
| onde: | H | – | componente horizontal da carga resultante |
| V | – | componente vertical da carga resultante | |
| lef | – | comprimento efetivo da sapata | |
| θ | – | ângulo entre a componente horizontal da carga resultante H e o eixo maior da sapata (na direção de lef) |
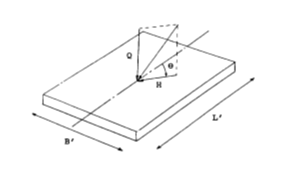 Determinação do ângulo θ
Determinação do ângulo θ
Este método não deve ser aplicada para um rácio de H/V > 0,4.
Os fatores de forma sq e sγ são determinados através de:
![]()
![]()
| onde: | φ | – | ângulo de atrito interno na base da sapata |
O fator da profundidade da base da sapata dq é determinado através de:
![]()
Os fatores de inclinação da base da sapata bq e bγ são determinados através de:
![]()
| onde: | η | – | ângulo de inclinação da base da sapata |
Os fatores de inclinação do solo gq e gγ são determinados através de:
![]()
| onde: | β | – | ângulo de inclinação do solo |
Bibliografia:
FHWA-SA-91-043: THE CONE PENETROMETER TEST
Bridge Engineering Handbook (Wai-Fah Chen, Lian Duan, 1999)
Método de Skempton (CPT)
Este método para solos coesivos utiliza a teoria de Skempton, em que a capacidade de suporte do solo de fundação é dado pela fórmula seguinte:
![]()
É recomendável utilizar um fator de segurança FS = 3 ao calcular a capacidade de suporte através deste método.
| onde: | Rd | – | capacidade de suporte do solo de fundação |
| Kc | – | fator de inclinação da carga | |
| Nc | – | fator da capacidade de carga de Skempton | |
| Su | – | resistência ao cisalhamento não drenada | |
| γ | – | peso volúmico do solo na base da sapata | |
| d | – | profundidade da base da sapata |
A formula utiliza unidades no sistema imperial [tsf, tcf, ft] – o programa calcula automaticamente os valores com as unidades definidas.
![]()
| onde: | H | – | componente horizontal da carga resultante |
| V | – | componente vertical da carga resultante |
Este método não deve ser aplicada para um rácio de H/V > 0,4.
O fator da capacidade de suporte de Skempton Nc depende do rácio entre a largura efetiva bef e o comprimento efetivo lef e do rácio entre a profundidade da base da sapata d e a largura efetiva bef.
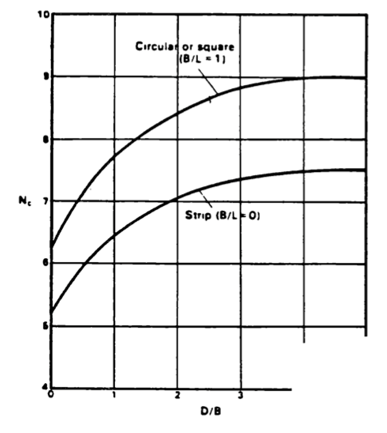 Determinação do fator Nc (fonte: Peck, Hanson e Thornburn, 1974)
Determinação do fator Nc (fonte: Peck, Hanson e Thornburn, 1974)
A resistência ao cisalhamento não drenada Su é determinada através de:
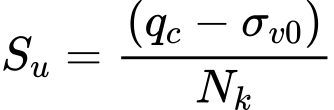
| onde: | qc | – | valor médio da resistência da penetração de cone |
| σv0 | – | valor médio da tensão vertical medida entre a profundidade da base da sapata e 1,5*bef abaixo da base da sapata | |
| Nk | – | fator do cone (intervalo <10;20>) |
![]()
| onde: | qc1 | – | valor médio da resistência de penetração de cone medida entre a profundidade da base da sapata e 0,5*bef abaixo da base da sapata |
| qc2 | – | valor médio da resistência de penetração de cone medida entre 0,5*bef abaixo da base da sapata e 1,5*bef abaixo da base da sapata |
A influência da superfície do terreno inclinada e da base da fundação inclinada é considerada da mesma forma que no método de Schmertmann.
Bibliografia:
FHWA-SA-91-043: THE CONE PENETROMETER TEST
Bridge Engineering Handbook (Wai-Fah Chen, Lian Duan, 1999)
Método de Meyerhof (SPT)
Este método para solos coesivos e não coesivos utiliza a teoria de Meyerhof, em que a capacidade de suporte do solo de fundação é dado pela fórmula seguinte:
![]()
É recomendável utilizar um fator de segurança FS = 3 ao calcular a capacidade de suporte através deste método.
| onde: | Rd | – | capacidade de suporte do solo de fundação |
| N | – | valor médio do número de pancadas SPT medidas entre a profundidade da base da sapata e 1,5*bef abaixo da base da sapata | |
| bef | – | largura efetiva da sapata | |
| Cw1,Cw2 | – | fatores da influência do nível freático | |
| d | – | profundidade da base da sapata | |
| Ri | – | fator de inclinação da carga |
A formula utiliza unidades no sistema imperial [tsf, ft] – o programa calcula automaticamente os valores com as unidades definidas.
Em solos saturados muito finos ou em areias siltosas, o número de pancadas SPT para Ni > 15, deve ser corrigido da seguinte forma:
![]()
Esta correlação pode ser realizada automaticamente na janela “Análises”.
Os fatores de influência do nível freático Cw1 e Cw2 são determinados da seguinte forma:
hGWT = 0 (nível freático ao nível do terreno) -> Cw1 = Cw2 = 0,5
hGWT = d (nível freático ao nível da base da sapata) -> Cw1 = 0,5; Cw2 = 1
hGWT > d + 1,5*bef -> Cw1 = Cw2 = 1
| onde: | hGWT | – | profundidade do nível freático medido a partir da superfície do terreno |
Os valores intermédios de Cw1 e Cw2 são interpolados.
A fator de inclinação de carga Ri é interpolado de acordo com a tabela seguinte:
| H/V | Ri | ||
| d/bef = 0 | d/bef = 1 | d/bef = 5 | |
| 0,10 | 0,75 | 0,8 | 0,85 |
| 0,15 | 0,65 | 0,75 | 0,80 |
| 0,20 | 0,55 | 0,65 | 0,70 |
| 0,25 | 0,50 | 0,55 | 0,65 |
| 0,30 | 0,40 | 0,50 | 0,55 |
| 0,35 | 0,35 | 0,45 | 0,50 |
| 0,40 | 0,30 | 0,35 | 0,45 |
| 0,45 | 0,25 | 0,30 | 0,40 |
| 0,50 | 0,20 | 0,25 | 0,30 |
| 0,55 | 0,15 | 0,20 | 0,25 |
| 0,60 | 0,10 | 0,15 | 0,20 |
| onde: | H | – | componente horizontal da carga resultante |
| V | – | componente vertical da carga resultante |
Este método não deve ser aplicada para um rácio de H/V > 0,6.
A influência da superfície do terreno inclinada e da base da fundação inclinada é considerada da mesma forma que no método de Schmertmann.
Bibliografia:
Bridge Engineering Handbook (Wai-Fah Chen, Lian Duan, 1999)
NF P94-261 (PMT)
Esta solução para solos coesivos e não coesivos baseia-se na teoria formulada na Norma Francesa NF P94-261, em que a capacidade de carga do solo de fundação é dada pela fórmula:
![]()
É recomendável utilizar um fator de segurança FS = 3 ao calcular a capacidade de carga através deste método.
| Onde: | Rd | – | capacidade de carga do solo de fundação |
| p*le | – | pressão equivalente líquida limite | |
| kp | – | fator de capacidade da carga | |
| iδ | – | fator de inclinação da carga | |
| ig | – | fator de inclinação do solo |
A pressão equivalente líquida limite ple* é a media geométrica dos valores da pressão limite pressiométrica desde a base da sapata até à profundidade hr.
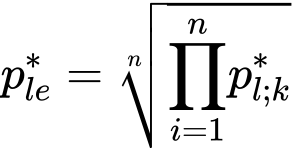
A profundidade hr depende do tipo de carga (dimensionamento/serviço), geometria da fundação e excentricidade da carga:
| carga de dimensionamento | carga de serviço | ||
| Sapata contínua |
| ||
| Sapata circular | |||
| Sapata retangular | |||
O fator de capacidade da carga kp depende do tipo de solo, geometria da fundação (rácio L/B) e profundidade embutida equivalente De.
A profundidade embutida equivalente De é calculada através de:
![]()
ou:
![]()
Os valores de pLM,i utilizados para determinar a profundidade embutida equivalente De são medidos entre a superfície do terreno e a base da fundação.
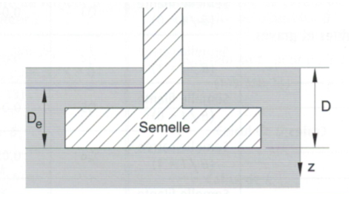
Se De/B < 2 :
![]()
Cálculo de kp para fundações contínuas, circulares ou retangulares:
![]()
Cálculo de kp para sapatas isoladas (rácio L/B)
![]()
Os coeficientes a, b, c, kp0 e kpmax dependem do tipo de solo, de acordo com a tabela seguinte:
| Categoria do solo | Curva de variação do fator de carga | Expressão de kp | |||||
| a | b | c | kp0 (De/B=0) | kpmax | |||
| Argilas & Siltes | Sapata contínua (B/L = 0) | Q1 | 0.20 | 0.02 | 1.30 | 0.80 | 1.022 |
| Sapata retangular (B/L = 1) | Q2 | 0.30 | 0.02 | 1.50 | 0.80 | 1.123 | |
| Areia & Cascalho | Sapata contínua (B/L = 0) | Q3 | 0.30 | 0.05 | 2.00 | 1.00 | 1.393 |
| Sapata retangular (B/L = 1) | Q4 | 0.22 | 0.18 | 5.00 | 1.00 | 1.580 | |
| Giz | Sapata contínua (B/L = 0) | Q5 | 0.28 | 0.22 | 2.80 | 0.80 | 1.517 |
| Sapata retangular (B/L = 1) | Q6 | 0.35 | 0.31 | 3.00 | 0.80 | 1.768 | |
| Margas & Calcários | Sapata contínua (B/L = 0) | Q7 | 0.20 | 0.20 | 3.00 | 0.80 | 1.399 |
| Sapata retangular (B/L = 1) | Q8 | 0.20 | 0.30 | 3.00 | 0.80 | 1.598 | |
O fator de inclinação da carga iδ é calculado através de:
![]()
Se δd < π/4:
![]()
Se δd ≥ π/4:
![]()
Bibliografia:
NF P94-261
Capacidade de Carga Horizontal
A capacidade de carga horizontal da fundação é verificada de acordo com o fator de segurança:
![]()
onde Rdh depende do tipo de subsolo (selecionado na janela “Configurações”):
![]() Análise para condições drenadas:
Análise para condições drenadas:
![]()
![]() Análise para condições não drenadas:
Análise para condições não drenadas:
![]()
e:
![]()
| onde: | ψ | – | ângulo de atrito entre a fundação e o solo |
| a | – | coesão entre a fundação e o solo | |
| Aef | – | área efetiva da fundação | |
| Hx,Hy | – | componentes horizontais da força | |
| Q | – | força vertical extrema de dimensionamento | |
| SF | – | fator de segurança para a capacidade de carga horizontal (definido na janela “Análise”) |
O ângulo de atrito entre a fundação e o solo ψ recomendado é:
![]() Para fundações realizadas no local:
Para fundações realizadas no local:
![]()
![]() Para fundações prefabricadas:
Para fundações prefabricadas:
![]()
| onde: | φ | – | ângulo de atrito entre o solo e a base da fundação |
Bibliografia:
NF P94-261
Análise de Assentamento
O assentamento de uma sapata de fundação pode ser calculado de acordo com ensaios CPT, SPT, ou PMT.
Assentamento determinado a partir de ensaios CPT:
![]() Método de “Schmertmann”
Método de “Schmertmann”
Assentamento determinado a partir de ensaios SPT:
![]() Método de “NAVFAC DM7”
Método de “NAVFAC DM7”
Assentamento determinado a partir de ensaios PMT:
![]() “NF P94-261”
“NF P94-261”
Método de Schmertmann (CPT)
O assentamento de sapatas de fundação com base em ensaios CPT, de acordo com a teoria de Schmertmann, é dado pela fórmula seguinte:
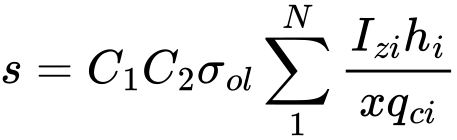
| onde: | s | – | assentamento da sapata |
| C1 | – | fator de correção da profundidade da sapata | |
| C2 | – | fator de correção para assentamento por fluência | |
| σol | – | tensão na base da sapata | |
| Izi | – | fator de influência da deformação no centro da iésima subcamada | |
| hi | – | espessura da iésima subcamada | |
| χ | – | fator do módulo | |
| qci | – | valor médio da resistência de penetração de cone da iésima subcamada |
A formula utiliza unidades no sistema imperial [tsf, ft] – o programa calcula automaticamente os valores com as unidades definidas.
O fator de correção da profundidade da sapata C1 é determinado através de:
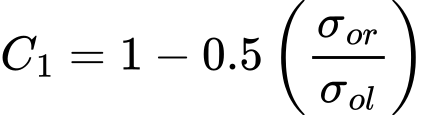
| onde: | σor | – | tensão geostática na base da sapata |
O fator de correção de assentamento por fluência C2 é determinado através de:
![]()
| onde: | tyr | – | tempo, em anos, após a aplicação da carga |
O fator do módulo χ depende do rácio entre o comprimento l e a largura b da sapata:
l/b = 1 -> χ = 2,5
l/b = 10 -> χ = 3,5
Os valores intermédios de χ são interpolados.
O eixo horizontal do gráfico representa o fator de influência da deformação Iz. O eixo vertical representa a profundidade abaixo da base da sapata.
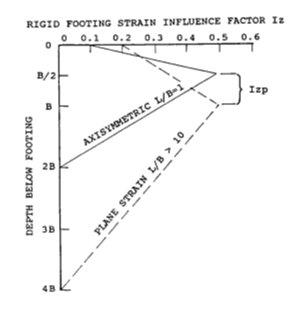 Determinação do fator Iz (Schmertmann, 1978)
Determinação do fator Iz (Schmertmann, 1978)
O diagrama para o fator Iz também depende do rácio entre o comprimento l e a largura b da sapata.
Para o rácio l/b = 1, o valor máximo do fator de influência da deformação Izp verifica-se para a profundidade b/2 abaixo da base da fundação e o assentamento total é calculado para a profundidade 2b abaixo da base da fundação.
Para o rácio l/b = 10, o valor máximo do fator de influência da deformação Izp verifica-se para a profundidade b abaixo da base da fundação e o assentamento total é calculado para a profundidade 4b abaixo da base da fundação.
O valor máximo da influência de deformação Izp é determinado a partir de:
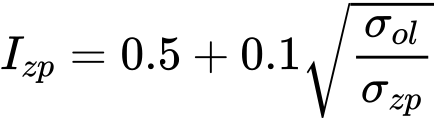
| onde: | σzp | – | tensão geostática à profundidade b/2 (para o rácio l/b = 1) ou b (l/b = 10) abaixo da base da fundação |
O fator de influência de deformação Iz é interpolado para valores intermédios do rácio l/b (1 < l/b < 10).
Bibliografia:
Schmertmann, J.H. (1970). Static cone to compute static settlement over sand. ASCE Journal of SoilMechanics & Foundations Division, 96 (3), 1011-1043.
Schmertmann, J.H., Hartmann, J.P. and Brown, P.R. (1978). Improved strain influence factor diagrams,ASCE Journal of the Geotechnical Engineering Division, 104 (GT8), 113
Método NAVFAC DM7 (SPT)
O assentamento de sapatas de fundação com base em sondagens SPT, de acordo com o método NAVFAC DM7, é dado pela fórmula seguinte:
![]()
| onde: | s | – | assentamento da sapata |
| C | – | fator da largura da sapata | |
| σ | – | tensão na base da sapata | |
| Kv | – | módulo de reação da superfície | |
| b | – | largura da sapata | |
| Cw | – | fator de influência do nível freático |
A formula utiliza unidades no sistema imperial [tsf, tcf, ft] – o programa calcula automaticamente os valores com as unidades definidas.
O fator de largura da sapata C é determinado a partir de:
b < 20 ft -> C = 4
b > 40 ft -> C = 2
Os valores intermédios de C são interpolados.
O fator de influência do nível freático Cw é determinado a partir de:
Se o nível freático se localizar entre a superfície do terreno e a profundidade de 1,5*bef abaixo da base da sapata:
![]()
![]()
Se o nível freático se localizar abaixo da profundidade de 1,5*bef abaixo da base da sapata:
![]()
| onde: | hGWT | – | profundidade do nível freático a partir da superfície do terreno |
| d | – | profundidade da base da sapata |
O módulo de reação da superfície Kv depende do fator de densidade relativa ID:
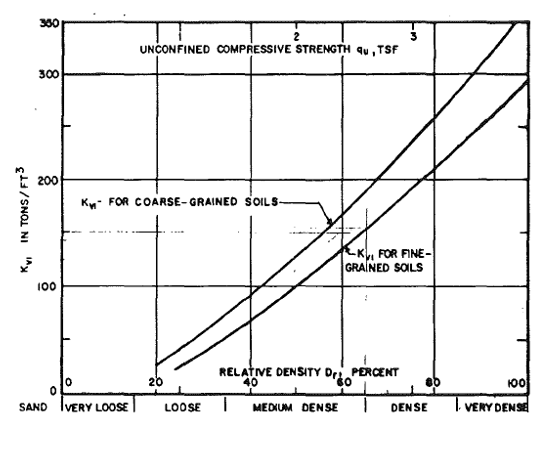 Determinação do módulo Kv (Navfac, 1982)
Determinação do módulo Kv (Navfac, 1982)
O fator de densidade relativa ID é determinado a partir de:
σzp ≤ 1,5 [ksf]:
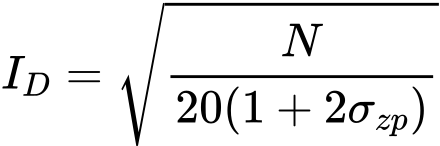
σzp > 1,5 [ksf]:
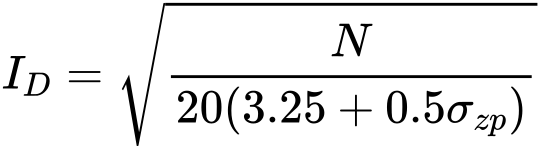
| onde: | N | – | número de pancadas não corrigido para a profundidade de b/2 abaixo da base da sapata |
| σzp | – | tensão geostática à profundidade de b/2 abaixo da base da sapata |
A formula utiliza unidades no sistema imperial [ksf] – o programa calcula automaticamente os valores com as unidades definidas.
Bibliografia:
Navfac, 1982
NF P94-261 (PMT)
O assentamento de uma sapata através de PMTs, de acordo com o método NF P94-261, baseia-se na fórmula seguinte:
![]()
| onde: | s | – | assentamento total |
| Ec, Ed | – | módulo pressiométrico equivalente | |
| α | – | coeficiente reológico | |
| q | – | tensão na base da sapata | |
| λc, λd | – | coeficientes de forma | |
| B | – | largura da sapata | |
| B0 | – | largura de referência (0,6 m) |
Valores aproximados do coeficiente reológico α de solos:
| Argila | Silte | Areia | Cascalho | |
| Sobreconsolidado | 1 | 2/3 | 1/2 | 1/3 |
| Normalmente consolidado | 2/3 | 1/2 | 1/3 | 1/4 |
| Não consolidado | 1/2 | 1/2 | 1/3 | 1/4 |
Valores aproximados do coeficiente reológico α para rochas:
| Rochas | |
| Tipo | α |
| Quase intacta | 2/3 |
| Normalmente fraturada | 1/2 |
| Muito fraturada | 1/3 |
| Muito alterada | 2/3 |
Os coeficientes de forma λc, λd são interpolados de acordo com a tabela seguinte:
| L/B | circular | quadrada | 2 | 3 | 5 | 20 |
| λd | 1 | 1,12 | 1,53 | 1,78 | 2,14 | 2,65 |
| λc | 1 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 |
Os módulos pressiométricos equivalentes Ec e Ed são determinados de acordo com o módulo pressiométrico medido nas camadas com espessura B/2 abaixo da base da fundação.

O módulo Ec é determinado como uma média do módulo pressiométrico na primeira camada com espessura B/2 abaixo da base da fundação.
![]()
A determinação do módulo Ed depende da profundidade total do PMT (dPMT).
![]()
![]()
![]()
![]()
![]()
![]()
Bibliografia:
CSN EN 1997-2 Annex E
NF P94-261
Menard, L. (1975): “The Menard Pressuremeter: Interpretation and Application of the Pressuremeter Test Results to Foundations Design”, Sols-Soils, No. 26, Paris, France.
Grupo de Estacas
As análises realizadas no programa “Grupo de Estacas” podem ser divididas em dois grupos:
![]() Solução analítica – cálculo da capacidade de suporte vertical de um grupo de estacas para solos coesivos e não coesivos e determinação do assentamento
Solução analítica – cálculo da capacidade de suporte vertical de um grupo de estacas para solos coesivos e não coesivos e determinação do assentamento
![]() Análise de um grupo de estacas através do método de mola, com a determinação da armadura das estacas
Análise de um grupo de estacas através do método de mola, com a determinação da armadura das estacas
Solução Analítica
A análise da capacidade de suporte vertical de um grupo de estacas pode ser realizada para:
![]() solos não coesivos (análise para condições drenadas)
solos não coesivos (análise para condições drenadas)
![]() solos coesivos (análise para condições não drenadas)
solos coesivos (análise para condições não drenadas)
A análise de verificação é executada de acordo com os fatores de segurança ou com a teoria dos estados limite.
A verificação é realizada apenas para a carga vertical. A carga devido a momentos e forças de cisalhamento não é considerada. Para considerar ações horizontais no grupo de estacas deve ser selecionada a opção método de mola na janela “Configurações”.
Os métodos analíticos também permitem calcular o assentamento do grupo de estacas.
Solo Não Coesivo (Análise para Condições Drenadas)
Para calcular a capacidade de suporte vertical de um grupo de estacas, são utilizados os mesmo métodos que na análise de uma estaca isolada:
![]() NAVFAC DM 7.2
NAVFAC DM 7.2
![]() Tensão efetiva
Tensão efetiva
![]() CSN 73 1002
CSN 73 1002
A capacidade vertical do grupo de estacas é dada por:
![]()
| onde: | n | – | número de estacas no grupo |
| Rc | – | capacidade de suporte vertical de uma estaca isolada | |
| ηg | – | eficiência do grupo de estacas |
A análise de verificação é realizada de acordo com os fatores de segurança ou com a teoria dos estados limite.
Eficiêncida de Um Grupo de Estacas
UFC 3-220-01A
![]()
![]() para uma distância axial entre estacas do grupo de: 3d
para uma distância axial entre estacas do grupo de: 3d
![]()
![]() para uma distância axial entre estacas do grupo de: 6d
para uma distância axial entre estacas do grupo de: 6d
La Barré (CSN 73 1002):
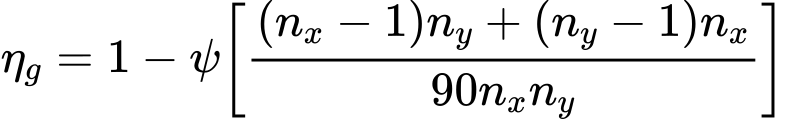
![]()
| onde: | nx | – | número de estacas na direção x |
| ny | – | número de estacas na direção y | |
| ψ | – | ângulo com tangente | |
| s | – | espaçamento axial entre estacas | |
| d | – | diâmetro das estacas |
Fórmula de Seiler-Keeney:
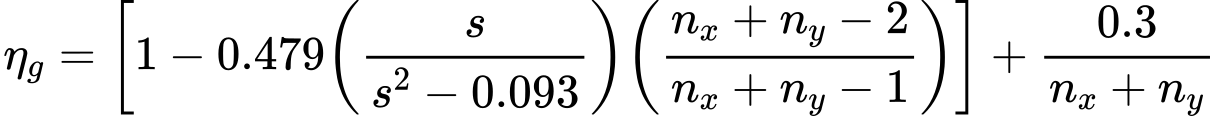
| onde: | nx | – | número de estacas na direção x |
| ny | – | número de estacas na direção y | |
| s | – | espaçamento axial entre estacas |
Inserir eficiência
O nível de eficiência pode ser definido pelo usuário, dentro do intervalo 0.5 – 1.0.
Bibliografia:
Pochman, R.; Simek, J.: Pilotove zaklady – Komentar k CSN 73 1002. 1st edition, Prague, Vydavatelstvi norem, 1989, 80 p.
Unified Facilities Criteria (UFC 3-220-01A): Design of deep foundations – Technical instructions, Chapter 5-3, 1997.
Venkatramaiah, C.: Geotechnical Engineering. Second edition, New Delhi (India): New Age International Publishers, 1995.
Solo Coesivo (Análise para Condições Não Drenadas)
UFC 3-220-01A:
A capacidade de suporte de um maciço de terra é dada por:
![]()
| onde: | 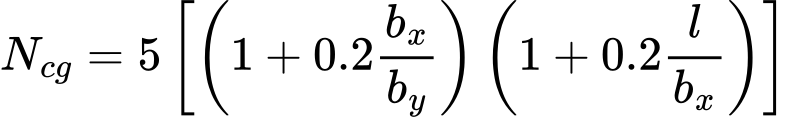 | para a condição: | |
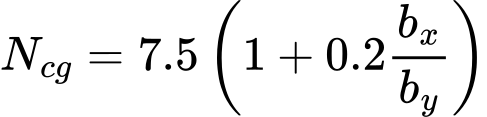 | para a condição: |
Masopust:
A capacidade de suporte de um maciço de terra é dada por:
![]()
![]()
| onde: | l | – | comprimento das estacas |
| bx,by | – | dimensões planas de um corpo de terra em forma de bloco | |
| cus | – | capacidade de suporte não drenada média ao longo das estacas ( | |
| cub | – | capacidade de suporte não drenada na base das estacas | |
| Ncg | – | fator da capacidade de suporte da coesão do grupo | |
| bx | – | largura mínima do grupo de estacas (lado menor do capeamento das estacas) |
Nota: O maciço de terra é representado por um bloco com a base definida por um plano que contém a base de cada estaca e com as paredes verticais à distância de um diâmetro de estaca medido a partir dos eixos das estacas exteriores. Este bloco de terra está sujeito a carregamentos globais causados pela resistência do grupo de estacas devido ao cisalhamento ao longo das paredes – atrito superficial e devido à capacidade de suporte na sua base.
A análise de verificação é realizada de acordo com os fatores de segurança ou com a teoria dos estados limite.
Bibliografia:
UFC 3-220-01A
MASOPUST, Jan. Navrhování základových a pažicích konstrukcí: příručka k ČSN EN 1997. Praha: Pro Českou komoru autorizovaných inženýrů a techniků činných ve výstavbě vydalo Informační centrum ČKAIT, 2012. ISBN 978-80-87438-31-2.
Análise de acordo com o Fator de Segurança
Ao executar a análise de acordo com o fator de segurança, o programa realiza a análise de verificação para um grupo de estacas à compressão:
![]()
| onde: | Rg | – | capacidade de suporte vertical de um grupo de estacas |
| Vd | – | força vertical máxima (incluindo o peso próprio do capeamento do grupo de estacas) | |
| Wp | – | peso próprio das estacas (apenas quando a opção “Considerar o peso próprio da estaca” estiver selecionado) | |
| SFcp | – | fator de segurança para um grupo de estacas à compressão |
Análise de acordo com a Teoria dos Estados Limite
Ao realizar a análise de acordo com a teoria dos estados limite, o programa executa a análise de verificação para um grupo de estacas em solo não coesivo:
![]()
| onde: | Rg | – | capacidade de suporte vertical de um grupo de estacas |
| n | – | número de estacas no grupo | |
| Rc | – | capacidade de suporte vertical de uma estaca isolada (Rb + Rs) | |
| γt | coeficiente de redução ca resistência global | ||
| ηg | – | eficiência do grupo de estacas | |
| Vd | – | força vertical máxima (incluindo o peso próprio do capeamento do grupo de estacas) | |
| Wp | – | peso próprio das estacas (apenas quando a opção “Considerar o peso próprio da estaca” estiver selecionado) |
Ao executar a análise de acordo com a teoria dos estados limite, o programa realiza a análise de verificação para um grupo de estacas em solo coesivo:
![]()
| onde: | Rg | – | capacidade de suporte vertical de um grupo de estacas |
| Vd | – | força vertical máxima (incluindo o peso próprio do capeamento do grupo de estacas) | |
| Wp | – | peso próprio das estacas (apenas quando a opção “Considerar o peso próprio da estaca” estiver selecionado) |
| γt | – | coeficiente de redução ca resistência global |
Ao realizar a análise de verificação de acordo com EN 1997-1, a capacidade de suporte vertical do grupo de estacas num solo coesivo é reduzida pelo coeficiente da resistência da base (γt = γb).
Assentamento de Um Grupo de Estacas
Solo não coesivo
A análise de um grupo de estacas num solo não coesivo é desenvolvida com base na teoria linear de assentamento (Poulos). A curva carga-assentamento para um grupo de estacas e o valor do assentamento total sg são aumentados pelo fator de assentamento do grupo gf.
O assentamento imediato do gripo de estacas, aumentado pelo fator de assentamento do grupo, é dado por:
![]()
![]()
| onde: | sg | – | assentamento do grupo de estacas |
| gf | – | fator de assentamento do grupo em solo não coesivo (segundo Pile Buck Inc. 1992) | |
| s0 | – | assentamento de uma estaca isolada (determinado, por ex., a partir da curva carga-assentamento) | |
| d | – | diâmetro da estaca | |
| bx | – | largura mínima do grupo de estacas |
Solo coesivo
O assentamento do grupo de estacas em solos coesivos é determinado como o assentamento de uma fundação fictícia, à profundidade 0,67*L, com largura B e comprimento B’.
A análises para calcular o assentamento são descritas com maior detalhe em “Análise de Assentamento”.
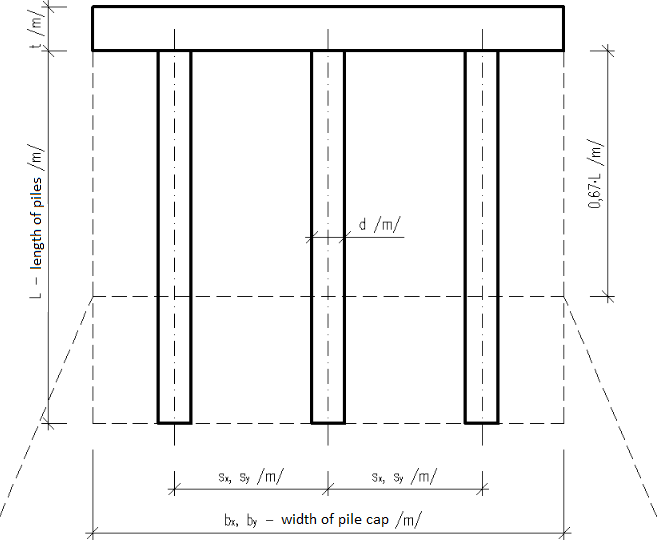 Esquema da fundação fictícia – assentamento do grupo de estacas em solo coesivo
Esquema da fundação fictícia – assentamento do grupo de estacas em solo coesivo
Método de Mola
O grupo de estacas é analisado através do Método dos Elementos Finitos. O capeamento do grupo de estacas é considerado como tendo rigidez infinita. Uma carga é aplicada no centro do capeamento e pode ser importada de um qualquer programa que execute a análise estática.
As estacas são analisadas de acordo com a figura:
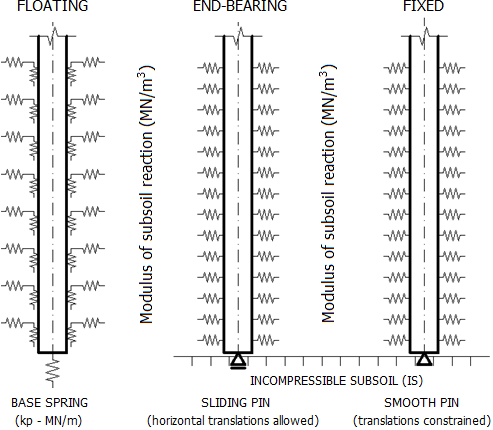 Modelação das estacas
Modelação das estacas
Estão disponíveis quatro opções para modelar as estacas, na janela “Configurações”:
- Estacas flutuantes – calcular a rigidez das molas a partir dos parâmetros do solo
- Estacas flutuantes – inserir rigidez das molas
- Estacas assentes em maciço rochoso
- Estacas fixadas em maciço rochoso
Todas as opções implicam a introdução do “módulo horizontal da reação do subsolo” que caracteriza o comportamento da estaca na direção transversal. As estacas flutuantes implicam, ainda, a determinação da rigidez das molas verticais. O programa permite o cálculo desta rigidez a partir dos parâmetros do solo disponíveis e da carga típica. Estes dados também podem ser inseridos automaticamente na janela “Molas verticais”.
A ligação entre as estacas e o capeamento do grupo de estacas pode ser considerada como uma rótula ou como um apoio fixo.
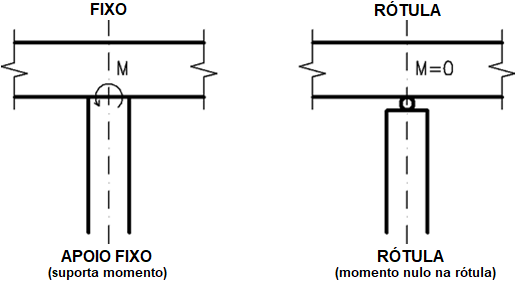 Ligação entre a estaca e o capeamento do grupo de estacas (selecionado na janela “Configurações”)
Ligação entre a estaca e o capeamento do grupo de estacas (selecionado na janela “Configurações”)
A própria análise da estrutura é executada através do método dos elementos finitos (MEF). Cada estaca é dividida em 10 elementos. Para cada elemento o programa define o valor das molas horizontais e verticais. Comparativamente a uma estaca isolada, a rigidez das molas horizontais e verticais é reduzida para as estacas interiores e exteriores – a rigidez horizontal é reduzida por coeficientes iguais a 0,5 e 0,25 para as estacas exteriores e interiores, respetivamente; a rigidez de cisalhamento é reduzida por coeficientes iguais a 0,5 e 0,1 para as estacas exteriores e interiores, respetivamente. Estas reduções representam o comportamento real da estrutura. As molas na base da estaca não são reduzidas.
Cálculo da Rigidez de Molas Verticais
Ao calcular a rigidez das molas verticais, é necessário introduzir a carga típica na janela “Molas verticais” que serve para determinar a rigidez da mola. Esta carga deve ser selecionada de forma a que caracterize o comportamento da estrutura da forma mais próxima da realidade possível.
A rigidez é determinada da seguinte forma:
- A carga típica é aplicada a cada estaca.
- A rigidez das molas verticais de cisalhamento distribuída ao longo das estacas é calculada com base nos parâmetros do solo.
- A rigidez da mola vertical na base da estaca é calculada com base na rigidez do subsolo abaixo da base da estaca e na profundidade da zona de influência. Para estacas à tração, esta rigidez é igual a zero.
Estas rigidez são depois ajustadas consoante a sua localização dentro do grupo de estacas – a rigidez de cisalhamento é reduzida por coeficientes iguais a 0.5 e 0.1 para estacas exteriores e interiores, respetivamente.
Microestaca
O programa realiza a análise de verificação de microestacas (reforçadas por um tubo metálico):
![]() com base nos estados limite
com base nos estados limite
![]() com base no fator de segurança
com base no fator de segurança
Tanto a secção da raiz como o tubo da microestaca (secção transversal da microestaca) podem ser examinadas por ambas as metodologias. Ao avaliar o tubo da microestaca, a análise pode incluir o tempo de vida útil expectável para a microestaca.
Verificação de acordo com o Fator de Segurança
O programa realiza a análise de verificação do tubo da microestaca e da raiz:
Verificação da secção transversal (tubo)
Tanto a estabilidade interna da secção como a capacidade de suporte da secção acoplada são verificadas.
1. Estabilidade interna da secção
![]()
| onde: | Ncr | – | força normal crítica normalizada, calculada consoante o método definido na secção “Microestacas” |
| Nmax | – | força normal máxima, inserida na janela “Carga” | |
| SFf | – | fator de segurança para a força crítica, inserido na secção “Microestacas” |
2. Capacidade de suporte da secção acoplada
![]()
| onde: | Rs | – | resistência do aço normalizada, inserida na janela “Material” |
| σs | – | tensão no aço, calculada de acordo com o método de carregamento (secção carregada apenas pela força normal ou pela combinação do momento fletor e da força normal) | |
| SFs | – | fator de segurança para a resistência da secção, inserido na secção “Microestacas” |
Verificação da raiz
![]()
| onde: | Q | – | capacidade de suporte da raiz normalizada, calculada consoante o método utilizado (ver “Capacidade de suporte da secção da raiz da microestaca”) |
| Nmax | – | força normal máxima, inserida na janela “Carga” | |
| SFr | – | fator de segurança para a resistência da raiz, inserido na secção “Microestacas” |
Verificação de acordo com os Estados Limite
O programa realiza a análise de verificação do tubo da microestaca e da raiz:
Verificação da secção transversal (tubo)
Tanto a estabilidade interna da secção como a capacidade de suporte da secção acoplada são verificadas.
1. Estabilidade interna da secção
![]()
| onde: | Nmax | – | força normal máxima, inserida na janela “Carga” |
| Ncrd | – | força normal crítica de dimensionamento |
![]()
| onde: | Ncr | – | força normal crítica normalizada, calculada consoante o método definido na secção “Microestacas” |
| γmf | – | coeficiente de redução da força crítica, inserido na secção “Microestacas” (estados limite) |
2. Capacidade de suporte da secção acoplada
![]()
| onde: | σs | – | tensão no aço, calculada de acordo com o método de carregamento (secção carregada apenas pela força normal ou pela combinação do momento fletor e da força normal) |
| Rsd | – | resistência do aço de dimensionamento |
![]()
| onde: | Rs | – | resistência do aço normalizada, inserida na janela “Material” |
| γss | – | coeficiente de confiabilidade do aço, inserido na secção “Microestacas” (estados limite) |
Verificação da raiz
![]()
| onde: | Nmax | – | força normal máxima, inserida na janela “Carga” |
| Qrd | – | capacidade de suporte da raiz normalizada |
![]()
| onde: | Q | – | capacidade de suporte da raiz normalizada, calculada consoante o método utilizado (ver “Capacidade de suporte da secção da raiz da microestaca”) |
| γr | – | coeficiente de redução da resistência da raiz, inserido na secção “Microestacas” (estados limite) |
Verificação do Tubo da Microestaca
Ao calcular a capacidade de suporte do tubo (secção transversal da microestaca), o programa diferencia o carregamento à tração ou à compressão da microestaca.
No caso do carregamento à tração, o programa determina a capacidade de suporte da secção acoplada (a resistência da mistura de cimento não é considerada).
No caso do carregamento à compressão, o programa avalia a capacidade de suporte da secção acoplada e a estabilidade interna da secção, dependendo do método definido na secção “Microestacas”.
Capacidade de Suporte da Secção Acoplada
No caso da capacidade de suporte da secção acoplada, o tubo da microestaca é verificado para a rotura devido à força normal ou à combinação do momento fletor e da força normal.
Ao determinar a capacidade de suporte da secção acoplada, é possível considerar a influência do tempo de vida útil da microestaca expectável.
Vida Útil da Microestaca
O tempo de vida útil da microestaca é considerado ao reduzir a área do tubo de reforço, através do coeficiente de redução da influência da corrosão do tubo metálico re e do coeficiente Fut que considera a conexão entre a microestaca e o solo envolvente.
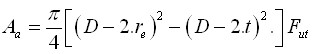
| onde: | D | – | diâmetro externo do tubo de reforço |
| t | – | espessura do tubo de reforço | |
| Fut | – | coeficiente que considera a conexão entre a microestaca e o solo envolvente (0,5 -1,0) | |
| re | – | coeficiente da influência da corrosão do tubo metálico |
Bibliografia:
BS EN 14199:2005 Execution of special geotechnical works. Micropiles British-Adopted European Standard / 30-Mar-2005 / 52 pages ISBN: 0580457249.
Coeficiente da Influência da Corrosão
Coeficiente da influência da corrosão do tubo metálico re [mm] (com base na EN 14199)
| Tipo de solo | Tempo de vida útil da microestaca [anos] | ||||
| 5 | 25 | 50 | 75 | 100 | |
| Solos em deposição natural | 0.00 | 0.30 | 0.60 | 0.90 | 1.20 |
| Solos em deposição natural contaminada | 0.15 | 0.75 | 1.50 | 2.25 | 3.00 |
| Solos orgânicos | 0.20 | 1.00 | 1.75 | 2.50 | 3.25 |
| Solos soltos | 0.18 | 0.70 | 1.20 | 1.70 | 2.20 |
| Solos especiais (contém sais solúveis) | 0.50 | 2.00 | 3.25 | 4.50 | 5.75 |
Note: os valores do coeficiente de influência da corrosão do tubo metálico re são para valores intermédios.
Capacidade de Suporte da Secção Transversal Carregada pela Força Normal
Força normal de tração
No caso de uma força de tração, a tensão na parte metálica da secção transversal é calculada através da seguinte fórmula:
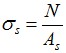
| onde: | σs | – | tenção no aço |
| N | – | força normal atuante na secção | |
| As | – | área da parte em aço da secção transversal da microestaca |
Força normal de compressão
A capacidade de suporte da secção transversal carregada à compressão é reduzida pelo coeficiente de curvatura, determinado por:
![]()
| onde: | χ | – | coeficiente de curvatura |
| As | – | área da parte em aço da secção transversal da microestaca | |
| Ac | – | área da parte da mistura de cimento da secção transversal da microestaca | |
| Rsd | – | resistência do aço de dimensionamento | |
| Rcd | – | resistência da mistura de cimento à compressão de dimensionamento |
As resistências de dimensionamento são iguais aos valores normalizados na verificação baseada no fator de segurança.
As resistências de dimensionamento do aço e da mistura de cimento, para a verificação baseada na teoria dos estados limite, da seguinte forma:
![]()
![]()
| onde: | Rs | – | resistência do aço normalizada, inserida na janela “Material” |
| γss | – | coeficiente de redução da resistência do aço, inserido na secção “Microestacas” | |
| Rc | – | resistência da mistura de cimento à compressão normalizada, inserida na janela “Material” | |
| γsc | – | coeficiente de redução da resistência da mistura de cimento, inserido na secção “Microestacas” |
A tensão na parte de aço da secção transversal é dada por:
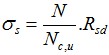
| onde: | N | – | força normal atuante na secção |
| Nc,u | – | capacidade de suporte da secção transversal carregada à compressão, reduzida pela influência da curvatura | |
| Rsd | – | resistência do aço de dimensionamento |
Capacidade de Suporte da Secção Transversal Carregada pela Combinação do Momento Fletor e da Força Normal
Uma secção transversal carregada pela combinação do momento fletor e da força normal, implica a determinação do eixo neutro, dividindo a secção transversal em numa parte tracionada e numa parte comprimida. Ao calcular a posição do eixo neutro, a influência da curvatura é incluída, isto é, a força normal é aumentada ao ser dividida pelo coeficiente de curvatura χ. O eixo neutro é obtido através do procedimento utilizado para o dimensionamento de secções transversais em concreto, reforçadas por aço, como um método de equilíbrio limite. A compressão é transmitida por uma parte do tubo de aço e do enchimento de mistura de cimento. A tensão é absorvida pela restante parte do tubo de aço, não sendo considerado que a mistura de cimento está tensionada.
A capacidade de suporte à flexão é determinada através da seguinte fórmula:
![]()
| onde: | Rsd | – | resistência do aço de dimensionamento |
| As,t | – | área da parte de aço tracionada da secção transversal da microestaca | |
| As,c | – | área da parte de aço comprimida da secção transversal da microestaca | |
| Ac,c | – | área da parte de mistura de cimento comprimida da secção transversal da microestaca | |
| ts,t | – | localização do centro da parte de aço tracionada | |
| ts,c | – | localização do centro da parte de aço comprimida | |
| tc,c | – | localização do centro da parte da mistura de cimento comprimida | |
| Rcd | – | resistência da mistura de cimento à compressão de dimensionamento |
As resistências de dimensionamento são iguais aos valores normalizados na verificação baseada no fator de segurança.
As resistências de dimensionamento do aço e da mistura de cimento, para a verificação baseada na teoria dos estados limite, da seguinte forma:
![]()
![]()
| onde: | Rs | – | resistência do aço normalizada, inserida na janela “Material” |
| γss | – | coeficiente de confiabilidade do aço, inserido na secção “Microestacas” | |
| Rc | – | resistência da mistura de cimento à compressão normalizada, inserida na janela “Material” | |
| γsc | – | coeficiente de confiabilidade da mistura de cimento, inserido na secção “Microestacas” |
A tensão na parte de aço da secção transversal é dada por:
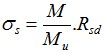
| onde: | M | – | momento fletor atuante na secção |
| Mu | – | capacidade de suporte à flexão | |
| Rsd | – | resistência do aço de dimensionamento |
Influência da Curvatura
A análise é precedida pela determinação das características de uma secção transversal ideal, em que o efeito da secção transversal da mistura de cimento é transformada em aço. A esbelteza do elemento é determinada através de:
![]()
| onde: | lcr | – | comprimento de curvatura do elemento |
| i | – | raio de giração da secção transversal ideal |
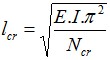
| onde: | E | – | módulo de elasticidade da secção transversal ideal |
| I | – | momento de inércia da secção transversal ideal | |
| Ncr | – | força normal crítica normalizada, calculada consoante o método selecionado na secção “Microestacas” |
A esbelteza recalculada λp é determinada por:
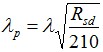
| onde: | Rsd | – | resistência do aço de dimensionamento (na análise baseada no fator de segurança, a resistência de dimensionamento é igual à resistência normalizada) |
![]()
| onde: | Rs | – | resistência do aço normalizada, inserida na janela “Material” |
| γss | – | coeficiente de confiabilidade do aço, inserido na secção “Microestacas” (estados limite) |
O coeficiente de curvatura χ é determinado de acordo com a esbelteza λp através das fórmulas seguintes:
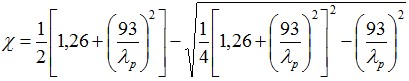 | |
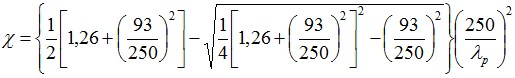 |
Estabilidade Interna da Secção
A estabilidade interna das secções serve para verificar a rotura da microestaca devido à curvatura no solo envolvente. O passo crucial para a determinação da estabilidade interna da secção é o cálculo da força normal Ncr, que depende do comprimento da microestaca, do solo envolvente e de outros efeitos. O usuário pode definir um dos seguintes métodos de análise, na secção “Microestaca”, para calcular a força normal crítica Ncr:
![]() Método geométrico (Euler)
Método geométrico (Euler)
![]() Teoria de Salas
Teoria de Salas
![]() Teoria de Véas-Souche
Teoria de Véas-Souche
Método Geométrico (Euler)
O solo que envolve a microestaca é representado, no programa, pelo módulo de reação do subsoloEp (constante de Winkler k), definido na janela “Cálculo da secção”. A figura mostra um modelo da estrutura.
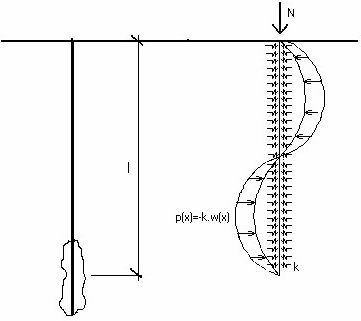 Modelo da estrutura
Modelo da estrutura
Para uma microestaca à compressão, é expectável que ocorra um número variável de meias ondas, dependendo da geometria e rigidez da estrutura e do solo envolvente. A solução para este caso é obtida através da equação da flexão de uma viga plana.
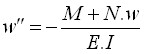
Após alguma manipulação, a equação para a flexão pode ser expressa como:
| onde: | |
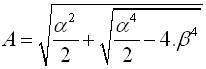 | |
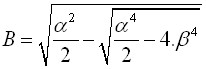 | |
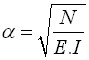 | |
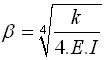 |
As constantes de integração C1–C4 são obtidas a partir das quatro condições de fronteira, consoante os apoios assumidos.
A força crítica Ncr é calculada através da fórmula (in [1]):
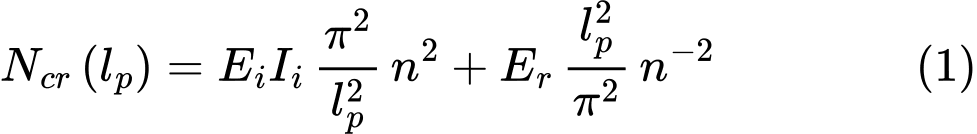
| onde: | Ei | – | módulo de Elasticidade da secção transversal ideal |
| Ii | – | momento de inércia da secção transversal ideal | |
| lp | – | comprimento efetivo da microestaca (comprimento livre + 1/2 comprimento da raiz) | |
| Er | – | reação do solo na direção horizontal | |
| n | – | número de meias ondas |
A força crítica Ncr é considerada como a função mínima (2). Esta é alcançada para o comprimento de meia onda:
![]()
O número de meias ondas n baseia-se na fórmula (3):
![]()
Caso uma parte da microestaca esteja acima da superfície do terreno (deslocamento da cabeça da estaca), os valores reduzidos de n e Er são calculados de acordo com:
![]()
![]()
| onde: | lv | – | comprimento da microestaca acima da superfície do terreno |
Assumindo a condição rótula-rótula, deve-se utilizar a equação seguinte:
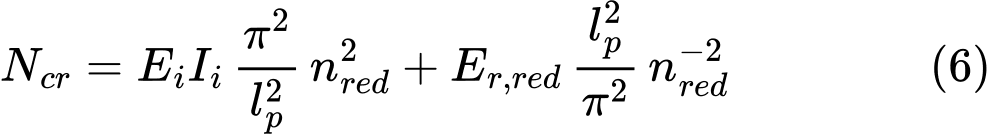
Assumindo a condição rótula-apoio fixo, deve-se utilizar a equação seguinte:
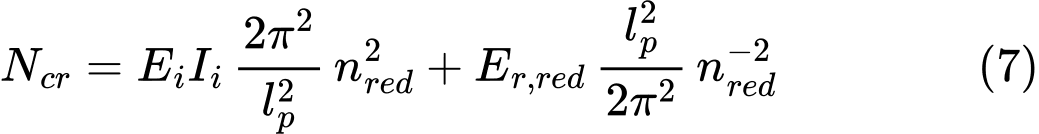
Bibliografia:
[1] Timoshenko, S. P.: Theory of Elastic Stability, New York, 1936
Teoria de Salas
A força crítica Ncr para as condições básicas de apoio na cabeça da microestaca (que determinam a deflexão da microestaca), é dada por:
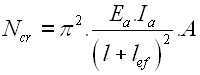
| onde: | Ea*Ia | – | rigidez de flexão do tubo de reforço da microestaca |
| l | – | comprimento livre da microestaca | |
| lef | – | comprimento da extremidade fixa fictícia | |
| A | – | constante que reflete o tipo de apoio na cabeça da microestaca |
![]()
| onde: | f | – | coeficiente que depende do rácio entre os módulos de elasticidade do solo na cabeça e na base da microestaca |
| le | – | comprimento elástico da microestada, dado por: |
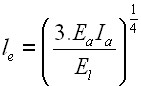
| onde: | Ea*Ia | – | rigidez de flexão do tubo de reforço da microestaca |
| El | – | módulo de elasticidade do solo na base da microestaca |
Bibliografia:
Jiménez Salas J.A. a kol:Geotecnica y Cimientos III, Capitulo 3, Rueda, Madrid (Spanish).
Constante A que Reflete o Tipo de Apoio da Cabeça da Microestaca
Constante A que reflete o tipo de apoio na cabeça da microestaca
| Tipo de apoio na cabeça da microestaca | A [-] |
| Rótula | 2.045 |
| Livre | 0.25 |
| Fixo | 4.0 |
| Móvel na direção horizontal | 1.0 |
Coeficiente f
Coeficiente f
| Eo / El 1) [-] | f [-] |
| 0 | 1.70 |
| 0.5 | 1.25 |
| 1 | 1.00 |
1) Eo – módulo de elasticidade do solo abaixo da superfície do terreno (na cabeça da microestaca)
El – módulo de elasticidade do solo na raiz da microestaca
Teoria de Véas-Souche
A força crítica Ncr é calculada de acordo com a fórmula [1]:
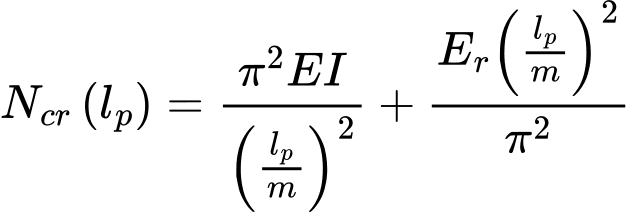
| onde: | lp | – | comprimento efetivo da microestaca (comprimento livre + 1/2 comprimento da raiz) |
| EI | – | rigidez à flexão do tubo de reforço da microestaca | |
| Er | – | reação do solo na direção horizontal | |
| m | – | número de meias ondas |
A força crítica Ncr é considerada como a função mínima (2). Esta é alcançada para o comprimento de meia onda:
![]()
O número de meias ondas n baseia-se na fórmula (3):
![]()
O parâmetro adimensional ω é calculado de acordo com a fórmula (4):
![]()
| onde: | lv | – | comprimento da microestaca acima da superfície do terreno |
O outro quantificador adimensional é obtido através da fórmula (5):
![]()
A relação entre as fórmulas (3), (4) e (5) está descrita no artigo [2] através de gráficos. A força crítica Ncr é calculada a partir do quantificador adimensional (5), que é determinado a partir de gráficos para os valores conhecidos de ω e m.
Bibliografia:
[1] Timoshenko, S. P.: Theory of Elastic Stability, New York, 1936[2] Véase, Souche: Étude du fla,berment de pieux partiellernent immergés dans offrant latéralement une réaction élastique pure, Annales de I’ITBTP, No. 423, Sene Soils et Foundations, 187, mars – avril 1984, str. 38 – 60 (in French)
Módulo da Reação Horizontal do Subsolo
O solo que envolve a microestaca pode ser representado através de molas horizontais ao longo da microestaca, caracterizadas pela constante de Winkler kh. Para a curvatura da microestaca no solo, na direção do eixo x, pode ser considerada a seguinte equação:
![]()
| onde: | ph | – | reação do solo causada pelo deslocamento da microestaca na direção do eixo x (solo à compressão) |
| kh | – | rigidez da mola de Winkler (módulo de reação do subsoloEp) | |
| x | – | deslocamento da microestaca na direção do eixo x |
Se se considerar que a reação do solo para pressionar a microestaca por metro de desenvolvimento da microestaca, esta á dada por:
![]()
| onde: | Er | – | reação do solo na direção horizontal |
| ph | – | reação do subsolo devido ao deslocamento da microestaca na direção do eixo x por metro de desenvolvimento | |
| x | deslocamento da microestaca na direção do eixo x |
As equações apresentadas acima identificam a relação entre o módulo de reação do subsoloEp [kN/m3] e a reação do solo na direção horizontal Er [kN/m2] (assumindo que Er é constante no solo):
![]()
| onde: | D | – | diâmetro da microestaca |
| kh | – | rigidez da mola de Winkler (módulo de reação do subsoloEp) |
A reação do solo na direção horizontal Er pode ser calculada com base no módulo pressiométrico Em.
Calculo do Módulo de Reação Horizontal do Subsolo Er
O módulo de reação horizontal do subsolo pode ser determinado a partir do módulo pressiométricoEm e do coeficiente αp:
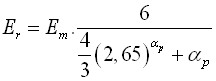
| onde: | Em | – | módulo pressiométrico (Menard) [MPa] |
| αp | – | fator reológico do solo (ver tabela abaixo) |
Valores de referência para Em e Plim
| Solos | Em[Mpa] | Plim [MPa] | |
| não coesivos | solo | 0 – 3.5 | 0 – 0.5 |
| mediamente denso | 3.5 – 12 | 0.5 – 1.5 | |
| denso | 12 – 22.5 | 0.5 – 2.5 | |
| muito denso | > 22.5 | > 2.5 | |
| coesivos | lama | 0 – 2.5 | 0 – 0.2 |
| mole | 2.5 – 5 | 0.2 – 0.4 | |
| rígido | 5 – 12 | 0.4 – 0.8 | |
| sólido | 12 – 25 | 0.8 – 1.6 | |
| duro | > 25 | > 16 |
Valores para o fator reológico αp para várias condições do solo
| Tipo de solo | Turfa | Argila, silte | Sedimentar | Areia | Areia e cascalho | ||||
| αp | Em / Plim | αp | Em / Plim | αp | Em / Plim | αp | Em / Plim | αp | |
| pré-consolidado | 1 | > 16 | 1.0 | > 14 | 0.67 | > 12 | 0.5 | > 10 | 0.33 |
| normalmente consolidado | 1 | 9 – 16 | 0.67 | 8 – 14 | 0.5 | 7 – 12 | 0.33 | 6 – 10 | 0.25 |
| sobreconsolidado | – | 7 – 9 | 0.5 | 5 – 8 | 0.5 | 5 – 7 | 0.5 | – | 0.25 |
Bibliografia:
Menard, L. F.: Proceedings of the 6th International Conference on Soil Mechanics and Foundation Engineering, Montreal, Vol. 2, 1965, pp. 295 – 299 (table 2.29 a 2.30).
Valores para o Módulo de Reação do Subsolo Ep
Valores para o módulo de reação do subsolo Ep = kh [MN/m3]
| Solo | Ep Min/Max [MN/m3] | Valor médio kh = Ep [MN/m3] |
| argila mole | 2 – 5 | 3.5 |
| argila rígida | 3 – 8 | 5.5 |
| argila sólida | 6 – 16 | 11 |
| areia naturalmente molhada solta | 6 – 13 | 9.5 |
| areia naturalmente molhada mediamente densa | 20 – 40 | 30 |
| areia naturalmente molhada densa | 45 – 90 | 67.5 |
| areia aquífera solta | 4 – 8 | 6 |
| areia aquífera mediamente densa | 10 – 20 | 15 |
| areia aquífera densa | 30 – 60 | 45 |
| argila arenosa mole | 3 – 6 | 4.5 |
| argila arenosa rígida | 5 – 9 | 7 |
| argila arenosa sólida | 8 – 17 | 12.5 |
| areia argilosa molhada solta | 4 – 9 | 6.5 |
| areia argilosa molhada mediamente densa | 12 – 32 | 22 |
| areia argilosa molhada densa | 24 – 44 | 34 |
| areia argilosa aquífera solta | 3.5 – 6.5 | 5 |
| areia argilosa aquífera mediamente densa | 7 – 11 | 9 |
| areia argilosa aquífera densa | 11.5 – 13.5 | 12.5 |
Capacidade de Suporte da Secção da Raiz da Microestaca
A capacidade de suporte da microestaca pode ser determinada computacionalmente, através de uma das metodologias disponíveis na bibliografia a Normas. O programa “Microestaca” contém um conjunto de métodos que representam as metodologias básicas para a análise da capacidade de suporte da raiz da microestaca. A análise é realizada de acordo com o definido na secção “Microestacas”, de modo a aplicar um dos seguintes procedimentos:
| teoria de Lizzi | – | o atrito limite médio da superfície da raiz é especificado |
| teoria de Littlejohn | – | a pressão da argamassa é especificada |
| teoria de Zweck | – | o método depende da tensão geostática e dos parâmetros do solo envolvente |
| teoria de Bowles | o método depende da tensão geostática e dos parâmetros do solo envolvente | |
| teoria de Véas | – | o método de execução da microestaca e os parâmetros do solo envolvente são especificados |
| raiz em rocha | – | os parâmetros da rocha do solo envolvente são especificados |
| Bustamante | – | o método depende dos parâmetros de ensaios SPT ou de ensaios pressiométricos (PMT) |
Teoria de Lizzi
O método de Lizzi é o método mais utilizado. A capacidade de suporte da raiz é dada por:
![]()
| onde: | d | – | diâmetro da raiz |
| l | – | comprimento da raiz | |
| τm | – | atrito superficial médio limite | |
| J | – | coeficiente que reflete a influência do furo |
O coeficiente J reflete a influência do diâmetro do furo – pode variar entre 1.0, para diâmetros até 100 mm, e 0.8, para diâmetros até 200 mm.
O atrito superficial médio limite da raiz da microestaca pode ser encontrado na bibliografia. O programa contém três tabelas com valores de referência para o atrito superficial limite. A primeira foi criada pelos autores do programa, com base em diferentes fontes bibliográficas. A segunda, contém os valores para τm propostos em DIN 4128. A terceira, contém os valores propostos por Klein e Mišov (Inženýrské stavby, 1984). A terceira tabela contém valores para o atrito superficial limite da raiz de microestacas em vários solos, diâmetros da raiz, número de camadas de argamassa, etc. – através dos valores desta tabela é possível obter resultados realistas.
Bibliografia:
Lizzi, F. (1982). “The pali radice (root piles)”. Symposium on soil and rockimprovement techniques including geotextiles, reinforced earth and modern pilingmethods, Bangkok, D-3.
Atrito Superficial da Raiz da Microestaca
Valores de referência para o atrito superficial limite (recomendado pelos autores)
| Solo | Atrito superficial [kPa] |
| argila mole | 40 – 60 |
| argila rígida | 65 – 85 |
| argila sólida | 130 – 170 |
| areia naturalmente molhada, solta | 110 – 150 |
| areia naturalmente molhada, mediamente densa | 140 – 180 |
| areia naturalmente molhada, densa | 170 – 230 |
| areia aquífera, solta | 80 – 130 |
| areia aquífera, mediamente densa | 120 – 160 |
| areia aquífera, densa | 160 – 200 |
| argila arenosa, mole | 50 – 70 |
| argila arenosa, rígida | 75 – 95 |
| argila arenosa, sólida | 125 – 165 |
| areia argilosa, molhada, solta | 90 – 135 |
| areia argilosa, molhada, mediamente densa | 135 – 165 |
| areia argilosa, molhada, densa | 150 – 170 |
| areia argilosa, aquífera, solta | 80 – 105 |
| areia argilosa, aquífera, mediamente densa | 90 – 130 |
| areia argilosa, aquífera, densa | 115 – 155 |
Valores de referência para o atrito superficial limite de acordo com DIN 4128
| Solo | Atrito superficial médio limite | |
| estacas à compressão [kPa] | estacas à tração [kPa] | |
| areia de graduação média a grosseira | 200 | 100 |
| areia e cascalho | 150 | 80 |
| solos coesivos | 100 | 50 |
Parâmetros recomendados para a raiz das ancoragens (Mišove, Klein, Inženýrské stavby 5/1986)
| Tipo de apoio na cabeça da microestaca | Pressão na camada de argamassa final [MPa] | Número de camadas de argamassa | Diâmetro da raiz [mm] | Comprimento da raiz [m] | Atrito superficial [kPa] |
| bedrock | – | 0 | 120 | 5 – 3 | 1000 – 1600 |
| semirock | 0.5 – 3.0 | 0 – 1 | 120 – 220 | 7 – 3 | 300 – 1000 |
| cascalho, solos injetáveis | 1,0 | 1 – 2 | 250 – 400 | 7 – 5 | 250 – 320 |
| cascalho, solos não injetáveis | 2.0 – 4.0 | 1 – 2 | 280 – 350 | 7 – 5 | 230 |
| areia de graduação média e fina | 1.5 – 4.0 | 2 – 3 | 220 – 350 | 12 – 7 | 150 – 180 |
| solos com coesão rígida e sólidos | 1.5 – 3.0 | 1 – 3 | 200 – 280 | 17 – 8 | 130 – 190 |
| solos coesivos sólidos a plásticos rígidos | 1.0 – 2.5 | 2 – 3 | 150 – 400 | 20 – 9 | 100 – 130 |
| solos coesivos plásticos moles | 0.5 – 2.0 | 3 – 4 | 300 – 450 | 27 – 13.5 | 50 – 70 |
Teoria de Littlejohn
Ao utilizar o método de Littlejohn, a capacidade de suporte da raiz é dada por:
![]()
| onde: | d | – | diâmetro da raiz |
| l | – | comprimento da raiz | |
| pi | – | valor da pressão na argamassa |
A partir de ensaios experimentais em microestacas, verificou-se que a sua capacidade de carga também depende da progressão e pressão da argamassa (normalmente, a progressão da argamassa define a capacidade de suporte da microestaca). A capacidade de suporte aumenta consideravelmente com injeções de argamassa repetidas. A pressão na argamassa pode variar entre 0.1 e 3 Mpa, sendo que alguns casos pode chegar a 8 Mpa. O método de Littlejohn permite obter a capacidade de suporte diretamente proporcional à pressão na argamassa.
Bibliografia:
LITTLEJOHN, G. S. y BRUCE, D. A. (1975).: “Rock Anchors – State of the Art. Part 1. Design”. En Ground Engineering, Vol. 8, N° 4.
Teoria de Zweck
O método de Zweck e Bowles foi desenvolvido para análise da raiz de ancoragens – depende principalmente da tensão geostática na zona da raiz da microestaca. Este método parte dos mesmo princípios – o valor da pressão é, no entanto, reduzida através do coeficiente da pressão em repouso Ko.
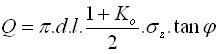
![]()
| onde: | d | – | diâmetro da raiz |
| l | – | comprimento da raiz | |
| Ko | – | valor da pressão em repouso | |
| σz | – | tensão geostática média na raiz da microestaca | |
| φ | – | valor do ângulo de atrito médio na raiz da microestaca |
Teoria de Bowles
O método de Bowles permite considerar a influência da coesão da capacidade de suporte da raiz – é mais apropriada para solos coesivos.
![]()
![]()
| onde: | d | – | diâmetro da raiz |
| l | – | comprimento da raiz | |
| Ko | – | coeficiente da pressão em repouso | |
| σz | – | tensão geostática média na raiz da microestaca | |
| φ | – | valor do ângulo de atrito interno médio na raiz da microestaca |
Bibliografia:
J.E. Bowles – Foundation Analysis and Design, McGraw Hill book Company.
Teoria de Véas
Esta análise considera o efeito da tensão geostática na raiz da microestaca e o percurso da argamassa.
A capacidade de suporte da raiz da microestaca é dada por:
![]()
| onde: | Rbk | – | capacidade de suporte da raiz da microestaca |
| Rsk | – | capacidade de suporte da superfície da microestaca |
Capacidade de suporte da superfície da microestaca:
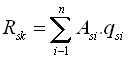
| onde: | n | – | número de camadas atravessadas pela microestaca |
| Asi | – | área da base da microestaca na iésima camada | |
| qsi | – | atrito superficial na iésima camada |
A capacidade de suporte da raiz da microestaca é dada por:
![]()
O atrito superficial qs à profundidade z, medida a partir da da superfície do terreno, é dado por:
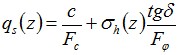
| onde: | z | – | profundidade z abaixo da superfície do terreno, onde o valor do atrito superficial é determinado |
| c | – | coesão efetiva do solo à profundidade z | |
| δ | – | ângulo de atrito ao longo da interface da raiz microestaca e o solo à profundidade z: | |
| φ’ | – | ângulo de atrito interno efetivo do solo à profundidade z | |
| σh(z) | – | componente horizontal da tensão geostática à profundidade z: | |
| – | para argamassas com percurso IR e IRS (com monitorização da pressão na argamassa) e profundidade z ≥ 5 m: | ||
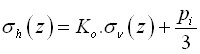 | |||
| – | outros casos: | ||
| Ko | – | coeficiente do empuxo de terra em repouso | |
| – | para solos normalmente consolidados: | ||
| – | para solos sobreconsolidados: | ||
| σv(z) | – | componente vertical da tensão geostática à profundidade z | |
| pi | – | pressão na argamassa para percurso do tipo IR e IRS, e profundidade z ≥ 5 m, em outros casos pi = 0 | |
| Fc, Fφ | – | coeficientes para o tipo de aplicação da microestaca |
Bibliografia:
Véas, Souche : Étude du flambement de pieux partiellement immergés dans un milieu offrant latéralement une réaction élastique pure, Annales de l’ITBTP, No. 423, Sene Soils et Foundations, 187, mars – avril 1984, p. 38 – 60 (French).
Coeficientes para o Tipo de Aplicação da Microestaca
Coeficientes para o tipo de aplicação da microestaca
| Tipo de aplicação da microestaca | Fc [-] | Fφ [-] |
| Fundações construídas recentemente | 1.50 | 1.50 |
| Fundações existentes | 1.20 | 1.20 |
Capacidade de Suporte da Raiz em Rocha
Esta solução é apropriada quando a raiz da microestaca atinge rochas de índice RQD > 60, ou com resistência à compressão simples σc > 20 MPa (ISRM < III). A capacidade de suporte da raiz é dada por:
![]()
| onde: | As | – | área da parede da raiz da microestaca |
| qsr | – | atrito superficial da rocha | |
| Ab | – | área da raiz da microestaca | |
| qbr | – | capacidade de suporte da raiz da microestaca na rocha |
Bibliografia:
Guía para el proyecto y la ejecución de micropilotes en obras de carretera, Ministerio de fomento, 2005 (Spanish).
Atrito Superficial e Capacidade de Suporte da Raiz da Microestaca em Rocha
Atrito superficial na rocha qsr e capacidade de suporte da raiz da microestaca na rocha qbr
| Tipo de rocha | qsr [MPa] | qbr [MPa]1)1 |
| Sedimentos | 0.15 – 0.40 | 0.07σc |
| Ardósias e filitos | 0.20 – 0.30 | 0.07σc |
| Arenitos | 0.30 – 0.45 | 0.07σc |
| Calcários e dolomites | 0.40 – 0.50 | 0.10σc |
| Granitos e basaltos | 0.40 – 0.60 | 0.10σc |
1) σc – resistência à tensão simples MPa
Bustamante (SPT, Pressiómetro PMT)
A análise da capacidade de suporte da secção da raiz da microestaca baseia-se nos resultados dos ensaios de penetração (SPT) ou ensaios pressiométricos (PMT).
O valor do atrito superficial da raiz da microestaca qs [MPa] pode ser obtido a partir dos gráficos de Bustamante, que dependem do tipo de solo e da tecnologia de injeção.
A resistência do furo na raiz da microestaca Rs é dada por:
![]()
| onde: | dr | – | diâmetro da raiz da microestaca |
| lr | – | comprimento da raiz da microestaca | |
| qs | – | atrito superficial da raiz da microestaca (valor determinado a partir do gráfico) |
A resistência da base da raiz da microestaca Rb pode não ser considerada na análise, ou ser calculada como:
![]()
| onde: | Rs | – | resistência do furo na raiz da microestaca |
No programa, é assumido que a resistência da base na raiz da microestaca Rb é calculada através de:
![]()
| onde: | Ap | – | área da secção transversal da base da raiz da microestaca |
| kp | – | fator do solo na vizinhança da base da raiz da microestaca | |
| pLM | – | pressão limite segundo Menard |
Atrito Superficial da Raiz da Microestaca – Gráficos
A análise da resistência do furo na raiz da microestaca Rs depende consideravelmente do tipo de injeção da raiz da microestaca. As seguintes opções de injeção são consideradas no programa:
![]() IRS: injeção seletiva repetida na raiz da microestaca por mangas, executada no local (Tube-á-Manchette),
IRS: injeção seletiva repetida na raiz da microestaca por mangas, executada no local (Tube-á-Manchette),
![]() IGU: injeção sob pressão global unificada (Looped Tube Systems).
IGU: injeção sob pressão global unificada (Looped Tube Systems).
Os gráficos seguintes, utilizados para a análise do atrito superficial da raiz da microestaca qs [MPa], são considerados pelo programa:
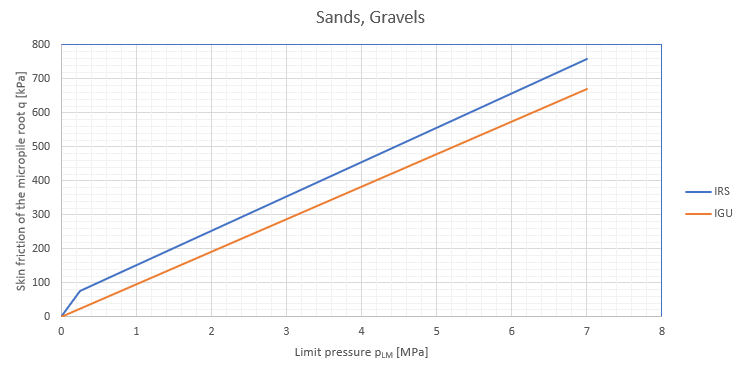
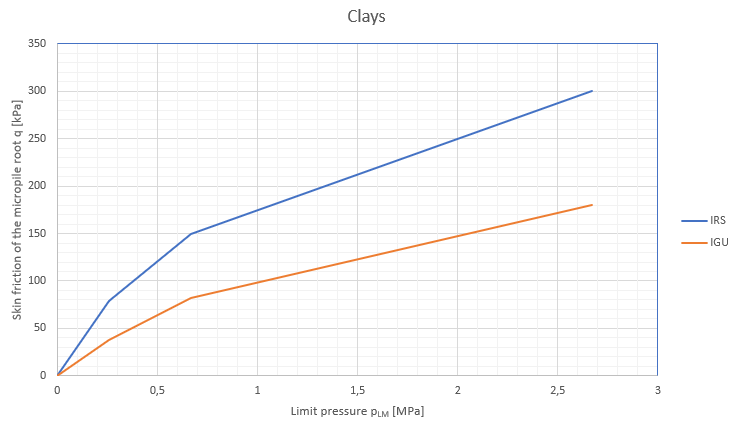
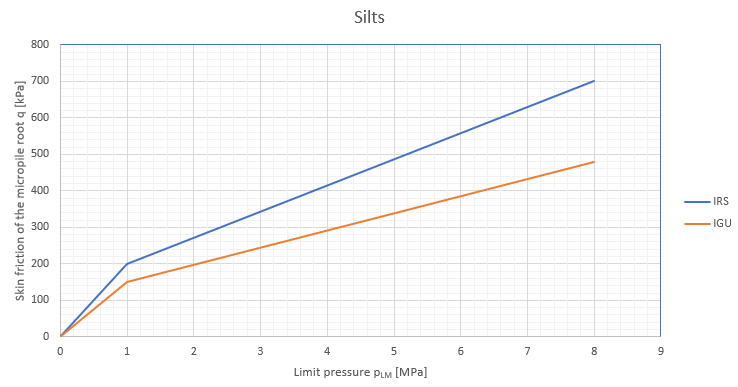
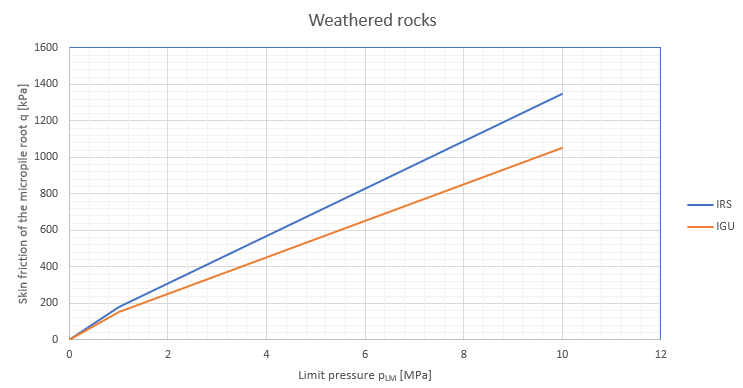
Os gráficos exibidos mostram a pressão limite pLM no eixo horizontal, determinada a partir de ensaios pressiométricos (PMT). Para as sondagens SPT são utilizados os mesmo gráficos, mas a pressão limite pLM [MPa] é determinada como n-vezes o número de pancadas N para o intervalo da profundidade de penetração d = 0.3 m, isto é, SPT [N/0.3 m]. Para cada tipo de solo, os valores da pressão limite pLM segundo Menard são os seguintes:
![]() areia, cascalho, silte e rocha fraca: pLM = SPT / 20,
areia, cascalho, silte e rocha fraca: pLM = SPT / 20,
![]() argilas: pLM = SPT / 15.
argilas: pLM = SPT / 15.
Por exemplo, para solos arenosos e com o valor para o número de pancadas SPT = 120, a pressão limite é dada por pLM = SPT / 20 = 120 / 20 = 6.0 MPa.
Para solos argilosos e com valor para o número de pancadas SPT = 30, a pressão limite é dada por pLM = SPT / 15 = 30/15 = 2.0 MPa.
O eixo vertical apresenta o valor do atrito superficial da raiz da microestaca qs, em função da pressão limite pLM e do tipo de injeção aplicada (IRS ou IGU).
Ensaios de Campo
O programa “Estratigrafia” e alguns outros programas GEO5, permitem a introdução de dados utilizados como parâmetros de análise obtidos a partes destes ensaios de campo:
![]() CPT – Ensaio de penetração de cone – programas “Estaca via CPT” e “Sapata via CPT”
CPT – Ensaio de penetração de cone – programas “Estaca via CPT” e “Sapata via CPT”
![]() DPT – Ensaio de carregamento dinâmico
DPT – Ensaio de carregamento dinâmico
![]() SPT – Ensaio de sondagem à percussão – programas “Microestaca”, “Estaca via CPT” e “Sapata via CPT”
SPT – Ensaio de sondagem à percussão – programas “Microestaca”, “Estaca via CPT” e “Sapata via CPT”
![]() PMT – Ensaio pressiométrico – programas “Verificação de Contenções”, “Estaca Anti-Deslizante”, “Microestaca” e “Sapata via ECPT”
PMT – Ensaio pressiométrico – programas “Verificação de Contenções”, “Estaca Anti-Deslizante”, “Microestaca” e “Sapata via ECPT”
![]() DMT – Ensaio dilatométrico – programas “Sapata”, “Verificação de Contenções” e “Estaca Anti-Deslizante”
DMT – Ensaio dilatométrico – programas “Sapata”, “Verificação de Contenções” e “Estaca Anti-Deslizante”
Ensaio de Penetração de Cone (CPT)
O ensaio de penetração de cone (CPT) consiste em empurrar um cone de penetração com recurso a um sistema de varas de penetração com velocidade constante de 20 – 25 mm/s no solo. Durante o ensaio de penetração, são registados os valores da resistência de coneqc e do atrito superficial localfs. A resistência de cone representa a resistência contra a penetração de um espigão cónico no solo (subsolo). O diâmetro da ponta do cone tem, normalmente, 25 – 50 mm.
A resistência de cone qc [MPa] representa o rácio da força registada na ponta do cone Qc e a área da projeção normal da ponta do cone Ac.
O atrito superficial local fs [kPa] representa o rácio da força registada na manga de atrito Fs e a área da sua superfície As.
O resultado do ensaio de penetração de cone é uma distribuição em forma de gráfico.
O ensaio de penetração de cone (CPT) serve de parâmetro a introduzir para as análises nos programas “Estaca via CPT” e “Sapata via CPT” e para a modelação estratigráfica no programa “Estratigrafia”.
Os ensaios CPT podem ser importados para o programa através do botão “Importar“. O procedimento de tabelas de dados (*.txt) é descrito com mais detalhe aqui.
O nome do ensaio CPT e o deslocamento vertical em relação à origem devem ser introduzidos na caixa de diálogo “Novo ensaio de campo“. No programa “Estratigrafia“, é necessário introduzir as coordenadas x, y, z.
Os valores medidos da resistência de cone qc são introduzidos na tabela.
Ao calcular a capacidade de suporte da estaca, de acordo com a teoria de Schmertmann, o atrito local fs deve ser introduzido.
Ao realizar a classificação dos solos, os valores da pressão nos poros u2 devem ser introduzidos. Se a pressão nos poros não foi obtida (CPTu), esta pode ser calculada a partir do nível freático definido, através do botão “Calcular u2″.
Caixa de diálogo “Novo ensaio de campo”
Bibliografia:
EN ISO 22476-1: Geotechnical investigation and testing – Field testing. Part 1: Electrical cone and piezocone penetration test, 2013.
EN ISO 22476-12: Geotechnical investigation and testing – Field testing. Part 12: Mechanical cone penetration test (CPTM), 2009.
Roy E. Hunt: Geotechnical Engineering Investigation Handbook, Second Edition (CRC Press, 2005)
Classificação dos Solos Segundo Robertson
Na classificação dos solos segundo Robertson (1986 ou 2010) não é necessário inserir parâmetros dos solos, uma vez que o programa executa este passo automaticamente, com a sua atribuição ao perfil geológico. Por esta razão, a avaliação do CPT realizado é muito rápida e especialmente clara.
A classificação dos solos segundo Robertson (1986 ou 2010) baseia-se nos valores obtidos para a resistência à penetração qc [MPa], atrito superficial local fs [kPa] e pressão nos poros u2 [kPa]. Com base no valor corrigido da resistência de cone qt = qc + u2 * (1 – a), ou do rácio de percentagem qc /pa e rácio de atrito Rf = fs /qt, o programa executa automaticamente a atribuição do tipo de comportamento do solo (SBT) de acordo com o gráfico seguinte. pa – pressão atmosférica = 100 kPa (= 1 tsf).
 Gráfico do Tipo de Comportamento do Solo (SBT) para CPT não normalizados segundo Robertson, 1986 (fonte: Robertson et al., 1986)
Gráfico do Tipo de Comportamento do Solo (SBT) para CPT não normalizados segundo Robertson, 1986 (fonte: Robertson et al., 1986)
Classificação dos solos segundo Robertson, 1986 (fonte: Robertson et al., 1986)
| Zona | Tipo de Comportamento do Solo (SBT) |
| 1 | Graduação fina sensível |
| 2 | Material Orgânico |
| 3 | Argila |
| 4 | Argila siltosa a argila |
| 5 | Silte argiloso a argila siltosa |
| 6 | Silte arenoso a silte argiloso |
| 7 | Areia siltosa a silte arenoso |
| 8 | Areia a areia siltosa |
| 9 | Areia |
| 10 | Areia grossa a areia |
| 11 | Muito rígido com graduação fina * |
| 12 | Areia a areia argilosa * |
* Solo sobreconsolidado ou cimentado
 Gráfico do Tipo de Comportamento do Solo (SBT) para CPT não normalizados segundo Robertson, 2010 (fonte: [6], Figure 21, pp. 26)
Gráfico do Tipo de Comportamento do Solo (SBT) para CPT não normalizados segundo Robertson, 2010 (fonte: [6], Figure 21, pp. 26)
Classificação dos solos segundo Robertson, 2010 (fonte: [6], Figure 21, pp. 26)
| Zona | Tipo de Comportamento do Solo (SBT) |
| 1 | Sensível, graduação fina |
| 2 | Solos orgânicos – argila |
| 3 | Argila – argila siltosa a argila |
| 4 | Misturas de silte – silte argiloso a argila siltosa |
| 5 | Misturas de areia – areia siltosa a silte arenoso |
| 6 | Areias – areia limpa a areia siltosa |
| 7 | Areia grossa a areia densa |
| 8 | Areia muito rígida a areia argilosa * |
| 9 | Muito rígido com graduação fina * |
* Extremamente sobreconsolidade ou cimentado
A nova classificação de solos segundo Robertson (2010) contém um número menor de classes de solos em relação à classificação de solos original de 1986. No entanto, a classificação de solos de acordo com Robertson (2010) é mais exata e mais utilizada.
Se a opção “calcular” for selecionada para o peso volúmico do solo, na janela “Classificação do solo“, o peso volúmico do solo γ [kN/m3] é determinado através da fórmula seguinte:
| onde: | γw | – | peso volúmico da água (≈10) [kN/m3] |
| pa | – | pressão atmosférica (≈100) [kPa] |
![]()
| onde: | Rf | – | rácio de atrito entre o atrito superficial e resistência de cone |
 Peso volúmico adimensional do solo γ/γw baseado em CPTs (fonte: [6], Figure 28, pp. 36)
Peso volúmico adimensional do solo γ/γw baseado em CPTs (fonte: [6], Figure 28, pp. 36)
A introdução da espessura das camadas do solo influencia a espessura mínima da camada do iésimo solo. No caso de zero camadas de solo, estão atribuídas todas as camadas de solo com base na classificação segundo Robertson (1986 ou 2010), no perfil geológico.
Ao introduzir uma espessura mínima da camada diferente de zero, o número de camadas do solo é reduzido no perfil geológico. O perfil e o número de camadas de solo afetam a capacidade de suporte vertical e o assentamento de estacas ou de sapatas de fundação, analisados por CPT.
Bibliografia:
[1] EN ISO 22476-1: Geotechnical investigation and testing – Field testing. Part 1: Electrical cone and piezocone penetration test, 2013.
[2] EN ISO 22476-12: Geotechnical investigation and testing – Field testing. Part 12: Mechanical cone penetration test (CPTM), 2009.
[3] Robertson, P. K.: Interpretation of Cone Penetration Tests – a unified approach. Canadian Geotechnical Journal, 2009, No. 46, pp. 1337 – 1355.
[4] Robertson, P. K. and Cabal, K. L.: Guide to Cone Penetration Testing for Geotechnical Engineering. Gregg Drilling & Testing, Inc., USA, 6th edition, 2014, 133 p.
Coeficiente do Penetrómetro (Rácio de Área Útil)
Este coeficiente α [–] representa a rácio de área útil que é determinado a partir de uma medição calibrada em laboratório (o esforço para eliminar os efeitos adversos da manga de atrito e da ponta do cone desigual). Os valores típicos para este coeficiente estão compreendidos dentro do intervalo 0.7 a 0.85.
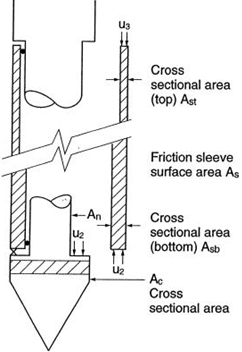 Efeitos da área desigual na ponta do cone e manga de atrito (fonte: [6], Figure 20, pp. 22)
Efeitos da área desigual na ponta do cone e manga de atrito (fonte: [6], Figure 20, pp. 22)
Bibliografia:
[1] EN ISO 22476-1: Geotechnical investigation and testing – Field testing. Part 1: Electrical cone and piezocone penetration test, 2013.
[2] EN ISO 22476-12: Geotechnical investigation and testing – Field testing. Part 12: Mechanical cone penetration test (CPTM), 2009.
[3] Robertson, P. K.: Interpretation of Cone Penetration Tests – a unified approach. Canadian Geotechnical Journal, 2009, No. 46, pp. 1337 – 1355.
[4] Robertson, P. K. and Cabal, K. L.: Guide to Cone Penetration Testing for Geotechnical Engineering. Gregg Drilling & Testing, Inc., USA, 6th edition, 2014, 133 p.
Importar CPT
Os programas “Estaca via CPT“, “Sapata via CPT” e “Estratigrafia” permitem importar resultados de ensaios CPT em vários formatos.
A caixa de diálogo “Importar CPT” contém uma tabela com a lista de ensaios importados. A lista serve para selecionar o tipo de ficheiro e o sistema de unidades pretendidos.
| *.txt, *.xlsx, *.csv, *.ods | – | ficheiros de texto ou tabela comuns |
| *.spe | – | formato de dados utilizado na República Checa e Eslováquia, originário do software GeProDo |
| *.cpt | – | ficheiro de texto padrão, particularmente para a Holanda (usado em programas Geodelft M-Serie, por exemplo), que serve para introduzir elevações de pontos individuais e valores de resistência à penetração (pode conter vários CPTs) |
| *.cpt | – | ficheiro de texto Geotech AB CPT |
| *.cpt | – | ficheiro de texto Gouda Geo CPT |
| *.cpt | – | ficheiro de texto Hogentogler CPT |
| *.gef | – | GEF (Geotechnical Exchange Format) é uma estrutura de linguagem geral para armazenar e transferir informação geotécnica Informação detalhada disponível em: https://publicwiki.deltares.nl/display/STREAM/GEF-CPT |
| *.ags | – | formato utilizado para transferir informação geotécnica no Reino Unido Informação detalhada disponível online: http://www.agsdataformat.com/datatransferv4/intro.php |
| *.GRU | – | formato de dados utilizado na Polónia |
O formato TXT permite selecionar um sistema de unidades particular para armazenar os dados do ensaio. Ao importar, o programa converte automaticamente o sistema de unidades adotado para o sistema utilizado pelo programa.
Para uma análise correta, o ensaio deve ser introduzido no subsolo – é necessário introduzir a elevação da superfície original. O ensaio é inserido no subsolo considerando a elevação definida. Se não for definida nenhuma elevação, a origem do ensaio é automaticamente definida como a mesma que a superfície original.
Se utilizar uma certa Norma para o ficheiro de texto do CPT que não esteja incluído no programa, contacte-nos em hotline@fine.cz – será introduzido na versão seguinte.
Caixa de diálogo “Importar (ensaio de penetração de cone)”
Ensaio de Penetração Dinâmica – DPT
O resultado do ensaio de penetração dinâmica (DPT) é o número de pancadas N necessárias para fazer penetrar um instrumento cónico no solo, ou rocha, para um intervalo da profundidade de penetração.
O intervalo da profundidade de penetração difere de acordo com o tipo de sonda de ensaio dinâmico:
![]() DPL – sondagem dinâmica leve
DPL – sondagem dinâmica leve
![]() DPM – sondagem dinâmica média
DPM – sondagem dinâmica média
![]() DPH – sondagem dinâmica pesada
DPH – sondagem dinâmica pesada
![]() DPSH – A – sondagem dinâmica super-pesada
DPSH – A – sondagem dinâmica super-pesada
![]() DPSH – B – sondagem dinâmica super-pesada
DPSH – B – sondagem dinâmica super-pesada
O intervalo da profundidade de penetração é 100 mm para DPL, DPM e DPH e100ou200 mmpara ensaios DPSH- A ou DPSH -B.
O momento de torção necessário para rotacionar 1.5 voltas ou para atingir o valor máximo também deve ser registado, pelo menos após cada 1.0 m de ensaio. Este valor serve para eliminar o atrito de cisalhamento.
Os resultados dos ensaios DPT são apresentados num gráfico. A avaliação dos ensaios DPT são utilizados como parâmetro a introduzir para a modelação estratigráfica do programa “Estratigrafia”.
Os ensaios DPT podem ser importados para o programa como ficheiros .txt.
O nome do ensaio DPT e o deslocamento vertical em relação à origem devem ser introduzidos na caixa de diálogo “Novo ensaio de campo“. No programa “Estratigrafia“, é necessário introduzir as coordenadas x, y, z.
O númro de pancadas e o momento são introduzidos na tabela.
Caixa de diálogo “Novo ensaio de campo”
Bibliografia:
EN ISO 22476-3: Geotechnical investigation and testing – Field testing. Part 2: Dynamic probing test, 2005.
Roy E. Hunt: Geotechnical Engineering Investigation Handbook, Second Edition (CRC Press, 2005)
Ensaio de Sondagem à Percussão (SPT)
O resultado obtido a partir do ensaio de sondagem à percussão (SPT) é o número de pancadas N (resistência à penetração) necessárias para penetrar o dispositivo no solo ou rocha, no intervalo de profundidade de penetração d [m]. O valor deste parâmetro é correntemente assumido como igual a 0.3 m. Este valor pode ser alterado em alguns casos.
O número de pancadas N registado durante o ensaio SPT está correlacionado com a razão de vários instrumentos de teste e com a influência do peso de sobrecargas em areias. O valor corrigido (correlacionado)N60 é utilizado nos cálculos.
O número correlacionado de pancadas N60 é calculado através da seguinte equação:
![]()
| onde: | Er | – | rácio energético do instrumento de teste [%] |
| N | – | número de pancadas registadas durante o ensaio SPT [-/0.3m] | |
| CN | – | correlação para a tensão vertical [–] | |
| λ | – | correlação do usuário [–] |
O rácio energético do instrumento de teste Er[%] representa o rácio entre a energia real Emeas e a energia calculada Etheor do ariete. Não é necessário utilizar a correlação para um instrumento SPT padrão (Mohr), porque a sua eficiência é 60 % e a correlação é realizada para este valor (os valores registados durante a sondagem SPT são utilizados).
A correlação CN para a tensão vertical σ’V representa a influência do peso da sobrecarga em areias. Os valores do fator de correção CN superiores a 1.5 não devem ser utilizados (de acordo com as recomendações de EN ISO 22476-3).
Tabela de tipos de correlações
| Tipo | Tipo de consolidação | Compacidade relativa lp [%] | Fator de correlação CN |
| Tipo 1 – EN ISO 22476-3 (Tab. A2) | Normalmente consolidado | 40 – 60 | |
| Tipo 2 – EN ISO 22476-3 (Tab. A2) | 60 – 80 | ||
| Tipo 3 – EN ISO 22476-3 (Tab. A2) | Sobreconsolidado | – | |
| Tipo 4 – EN ISO 22476-3 | Areias normalmente consolidadas | – | 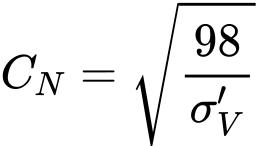 |
| Tipo 5 – FHWA (1998), Peck (1974) | – | – | 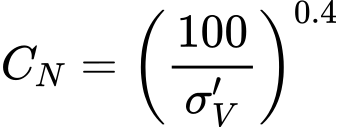 |
| onde: | σ’V | – | tensão vertical efetiva |
A correlação do usuárioλ [–] representa a perda de energia devido ao comprimento do sistema de varões, do impacto do diâmetro do furo ou da influência do instrumento de teste.
Os resultados das sondagens SPT são apresentados num gráfico. A avaliação dos ensaios de penetração são utilizados como parâmetro a introduzir para as análises dos programas “Microestaca” e “Sapata via CPT” e para a modelação estratigráfica do programa “Estratigrafia”.
As sondagens SPT podem ser importados para o programa como ficheiros .txt.
O nome da sondagem SPT e o deslocamento vertical em relação à origem devem ser introduzidos na caixa de diálogo “Novo ensaio de campo“. No programa “Estratigrafia“, é necessário introduzir as coordenadas x, y, z.
O número de pancadas é introduzido na tabela.
Caixa de diálogo “Novo ensaio de campo”
Bibliografia:
EN ISO 22476-3: Geotechnical investigation and testing – Field testing. Part 3: Standard penetration test, 2005.
Roy E. Hunt: Geotechnical Engineering Investigation Handbook, Second Edition (CRC Press, 2005)
Ensaio Pressiométrico (PMT)
O ensaio pressiométrico (PMT) consiste numa sonda pressiométrica colocada no solo testado com adição gradual de água. A dilatação consequente do solo ou rocha em volta do furo é determinada em função do volume de água, com o aumento de pressão que é gradualmente aumentado em intervalos de tempo definidos à priori.
O ensaio pressiométrico fornece os seguintes parâmetros em função da profundidade z [m]:
![]() módulo pressiométrico (Menard)Em [MPa] – obtido a partir do ensaio pressiométrico e depende do tipo de bainha da sonda (manga de borracha, invólucro pré-forrado).
módulo pressiométrico (Menard)Em [MPa] – obtido a partir do ensaio pressiométrico e depende do tipo de bainha da sonda (manga de borracha, invólucro pré-forrado).
![]() pressão limite pLM [MPa] – representa um incremento de pressão hidrostática na sonda de teste, dependente da alteração de volume do solo ou rocha.
pressão limite pLM [MPa] – representa um incremento de pressão hidrostática na sonda de teste, dependente da alteração de volume do solo ou rocha.
Os resultados dos ensaios PMT são apresentados num gráfico. A avaliação dos ensaios pressiométricos (PMT) são utilizados como parâmetro a introduzir para as análises dos programas “Verificação de Contenções”, “Estaca Anti-Deslizante”, “Microestaca” e “Sapata via CPT” e para a modelação estratigráfica do programa “Estratigrafia”.
Os ensaios PMT podem ser importados para o programa como ficheiros .txt.
O nome do ensaio PMT e o deslocamento vertical em relação à origem devem ser introduzidos na caixa de diálogo “Novo ensaio de campo“. No programa “Estratigrafia“, é necessário introduzir as coordenadas x, y, z.
A pressão limite pLM e o módulo de Menard Em são introduzidos na tabela.
Caixa de diálogo “Novo ensaio de campo”
Bibliografia:
EN ISO 22476-4: Geotechnical investigation and testing – Field testing. Part 4: Menard pressuremeter test, 2005.
Roy E. Hunt: Geotechnical Engineering Investigation Handbook, Second Edition (CRC Press, 2005).
Ensaio Dilatométrico (DMT)
O ensaio dilatométrico (DMT) é realizado com recurso a um dilatómetro que opera de acordo com o princípio de verificação de valores ao utilizar os deslocamentos dos sensores indutivos (com uma sensibilidade até 0.001 mm). A vantagem destes ensaios é uma descrição mais exata do deslocamento e deformação do solo de fundação.
 Esquema geral de um ensaio dilatométrico (fonte: [1], Figure 2, pp. 10)
Esquema geral de um ensaio dilatométrico (fonte: [1], Figure 2, pp. 10)
Os resultados dos ensaios DMT são apresentados num gráfico. A avaliação dos ensaios dilatométricos (DMT) são utilizados como parâmetro a introduzir para as análises dos programas “Sapata”, “Verificação de Contenções” e “Estaca Anti-Deslizante” e para a modelação estratigráfica do programa “Estratigrafia”.
Os resultados dos ensaios dilatométricos (DMT) são importados para os programas através de ficheiros em formato UNI (*.uni). É um formato padrão e universal para a importação de dados medidos a partir de ensaios dilatométricos, utilizado em todo o Mundo.
O nome do ensaio DMT e o deslocamento vertical em relação à origem devem ser introduzidos na caixa de diálogo “Novo ensaio de campo“. No programa “Estratigrafia“, é necessário introduzir as coordenadas x, y, z.
O módulo de solo constrangidoMDMT é introduzido na tabela.
 Caixa de diálogo “Novo ensaio de campo”
Caixa de diálogo “Novo ensaio de campo”
Bibliografia:
Marchetti, S., Monaco, P., Totani, G. & Calabrese, M.: The Flat Dilatometer Test (DMT) in soil investigations. A Report by the ISSMGE Committee TC16, University of L’Aquila, Italy, 2001, 48 p.
Roy E. Hunt: Geotechnical Engineering Investigation Handbook, Second Edition (CRC Press, 2005)
EN ISO 22476-11: Geotechnical investigation and testing – Field testing. Part 11: Flat dilatometer test
Análise de Assentamento
Os métodos seguintes estão disponíveis para calcular assentamentos:
![]() Através do módulo edométrico
Através do módulo edométrico
![]() Através da constante de compressão
Através da constante de compressão
![]() Através do índice de compressão
Através do índice de compressão
![]() De acordo com NEN (Buismann, Ladde)
De acordo com NEN (Buismann, Ladde)
![]() Através do modelo de solo mole
Através do modelo de solo mole
![]() De acordo com a teoria de Janbu
De acordo com a teoria de Janbu
![]() Através de DMT (módulo constrangido)
Através de DMT (módulo constrangido)
O programa permite duas opções distintas para restringir a profundidade da zona de influência:
![]() Através da teoria da resistência estrutural
Através da teoria da resistência estrutural
![]() Através da percentagem do valor da tensão geostática
Através da percentagem do valor da tensão geostática
A teoria da elasticidade (teoria de Boussinesq) é utilizada para determinar o estado de tensão no solo em todos os métodos disponíveis para a análise de assentamentos.
De uma forma geral, a teoria do assentamento serva de base a todos os métodos acima mencionados.
Ao computar o assentamento abaixo da base da fundação, o programa começa por calcular a tensão na base da fundação e, seguidamente, determina o assentamento e rotação global da fundação.
A metodologia para todas as teorias consiste na subdivisão do subsolo em camadas com espessuras diferentes, consoante a profundidade abaixo da base da fundação ou da superfície do terreno. A deformação vertical de cada camada é computada – o assentamento global é definido como o somatório dos assentamentos parciais de cada camada dentro da zona de influência (as deformações abaixo da zona de influência são nulas ou desprezadas):
![]()
| onde: | s | – | assentamento |
| si | – | assentamento da iésima camada |
Tensão na Base da Fundação
A tensão na base da fundação pode ser assumida como:
![]() retangular (uniforme na base da fundação)
retangular (uniforme na base da fundação)
![]() geral (trapezoidal) com diferentes valores nas extremidades
geral (trapezoidal) com diferentes valores nas extremidades
A distribuição geral da tensão está demonstrada na figura:
 Tensão na base da fundação
Tensão na base da fundação
onde:
| onde: | Q | – | carregamento vertical da fundação |
| l,b | – | largura e comprimento da fundação | |
| eb | – | excentricidade da carga | |
| M | – | momento atuante na fundação | |
| H | – | força horizontal | |
| N | – | força normal na fundação excêntrica | |
| p | – | distância do eixo do pilar em relação ao centro da fundação |
Se a tensão for negativa em algum ponto, o programa prossegue com dimensões ajustadas b*l enquanto que exclui a tensão da análise. Antes de computar a distribuição da tensão devido à sobrecarga, a tensão na base da fundação é reduzida pela tensão geostática, da seguinte forma:
![]()
O programa permite três opções diferentes para especificar a tensão geostática na base da fundação:
![]() A partir da superfície do terreno original – é considerado que a profundidade da base da fundação no poço a céu aberto é medida a partir da superfície do terreno original e que não está tensionada por um período de tempo inferior ao necessário para que se verifique um aumento de volume do solo e consequente perda de tensão no subsolo.
A partir da superfície do terreno original – é considerado que a profundidade da base da fundação no poço a céu aberto é medida a partir da superfície do terreno original e que não está tensionada por um período de tempo inferior ao necessário para que se verifique um aumento de volume do solo e consequente perda de tensão no subsolo.
![]() A partir da superfície do terreno final – São aplicadas as mesmas suposições que as descritas acima.
A partir da superfície do terreno final – São aplicadas as mesmas suposições que as descritas acima.
![]() Não considerada.
Não considerada.
Assentamento e Rotação Globais da Fundação
O assentamento da fundação é influenciado pela rigidez global do sistema, representado pela estrutura da fundação e pelo solo da fundação, dado por:
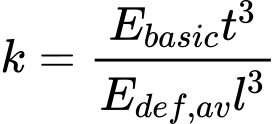
| onde: | Ebasic | – | módulo de elasticidade da fundação |
| t | – | espessura da fundação | |
| Edef, av | – | média ponderada do módulo de deformação até à profundidade da zona de influência | |
| l | – | dimensão da fundação na direção da rigidez em análise |
Para k > 1, a fundação é assumida como rígida e é assumido como ponto representativo do assentamento o ponto característico (dista do seu eixo 0.37 vezes a dimensão da fundação).
Para k < 1, a estrutura da fundação é assumida como compatível e é assumido como ponto representativo do assentamento o ponto central da fundação.
A rotação da fundação é determinada a partir da diferença de assentamentos de cada centro das extremidades.
 Rotação da sapata – princípio de cálculo
Rotação da sapata – princípio de cálculo
Influência da Profundidade da Fundação e do Subsolo Incompressível
Ao computar o assentamento, é possível considerar a influência da profundidade da fundação ao introduzir o coeficiente de redução κ1:
para sapatas contínuas:
![]()
para sapatas isoladas:
![]()
| onde: | d | – | profundidade da base da fundação |
| z | – | profundidade abaixo da base da fundação |
A influência da camada incompressível é introduzida na análise através do coeficiente κ2:
![]()
| onde: | zic | – | profundidade da base rígida abaixo da base da fundação |
| z | – | profundidade abaixo da base da fundação |
A incorporação destes coeficientes permite a transformação da componente vertical da tensão σz de forma a que a profundidade real seja substituída por um valor substituto zr, dado por:
![]()
| onde: | κ1 | – | coeficiente da profundidade da base da fundação |
| κ2 | – | coeficiente da base rígida | |
| z | – | profundidade abaixo da base da fundação |
Influência da Almofada Areia-Cascalho
Se for introduzido uma almofada areia-cascalho abaixo da fundação, os parâmetros materiais X de cada camada são computados da seguinte forma:
Para a camada ha,i:
![]()
| onde: | Xi | – | parâmetro material da iésima camada |
| Xc | – | parâmetro material da almofada cascalho-areia |
Para a camada hb,i:
![]()
![]()
| onde: | Ac | – | área da almofada areia-cascalho |
| Xc | – | parâmetro material da almofada cascalho-areia | |
| Xb,i | – | parâmetro material da b,i camada | |
| bi | – | largura da almofada na iésima camada | |
| li | – | comprimento da almofada na iésima camada |
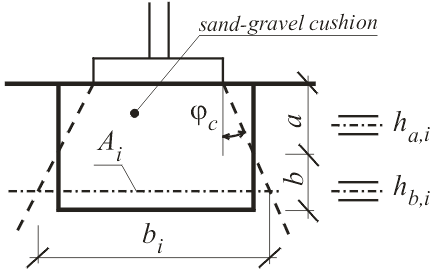 Análise de Xi na almofada areia-cascalho
Análise de Xi na almofada areia-cascalho
Análise através do Módulo Edométrico
A equação para computar a compressão na iésima camada do solo abaixo da fundação, com uma espessura h, é obtida a partir da definição do módulo edométrico Eoed:
![]()
| onde: | σz,i | – | componente vertical do aumento de tensão no centro da iésima camada |
| hi | – | espessura da iésima camada | |
| Eoed,i | – | módulo edométrico da iésima camada |
O módulo edométrico Eoed pode ser especificado para cado solo como uma constante ou através de uma curva edométrica (relação σef/ε). Ao utilizar a curva edométrica, o programa assume, para cada camada, o valor correspondente de Eoed para um intervalo entre a tensão original e final. Se o valor do módulo edométrico Eoed não estiver disponível, é possível introduzir o módulo de deformação Edef e o programa prossegue com o ajuste respetivo.
![]()
onde:
![]()
| onde: | ν | – | coeficiente de Poisson |
| Edef | – | módulo de deformação |
Análise através da Constante de Compressão
A equação utilizada para computar a compressão da iésima camada de solo abaixo da fundação, com espessura h, depende da constante de compressão C:
![]()
| onde: | σor,i | – | componente vertical da tensão geostática original no centro da iésima camada |
| σz,i | – | componente vertical do aumento de tensão (ex.: tensão devido à sobrecarga da estrutura) que induz a compressão da camada | |
| hi | – | espessura da iésima camada | |
| Ci | – | constante de compressão na iésima camada |
O programa permite introduzir a constante de compressão Ci ou a constante de compressão C10 (o programa executa a transformação automaticamente).
Análise através do Índice de Compressão
A equação para calcular o assentamento, considerando o índice de compressão Cc da iésima camada, é a seguinte:
![]()
| onde: | σor,i | – | componente vertical da tensão geostática no centro da iésima camada |
| σz,i | – | componente vertical do aumento de tensão (ex.: tensão devido à sobrecarga da estrutura) induzida na camada de compressão | |
| eo | – | índice de vazios inicial | |
| hi | – | espessura da iésima camada | |
| Cc,i | – | índice de compressão da iésima camada |
Análise de acordo com NEN (Buismann, Ladd)
Este método computa o assentamento primário e secundário. Ao computar, o método considera solos sobreconsolidados e faz a distinção entre dois casos possíveis:
![]() A soma da tensão vertical efetiva no solo com a tensão devido a uma sobrecarga externa é inferior à pressão pré-consolidada, sendo que apenas a sobrecarga adicional é considerada.
A soma da tensão vertical efetiva no solo com a tensão devido a uma sobrecarga externa é inferior à pressão pré-consolidada, sendo que apenas a sobrecarga adicional é considerada.
![]() A soma da tensão vertical efetiva no solo com a tensão devido a uma sobrecarga externa é superior à pressão pré-consolidada, sendo a consolidação primário considerada novamente. O assentamento primário deste caso é superior ao do caso anterior.
A soma da tensão vertical efetiva no solo com a tensão devido a uma sobrecarga externa é superior à pressão pré-consolidada, sendo a consolidação primário considerada novamente. O assentamento primário deste caso é superior ao do caso anterior.
Assentamento primário
O assentamento primário da iésima camada de solo sobreconsolidado (OCR > 1) é dado por:
para: σor+ σz ≤ σp (a soma da tensão vertical e do seu incremento é inferior à pressão de pré-consolidação):
![]()
para: σor+ σz > σp (a soma da tensão vertical e do seu incremento é superior à pressão de pré-consolidação):
![]()
| onde: | σor,i | – | componente vertical da tensão geostática no centro da iésima camada |
| σz,i | – | componente vertical do aumento de tensão (ex.: tensão devido à sobrecarga da estrutura) induzida na camada de compressão | |
| σp,i | – | pressão de pré-consolidação na iésima camada | |
| eo | – | índice de vazios inicial | |
| hi | – | espessura da iésima camada | |
| Cc,i | – | índice de compressão da iésima camada | |
| Cr,i | – | índice de recompressão da iésima camada |
O assentamento primário da iésima camada de solo normalmente consolidado (OCR = 1) é dado por:
![]()
| onde: | σor,i | – | componente vertical da tensão geostática no centro da iésima camada |
| σz,i | – | componente vertical do aumento de tensão (ex.: tensão devido à sobrecarga da estrutura) induzida na camada de compressão | |
| eo | – | índice de vazios inicial | |
| hi | – | espessura da iésima camada | |
| Cc,i | – | índice de compressão da iésima camada |
Assentamento secundário
O assentamento secundário da iésima camada é dado por:
para: σor+ σz ≤ σp (a soma da tensão vertical e do seu incremento é inferior à pressão de pré-consolidação):
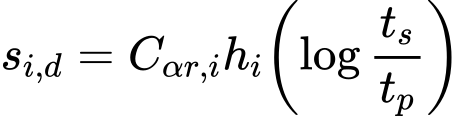
para: σor+ σz > σp (a soma da tensão vertical e do seu incremento é superior à pressão de pré-consolidação):
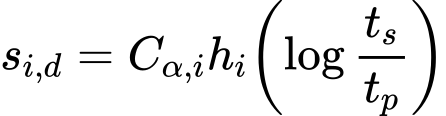
| onde: | hi | – | espessura da iésima camada |
| Cαr,i | – | índice de compressão secundária abaixo da pressão de pré-consolidação na iésima camada | |
| Cα | – | índice de compressão secundária na iésima camada | |
| tp | – | tempo para terminar a consolidação primária | |
| ts | – | tempo necessário para o assentamento secundário |
Se o valor do índice de pré-consolidação da compressão secundária for igual ao valor do índice de compressão secundária, o programa não considera o efeito da pressão de pré-consolidação na computação do assentamento secundário.
Bibliografia:
Netherlandish standard NEN6740, 1991, Geotechniek TGB1990 Basisen en belastingen, Nederlands normalisatie-Institut.
Análise através do Modelo de Solo Mole
A análise aplica o índice de compressão modificado λ e baseia-se no modelo de solo elasto-plástico mole, desenvolvido na Universidade de Cambridge. A deformação do solo assume uma tensão volumétrica linearmente dependente da alteração da tensão efetiva média ε, esboçada numa escala logarítmica natural. O assentamento na iésima camada é dado por:
![]()
| onde: | σor,i | – | componente vertical da tensão geostática no centro da iésima camada |
| σz,i | – | componente vertical do aumento de tensão (ex.: tensão devido à sobrecarga da estrutura) induzida na camada de compressão | |
| hi | – | espessura da iésima camada | |
| λ | – | índice de compressão modificado da iésima camada |
A análise implica a introdução do índice de compressão modificado λ que é, normalmente, obtido a partir de ensaios laboratoriais triaxiais.
Se o índice de compressão modificado λ for conhecido, é possível especificar o índice de compressão CC juntamente com um valor médio do volume de vazios e (se não for conhecido, é suficiente introduzir o volume de vazios inicial eo) e o programa realizar uma computação aproximada do índice de compressão modificado λ a partir dos dados disponíveis.
Bibliografia:
Burland J.B. The yielding and dilatation of clay (correspondence), Géotechnique, 15 (2),1965, str. 211-214.
Análise de acordo com a Teoria de Janbu
Baseia-se nos princípios da deformação elástica não linear, em que a relação tensão-deformação é descrita por uma função de dois parâmetros adimensionais únicos para um dado solo. Os parâmetros são o expoente j e o módulo de Janbu m. As equações que descrevem o assentamento são obtidas através da definição de ε a partir do módulo Et e da integração consequente. O programa permite que o usuário compute o assentamento para os seguintes tipos de solo:
![]() Solos não coesivos
Solos não coesivos
![]() Solos com graduação grossa
Solos com graduação grossa
![]() Areias e siltes
Areias e siltes
![]() Areias e siltes sobreconsolidados
Areias e siltes sobreconsolidados
![]() Solos coesivos
Solos coesivos
![]() Solos coesivos sobreconsolidados
Solos coesivos sobreconsolidados
Bibliografia:
Method of settlement computation for various types of soils, Soil Mechanics and foundation engineering, Springer, 7 (3), 1970, str, 201-206.
Análise para Solos Não Coesivos
Para solos não coesivos, o expoente da tensão é diferente de zero. Para subsolos em camadas, o assentamento resultante é igual ao somatório dos assentamentos parciais de cada camada:
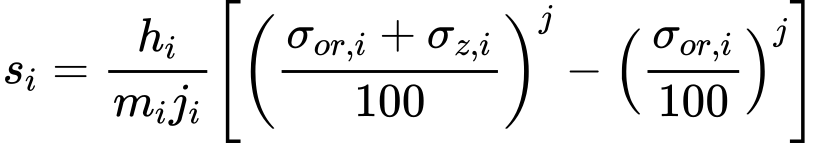
| onde: | σor,i | – | componente vertical da tensão geostática no centro da iésima camada |
| σz,i | – | componente vertical do aumento de tensão (ex.: tensão devido à sobrecarga da estrutura) induzida na camada de compressão | |
| ji | – | expoente da tensão na iésima camada | |
| mi | – | módulo de Janbu iésima camada | |
| hi | – | espessura da iésima camada |
Análise para Solos de Graduação Grossa
Para solos de graduação grossa (ex.: solo gelado), a relação tensão-deformação (assentamento) é assumida como elástica, isto é, o expoente da tensão j é igual a um. Então, para j = 1 e para a tensão de referência σr = 100 kPa, o assentamento resultante é igual ao somatório dos assentamentos parciais de cada camada:
![]()
| onde: | σz,i | – | componente vertical do aumento de tensão (ex.: devido a uma sobrecarga da estrutura) induzida na camada comprimida – isto é, variação da tensão efetiva |
| mi | – | módulo de Janbu iésima camada | |
| hi | – | espessura da iésima camada |
Análise para Areias e Siltes
Para areias e siltes, o expoente da tensão j assume um valor de, aproximadamente, 0.5, para a tensão de referência de σr = 100 kPa, com o assentamento resultante a ser igual ao sumatório dos assentamentos parciais de cada camada. Os assentamentos parciais podem ser calculados através da seguinte fórmula:
![]()
| onde: | σor,i | componente vertical da tensão geostática no centro da iésima camada |
| σz,i | componente vertical do aumento de tensão (ex.: tensão devido à sobrecarga da estrutura) induzida na camada de compressão | |
| mi | módulo de Janbu iésima camada | |
| hi | espessura da iésima camada |
Análise para Areias e Siltes Sobreconsolidados
Se a tensão final do solo exceder a pressão de pré-consolidação (σor+ σz > σp), o assentamento do subsolo em camadas é dado pela seguinte equação:
![]()
| onde: | σor,i | – | componente vertical da tensão geostática no centro da iésima camada |
| σp,i | – | pressão de pré-consolidação na iésima camada | |
| σz,i | – | componente vertical do aumento de tensão (ex.: tensão devido à sobrecarga da estrutura) induzida na camada de compressão | |
| mi | – | módulo de Janbu iésima camada | |
| mr,i | – | módulo de recompressão de Janbu da iésima camada | |
| hi | – | espessura da iésima camada |
Se a tensão devido a uma sobrecarga não implicar que a tensão final exceda a pressão de pré-consolidação (σor+ σz ≤ σp), é possível assumir a seguinte forma para a equação de cálculo do assentamento parcial de cada camada de areia ou silte do subsolo:
![]()
| onde: | σor,i | – | componente vertical da tensão geostática no centro da iésima camada |
| σp,i | – | pressão de pré-consolidação na iésima camada | |
| σz,i | – | componente vertical do aumento de tensão (ex.: tensão devido à sobrecarga da estrutura) induzida na camada de compressão | |
| mr,i | – | módulo de compressão de Janbu da iésima camada | |
| hi | – | espessura da iésima camada |
Análise para Solos Coesivos
No caso de solos coesivos, o expoente da tensão é igual a zero. Para solos normalmente consolidados, A equação para o cálculo do assentamento em subsolos por camadas formadas por solos coesivos, é definida a partir do módulo tangente de deformação (por modificação e consequente integração) Et:
![]()
| onde: | σor,i | – | componente vertical da tensão geostática no centro da iésima camada |
| σz,i | – | componente vertical do aumento de tensão (ex.: tensão devido à sobrecarga da estrutura) induzida na camada de compressão | |
| mi | – | módulo de Janbu iésima camada | |
| hi | – | espessura da iésima camada |
Análise para Solos Coesivos Sobreconsolidados
A maioria dos solos coesivos, na sua forma original e exceto argilas muito recentes ou orgânicas, são sobreconsolidados. Se a tensão final no solo exceder a tensão sobreconsolidada (σor+ σz > σp), então o assentamento do subsolo em camadas compostas por solos coesivos é dado por:
para: σor+ σz > σp
![]()
para: σor+ σz ≤ σp
![]()
| onde: | σor,i | – | componente vertical da tensão geostática no centro da iésima camada |
| σp,i | – | pressão de pré-consolidação na iésima camada | |
| σz,i | – | componente vertical do aumento de tensão (ex.: tensão devido à sobrecarga da estrutura) induzida na camada de compressão | |
| mi | – | módulo de Janbu iésima camada | |
| mr,i | – | módulo de recompressão de Janbu na iésima camada | |
| hi | – | espessura da iésima camada |
Análise de Assentamento através de DMT (Módulo de Solo Constrangido)
O módulo constrangido MDMT é definido como o módulo confinado drenado tangente vertical de σvo. O módulo MDMT é obtido a partir de ensaios dilatométricos (DMT).
Se o valor do módulo constrangido MDMT não estiver disponível, é possível inserir o coeficiente de compressibilidade de volume mV (determinado a partir de ensaios edométricos) e o programa realiza a adaptação necessária:
![]()
| onde: | MDMT | – | módulo constrangido |
| mV | – | coeficiente de compressibilidade volumétrica |
A análise aplica o módulo constrangido MDMT ou o coeficiente de compressibilidade de volume mV e baseia-se na teoria de Marchetti. Este método baseado na elasticidade linear, fornece um assentamento proporcional à carga, não sendo possível obter estimativas não lineares.
O assentamento da iésima camada é dada:
![]()
| onde: | σz,i | – | componente vertical do incremento da tensão na iésima camada |
| hi | – | espessura da iésima camada | |
| MDMT | – | módulo constrangido |
Bibliografia:
Marchetti, S., Monaco, P., Totani, G. & Calabrese, M.: The Flat Dilatometric Test (DMT) in soil investigations. A Report by the ISSMGE Committee TC16, University of L’Aquila, Italy, 2001, 48 p.
Teoria do Assentamento
Se se verificarem alterações da tensão no solo ou na estrutura, devido a sobrecargas superficiais, é possível determinar a deformação do solo. A deformação do solo é, geralmente, inclinada e a sua componente vertical é definida como o assentamento. Em geral, os assentamentos são não estacionários e dependentes do tempo, o que significa que não acontecem imediatamente após a introdução da sobrecarga, mas que dependem das características de consolidação do solo. Solos permeáveis e com menor compressibilidade (areia, cascalho) sofrem deformações rapidamente, enquanto que solos argilosos com pouca permeabilidade sofrem deformações graduais, conhecidas como consolidação.
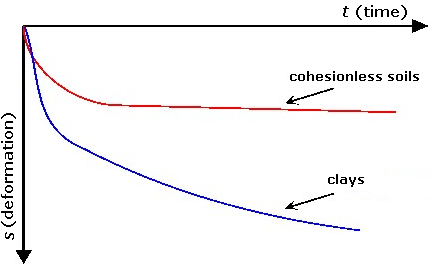 Assentamento dos solos em função do tempo
Assentamento dos solos em função do tempo
As cargas aplicadas originam assentamentos que podem ser subdivididos consoante a sua resposta temporal, em três componentes diferentes:
![]() Assentamento instantâneo (inicial)
Assentamento instantâneo (inicial)
![]() Assentamento primário (consolidação)
Assentamento primário (consolidação)
![]() Assentamento secundário (depressão)
Assentamento secundário (depressão)
Assentamento instantâneo
Durante o assentamento instantâneo, o solo apenas experimenta deformações de cisalhamento resultantes da variação de forma de forma sem deformação volumétrica. A perda de pressão nos poros do solo é nula.
Assentamento primário
Esta fase da deformação do solo é caracterizada por deformação do esqueleto devido ao movimento e compressão de partículas provocados por variações de volume. Se os poros estiverem preenchidos com água (especialmente no caso de solos com pouca permeabilidade), a água será transportada desde poros espremidos para locais com menor pressão (o solo será alvo de consolidação). O assentamento por consolidação primária é dependente do tempo e termina ao atingir o ponto de pressão nos poros nulo.
Assentamento secundário
Quando a consolidação primária termina, a deformação do esqueleto deixa de alterar a pressão nos poros (teoricamente, para um tempo infinito). Com o aumento da pressão, as partículas podem ficar tão comprimidas que se podem deformar entre elas próprias e o volume continua a variar – este processo é conhecido como deformação por depressão do esqueleto ou consolidação (assentamento) secundária. Ao contrário da consolidação primária, a consolidação secundária dá-se sob o efeito de tensão efetiva constante. Particularmente no caso de solos moles plásticos ou espremidos, a consolidação secundária não deve ser desprezada – no caso de solos sobreconsolidados, pode representar cerca de 10% do assentamento total e para solos normalmente consolidados pode chegar a cerca de 20%.
Assentamento Primário
O assentamento primário final s é muitas vezes substituído pelo termo assentamento. A maioria dos métodos computacionais pode ser englobada em um destes dois grupos:
![]() Deformação elástica linear
Deformação elástica linear
![]() Deformação elástica não linear
Deformação elástica não linear
Deformação elástica linear
A relação tensão-deformação é dada pela lei de Hook:
![]()
| onde: | ε | – | deformação induzida da camada do solo |
| Δσef | – | variação induzida na tensão efetiva na camada do solo | |
| E | – | módulo de Young na camada | |
| ν | – | coeficiente de Poisson |
A aplicabilidade do módulo de Young E da elasticidade é fundamentada apenas em casos em que o solo tensionado pode expandir-se na direção horizontal. No entanto, apenas é aceitável para pequenas fundações contínuas. Ao aplicar a carga sobre um área maior, o solo tensionado não se deforma lateralmente, exceto nas extremidades, e experimenta apenas uma deformação vertical (unidimensional) relacionada com o módulo edométrico Eoed, que é superior ao módulo E.
O assentamento de uma camada do solo s é determinada a partir da deformação da camada do solo ε pela espessura da camada (altura) Ho:
![]()
| onde: | ε | – | deformação induzida da camada do solo |
| Ho | – | espessura da camada |
No caso de subsolos em camadas, o assentamento total é obtido a partir do somatório dos assentamentos de cada camada:
![]()
| onde: | s | – | assentamento do subsolo em camadas |
| εi | – | deformação da iésima camada | |
| Hoi | – | espessura da iésima camada |
Deformação elástica não linear
Para a maioria dos solos, a relação tensão-deformação é não linear e muitas vezes influenciada pelo histórico do carregamento. Esta não linearidade não pode ser desprezada, particularmente ao computar o assentamento de solos de graduação fina (siltes, argilas). O procedimento baseado na aplicação do módulo de Young da elasticidade não é, geralmente, aplicável. Mesmo ao aplicar a tensão dependente do módulo edométrico de deformação, não será possível obter estimativas razoáveis do comportamento de certos solos sobreconsolidados. A deformação elástica não linear é modelada através do índice de vazios e as características da deformação são derivadas da deformação unidimensional de uma amostra de solo (ex.: constante de compressão, índice de compressão, etc.).
O procedimento para a computação do assentamento de um solo saturado compressível através do índice de vazios e é demonstrado a partir do elemento de solo seguinte, com altura Ho e largura B = 1 m:
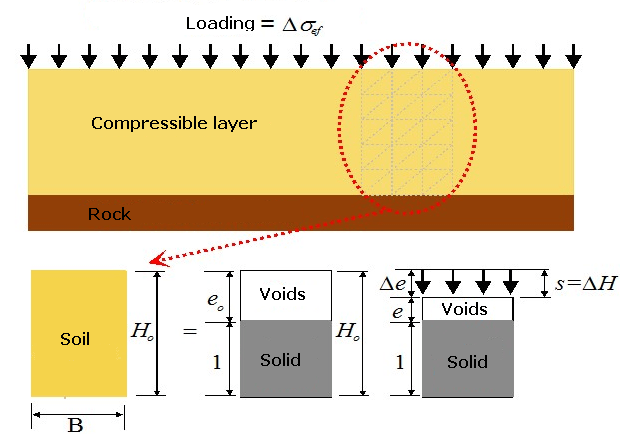 Análise de assentamento a partir de diagrapa de fase
Análise de assentamento a partir de diagrapa de fase
Devido ao facto de que o solo é um meio trifásico (contém partículas sólidas e poros preenchidos com fluídos e gases), é possível descrever as partículas do solo (partículas de rochas e grãos minerais) pelo seu volume Vs (e assumi-lo como igual a um), enquanto que a fase porosa pode ser descrita pelo índice de vazios e.
O elemento do solo está sujeito, na sua superfície superior, a uma carga uniforme q, que causa uma variação de tensão no interior da amostra e no deslocamento vertical ΔH, que leva a uma redução dos poros Vp e, consequentemente, à redução do índice de vazios (desde o seu valor original eo até ao seu novo valor e). A deformação vertical ε de uma amostra de solo é dada pelo rácio de ΔH até à sua altura original Ho e pode ser exprimida através do índice de vazios e:
![]()
| onde: | ε | – | compressão vertical relativa |
| ΔH | – | deformação vertical | |
| Ho | – | altura original do elemento | |
| s | – | assentamento | |
| e | – | índice de vazios | |
| Δe | – | variação do índice de vazios |
Ao modificar esta equação, é possível obter a fórmula que descreve o assentamento da amostra através do índice de vazios:
![]()
| onde: | ε | – | compressão vertical relativa |
| Ho | – | altura original do elemento | |
| s | – | assentamento | |
| e | – | índice de vazios | |
| Δe | – | variação do índice de vazios |
Assentamento Secundário
Para descrever a deformação gradual do solo durante o assentamento secundário, o programa aplica o método de Buissman (incorpora o índice de compressão secundária Cα segundo Ladd). A partir de observações que sugerem que a deformação do solo apresenta uma curva linear para uma escala semi-logarítmica em função do tempo, Buissman propôs que a variação de ε devido a tensões a longo termo seja dada por:
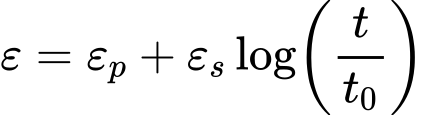
| onde: | ε | – | deformação total |
| εp | – | deformação associada à consolidação primária | |
| εs | – | deformação associada à consolidação secundária | |
| t | – | tempo de consolidação | |
| t0 | – | tempo de referência |
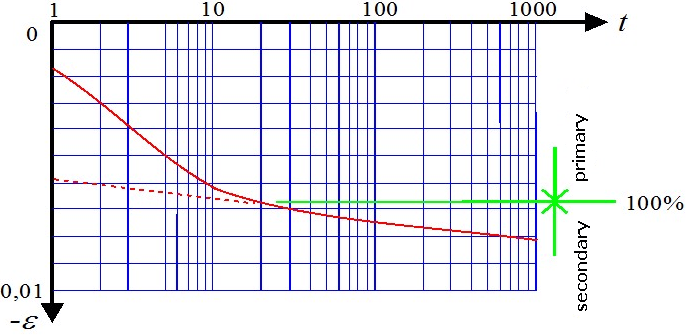 Deformação em função do tempo (consolidação primária e secundária)
Deformação em função do tempo (consolidação primária e secundária)
Análise de Consolidação
O programa permite a análise da consolidação quando esta é ativada na janela “Configurações”. Camadas consolidadas formadas por solos impermeáveis, assentam com o passar do tempo. A consolidação afeta os valores da pressão nos poros. Os parâmetros do solo que influenciam a análise de consolidação são definidos na janela “Solos”, os outros parâmetros de consolidação são definidos na janela “Análises” para cada etapa de construção.
O coeficiente de consolidação, dependente das propriedades do solo, é dado por:
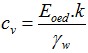
| onde: | Eoed | – | módulo oedomeétrico da deformação |
| k | – | coeficiente de permeabilidade | |
| γw | – | peso volúmico da água |
Quando a camada consolidada é composta por solos não homogêneos, o coeficiente cv é avaliado como a média dos coeficientes do solo.
A análise de consolidação também é influenciada por fatores de tempo, que dependem do fluxo de água. Este fluxo é igual à espessura da camada consolidada, caso o fluxo se verifique em apenas uma direção (ascendente ou descendente) ou para metade da camada, caso o fluxo se verifique em ambas as direções (ascendente e descendente). O fator de tempo real é dado pela seguinte fórmula:
![]()
| onde: | cv | – | coeficiente de consolidação |
| t | – | tempo real | |
| H | – | fluxo de drenagem |
O fator de tempo da duração da construção é influenciado pela duração da ação do carregamento. Quando o carregamento total é introduzido no início da etapa, o tempo de construção é zero. Quando o carregamento aumenta linearmente durante a duração da etapa, o tempo de construção é igual ao tempo de duração da etapa. O fator de tempo da duração da construção é dado por:
![]()
| onde: | cv | – | coeficiente de consolidação |
| tc | – | tempo de construção | |
| H | – | fluxo de drenagem |
O nível de consolidação é avaliado a partir das seguintes fórmulas:
| para: | 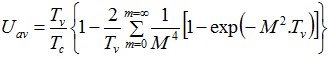 | |
| para: | 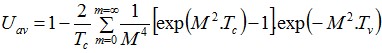 | |
| onde: |
| onde: | Tv | – | fator de tempo real |
| Tc | – | fator de tempo de construção |
O valor original da deformação na camada consolidada, numa dada etapa da construção, é multiplicado pelo nível de consolidação Uav correspondente, de modo a obter o valor da deformação:
![]()
| onde: | εfin | – | valor final da deformação |
| ε | – | valor original da deformação | |
| Uav | – | nível de consolidação |
A análise de consolidação também influencia os valores da pressão nos poros em camadas consolidadas. Quando se introduz a ação do carregamento, os valores da pressão nos poros são os mais elevados. Com o passar do tempo, a tender para infinito, a pressão dos poros tende a decrescer até zero.
Pressão nos poros:
| para: | 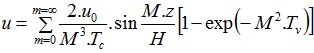 | |
| para: | 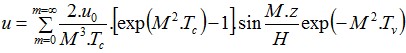 | |
| onde: |
| onde: | Tv | – | fator de tempo real |
| Tc | – | fator de tempo de construção | |
| H | – | fluxo de drenagem | |
| z | – | profundidade do ponto onde a pressão nos poros é avaliada | |
| u0 | – | variação da tensão efetiva comparativamente à etapa anterior (carga) |
Bibliografia:
Braja M. Das. Advanced Soil Mechanics; Taylor & Francis: London, 2008.pp278 – 316Verruijt A. Soil Mechanics, Delft University of Technology, 2010, pp97-123.
http://geo.verruijt.net/software/SoilMechBook.pdf.
Determinação da Profundidade da Zona de Influência
A partir de um ponto de vista teórico, ao aplicar uma carga na superfície do terreno é expectável a alteração da tensão no subsolo até um profundidade infinita. No entanto, o solo sobre deformações apenas até uma certa profundidade – dentro da zona de influência.
O programa oferece duas opções para especificar a zona de influência:
![]() Através da teoria da resistência estrutural
Através da teoria da resistência estrutural
![]() Através da especificação de uma certa percentagem da tensão geostática primária
Através da especificação de uma certa percentagem da tensão geostática primária
Teoria da Resistência Estrutural
A resistência estrutural representa a resistência do solo contra a deformação provocada por uma carga que dê origem à rotura da sua estrutura interna. Com a diminuição do coeficiente m, a resposta do solo tende a ser linear.
Se a resistência estrutural for considerada durante a análise de assentamento, então:
a) a zona de influência é caracterizada pela profundidade sob a base da fundação, onde o aumento da tensão vertical σz se torna igual à resistência estrutural do solo (determinada pela multiplicação da tensão geostática original σor pelo coeficiente m):
![]()
| onde: | m | – | coeficiente de resistência estrutural |
| σor | – | tensão geostática original |
b) ao computar o assentamento da camada, o aumento da tensão vertical σz devido a uma sobrecarga e é reduzido pela resistência estrutural do solo, é dado por:
![]()
| onde: | m | – | coeficiente de resistência estrutural |
| σor | – | tensão geostática original | |
| σz | – | aumento de tensão no centro da camada |
e o assentamento s é calculado consoante tensão, conforme mostra a figura, e é dado por:
![]()
| onde: | m | – | coeficiente de resistência estrutural |
| σor | – | tensão geostática original | |
| σz | – | aumento de tensão no centro da camada |
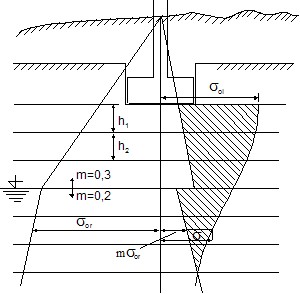 Profundidade da zona de influência com base na teoria da resistência estrutural
Profundidade da zona de influência com base na teoria da resistência estrutural
Método da Restrição do Valor da Tensão Primária
Se se assumir, na análise de assentamento, os constrangimentos em termos de percentagem da tensão geostática primária, então:
a) a zona de influência é representada pela profundidade abaixo da base da fundação, onde o aumento de tensão σz atinge uma certa percentagem da tensão geostática original:
![]()
| onde: | x% | – | valor da tensão geostática considerado |
| σo | – | tensão geostática |
b) o assentamento s é derivado do valor da tensão, conforme mostra a figura, e apresenta a forma seguinte:
![]()
| onde: | σz | – | aumento de tensão |
| σor | – | tensão geostática |
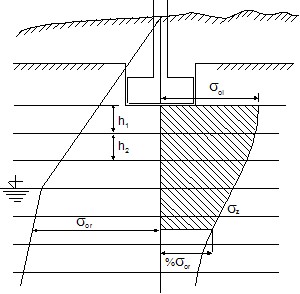 Profundidade da zona de influência com base na restrição do valor da tensão primária
Profundidade da zona de influência com base na restrição do valor da tensão primária
Características da Análise de Assentamento
Dependendo do método selecionado, o programa aplica as seguintes características para a computação do assentamento, que podem diferir no tipo de ensaio necessário para a sua determinação ou na forma de representação das variáveis medidas:
![]() Índice de compressão Cc
Índice de compressão Cc
![]() Módulo edométrico Eoed
Módulo edométrico Eoed
![]() Módulo de deformação Edef
Módulo de deformação Edef
![]() Constante de compressão C
Constante de compressão C
![]() Constante de compressão 10 C10
Constante de compressão 10 C10
![]() Índice de vazios e
Índice de vazios e
![]() Índice de recompressão Cr
Índice de recompressão Cr
![]() Características de Janbu
Características de Janbu
![]() Coeficiente de correção m
Coeficiente de correção m
![]() Índice de compressão modificado λ
Índice de compressão modificado λ
![]() Índice de compressão secundária Cα
Índice de compressão secundária Cα
![]() Índice de sobreconsolidação da compressão secundária Cαr
Índice de sobreconsolidação da compressão secundária Cαr
Índice de Compressão
Descreve a variação do índicie de vazios e em função da variação da tensão efetiva σef, para uma escala logarítmica:
 Índice de vazios e versus tensão efetiva σef
Índice de vazios e versus tensão efetiva σef
Representa a deformação característica de solos sobreconsolidados:
![]()
| onde: | Δe | – | variação do índice de vazios |
| Δlogσef | – | variação da tensão efetiva |
Intervalo do índice de compressão Cc (Naval Facilities Engineering Command Soil MechanicsDESIGN MANUAL 7.01)
Um intervalo típico para o índice de compressão é entre 0.1 a 10. Os valores aproximados para areia, para uma escala de carregamento entre 95 kPa e 3926 kPa , vão desde 0.05 a 0.06 para areias soltas e 0.02 a 0.03 para areias densas. O valor para siltes é 0.20.
Para argilas e siltes ligeiramente consolidados, testados por Kaufmann e Shermann (1964), em Louisiana, EUA, apresentam-se os valores seguintes:
| Solo | Tensão de consolidação efetiva σcef [kPa] | Tensão efetiva final no solo σef [kPa] | Índice de compressão Cc [-] |
| Argila mole CL | 160 | 200 | 0.34 |
| Argila dura CL | 170 | 250 | 0.44 |
| Silte ML de baixa plasticidade | 230 | 350 | 0.16 |
| Argila CH de alta plasticidade | 280 | 350 | 0.84 |
| Argila mole CH com camadas de silte | 340 | 290 | 0.52 |
O Prof. Juan M.Pestana-Nascimento (University of California, Berkeley) propôs os seguintes valores para o índice de compressão Cc:
| Solo | Índice de compressão Cc [-] |
| Argilas normalmente consolidadas | 0.20 – 0.50 |
| Argila de Chicago com silte (CL) | 0.15 – 0.30 |
| Argila azul da Boston (CL) | 0.30 – 0.50 |
| Argila de Vicksburg (CH) | 0.3 – 0.6 |
| Argila da Suécia (CL – CH) | 1 – 3 |
| Argila de Leda, Canadá (CL – CH) | 1 – 4 |
| Argila da Cidade do México (MH) | 7 – 10 |
| Argilas orgânicas (OH) | 4 ou mais |
| Turfa (Pt) | 10 – 15 |
| Siltes orgânicos e siltes argilosos (ML – MH) | 1.5 – 4.0 |
| Sedimentos de São Francisco (CL) | 0.4 – 1.2 |
| Argila da baía velha de São Francisco | 0.7 – 0.9 |
| Argila da Bangcoque (CH) | 0.4 |
Existem expressões empíricas para a determinação de valores aproximados de Cc para siltes, argilas e solos orgânicos; no entanto, a sua aplicabilidade é, mais ou menos, local:
| Solo | Equações | Referência |
| Argilas transformadas | Skempton 1944 | |
| Argilas | Nishida 1956 | |
Argilas do Brasil Argiras de São Paulo |
| Cozzolino 1961 |
| Argilas de Nova Iorque | Terzaghi a Peck 1948 | |
| Argilas de baixa plasticidade | Sowers 1970 | |
| Argilas e siltes de Taipei |
| Moh a kol. 1989 |
| Argilas |
| Pestana 1994 |
Módulo Edométrico
Se os resultados do ensaio edométrico estiverem representados através da curva edométrica (Δε = f(Δσef )), torna-se evidente que para cada ponto da curva existe um rácio σef /ε diferente.
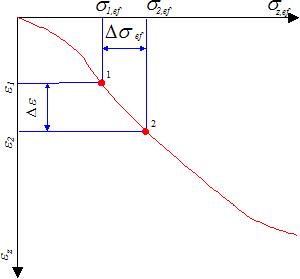 Determinação do módulo edométrico Eoed
Determinação do módulo edométrico Eoed
Se a curva tensão-deformação para um certo intervalo de duas tensões vizinhas σ1ef – σ2ef for substituída por uma linha secante, é aceitável assumir um comportamento do solo linear, dentro deste intervalo, e representar a compressibilidade do solo como Δσef/Δε – denominado módulo edométrico de deformação. O módulo edométrico de deformação é o módulo secante ligado a um dado intervalo de tensões σ1ef – σ2ef selecionado a partir do diagrama tensão-deformação Δε = (Δσef):
![]()
Em geral, o módulo edométrico de deformação Eoed tende a diminuir com o aumento do valor do intervalo de intensões. É necessário considerar, para cada camada, uma valor específico de Eoed, adequado a cada intervalo de tensões (do estado de tensão original ao final). Isto é considerado pelo programa através da forma de introdução de Eoed, onde é possível especificar, para cada solo, a curva edométrica respetiva (diagrama σef/ε).
No entanto, a partir da experiência prática sugere-se (para argilas, por exemplo) diferentes ordens de grandeza entre o valor de Eoed derivado a partir do módulo de deformação Edef e que é obtido a partir da medição in situ da curva de carga.
A relação entre Edef e Eoed é dada por:
![]()
![]()
| onde: | ν | – | coeficiente de Poisson |
| Edef | – | módulo de deformação |
Intervalo de valores aproximado para módulos edométricos de deformação Eoed para cada solo e intervalos de tensão típicos (prof. I. Vanicek: Soil mechanics):
| Solo | Módulo edométrico Eoed [MPa] |
| cascalhos | 60 – 600 |
| areias mediamente densas a areias densas | 7 – 130 |
| coesivo | 2 – 30 |
Bibliografia:
Vanicek, I.: Geomechanika 10: mechanika zemin. 3th edition, Prague, CTU, 2000, 229 s., ISBN 80-01-01437-1.
Constante de Compressão
Ao desenhar a curva de tensão vertical efetiva em função deformação vertical na escala semi-logarítmica, obtém-se uma dependência linear.
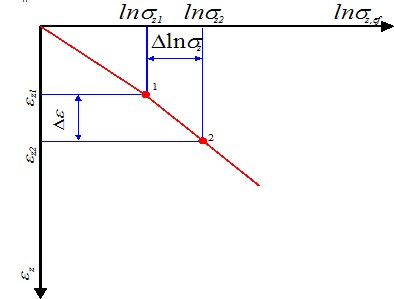 Determinação da constante de compressão C
Determinação da constante de compressão C
A inclinação desta curva é um dos parâmetros do solo, particularmente no caso de deformações unidimensionais, e é referida como constante de compressão C:
![]()
| onde: | σ1ef | – | tensão efetiva inicial do solo no edómetro |
| σ2ef | – | tensão efetiva final do solo no edómetro |
Limites da constante de compressão C (J.Šimek: Mechanika zemin)
| Solo | Constante de compressão C [-] |
| Silte loesse | 15 – 45 |
| Argila | 30 – 120 |
| Silte | 60 – 150 |
| areias mediamente densas a areias densas | 150 – 200 |
| Areia com cascalho | > 250 |
Constante de Compressão 10
Na prática da engenharia, o logaritmo de base natural é, por vezes, substituído pelo logaritmo de base 10, para definir a tensão σef. Neste caso, é comum usar o índice 10 na constante de compressão: C10. Esta é dada por:
![]()
É possível derivar a relação entre a constante de compressão C e C10:
![]()
Arnold Verruijt (Soil Mechanics) propõe os seguintes valores para a constante de compressão:
| Solo | C | C10 |
| Areia | 50 – 500 | 20 – 200 |
| Silte | 25 – 125 | 10 – 50 |
| Argila | 10 – 100 | 4 – 40 |
| Turfa | 2 – 25 | 1 – 10 |
Bibliografia:
Arnold Verruijt: Soil mechanics, Delft University of Technology, 2001, 2006, http://geo.verruijt.net/.
Índice de Vazios
O índice de vazios e descreve a porosidade de um solo e é dado por:
![]()
| onde: | Vp | – | volume de vazios |
| Vs | – | volume de sólidos |
Intervalos para o índice de vazios e (Braja M. DAS: Principles of Foundation Engineering)
| Solos | Índice de vazios e [-] |
| Areia mal graduada com baixa densidade | 0.8 |
| Areia densa bem graduada | 0.45 |
| Areia solta com baixa densidade e com partículas angulares | 0.65 |
| Areia densa com densidade elevada e com partículas angulares | 0.4 |
| Argila rígida | 0.6 |
| Argila mole | 0.9 – 1.4 |
| Loesse | 0.9 |
| Argila orgânica mole | 2.5 – 3.2 |
| Tilito glaciar | 0.3 |
Índice de Recompressão
O índice de recompressão Cr é determinado a partir do gráfico que representa a variação do índice de vazios e em função da tensão efetiva σef, numa escala logarítmica, para uma sequência de carregamento – relaxamento:
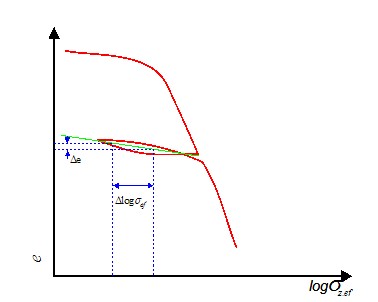 Determinação do índice de recompressão Cr
Determinação do índice de recompressão Cr
![]()
| onde: | Δe | – | variação do índice de vazios para a curva carregamento-relaxamento |
| Δlogσef | – | variação da tensão efetiva para a curva carregamento-relaxamento |
Se não estiverem disponíveis resultados de ensaios de laboratório ou in situ, o índice de recompressão Cr pode ser estimado a partir de:
![]()
| onde: | Cc | – | constante de compressão |
Características de Janbu
Valores do módulo de Janbu m e do expoente de tensão j (de acordo com o Canadian Foundation Engineering Manual 1992)
| Solo | Módulo de Janbu m | Índice de tensão j |
| Tilite muito denso a denso, tilite glaciar | 1000 – 300 | 1 |
| Cascalho | 400 – 40 | 0.5 |
| Areia densa | 400 – 250 | 0.5 |
| Areia em condições médias | 250 – 150 | 0.5 |
| Areia solta | 150 – 100 | 0.5 |
| Silte denso | 200 – 80 | 0.5 |
| Silte em condições médias | 80 – 60 | 0.5 |
| Silte solto | 60 – 40 | 0.5 |
| Argila dura a muito rígida | 60 – 20 | 0 |
| Argila média a rígida | 20 – 10 | 0 |
| Silte argiloso mole | 10 – 5 | 0 |
| Argilas marinhas moles | 20 – 5 | 0 |
| Argilas orgânicas | 20 – 5 | 0 |
| Turfas | 5 – 1 | 0 |
Influência do Histórico do Carregamento
O histórico do carregamento tem uma influência substancial na distribuição da curva de deformação e, consequentemente, também nos valores das características da deformação. A figura seguinte mostra a curva de deformação (diagrama Δe = f(Δσef)) derivado a partir do ensaio de carregamento edométrico correspondente, por exemplo, a um solo arenoso natural denso.
 Histórico de carregamento a) Curva de deformação para solos argilosos a partir de ensaio edométrico b) Interpretação simplificada da curva de deformação
Histórico de carregamento a) Curva de deformação para solos argilosos a partir de ensaio edométrico b) Interpretação simplificada da curva de deformação
A amostra de solo foi gradualmente carregada até atingir o nível de tensão σbef, a relação tensão-deformação (σbef – ε) dentro da secção a-b é linear e é denotada como primária ou virgem (isto é, a compressão relativa é obtida). Ao exceder o nível de tensão σbef, a amostra foi descarregada elasticamente e o solo moveu-se na direção ascendente para a secção b-c da curva de deformação. Após novo carregamento, o solo moveu-se na direção descendente, desde a secção b-c, até atingir a tensão original σbef, antes de novo relaxamento. Ao realizar um carregamento superior a σbef, a curva de deformação aproxima-se, assintoticamente, da secção d-e, com a linha primária a ser acompanhada pela deformação inelástica da amostra do solo. Esta curva de tensão-deformação complexa é muitas vezes simplificada pela curva de deformação idealizada (fig. b). Esta curva caracteriza a sobreconsolidação dos solos, que estiveram sujeitos a tensões elevadas e a relaxamentos consecutivos. O rácio de sobreconsolidação (OCR) representa o rácio entre a tensão de pré-consolidação máxima que o solo alguma vez experimentou e a tensão vertical atual. Os solos sobreconsolidados apresentam a curva de deformação definida pelos pontos c-d-e. A alteração na inclinação ao longo desta linha (dada pelo ponto d) corresponde à tensão geostática vertical σo (solos normalmente consolidados) ou à pressão de pré-consolidação σc (solos sobreconsolidados). Este ponto influencia a deformação do solo, que é menor dentro da secção c-d, quando comparada com a secção d-e (onde para um nível de sobreconsolidação elevado a deformação do solo aumente). As características de deformação adicionais, como o módulo de deformação durante o relaxamento Ee, índice de expansão unidimensional Ce, índice de recompressão Cr, etc. são introduzidos para descrever o comportamento complexo do solo. Correntemente, o parâmetro do solo mais utilizado é o índice de recompressão Cr adequado para a computação do assentamento de solos sobreconsolidados.
Coeficiente m
O coeficiente de correção de sobrecargas devido à resistência estrutural m determina a resistência estrutural do solo.
Valores para o coeficiente de correção de sobrecargas m
| Tipo de solo fundamental | m |
Solos finos muito compressíveis de classe F1-F8 – com módulo de deformação Edef < 4 MPa – não sobreconsolidados – consistência mole a dura (todos os 3 requisitos devem ser verificados), enchimento feito de solo sedimentos secundários e terciários rochas de classe R1, R2 | 0.1 |
Solos finos de classe F1-F8, não pertencentes ao coeficiente m = 0.1 ou 0.4 ou 0.6 areias e cascalhos de classe S1, S2, G1, G2 abaixo do nível freático rochas de classe R3, R4 | 0.2 |
Areias e cascalhos de classe S1, S2, G1, G2 acima do nível freático areias e cascalhos com argila, silte ou mistura de solos fina solos de classe S3, S4, S5, G3, G4, G5 rochas de classe R5, R6 | 0.3 |
| eluvião de rochas ígneas e metamórficas | 0.4 |
Índice de Compressão Modificado
A análise com a aplicação do modelo de solo mole assenta no modelo elasto-plástico desenvolvido na Universidade de Cambridge. Aqui, a deformação vertical do solo ε assume uma dependência linear em relação à variação logarítmica da tensão efetiva de um solo. A aplicação deste modelo implica uma introdução ao índice de compressão modificada λ, usualmente obtido a partir de ensaios triaxiais.
Se o índice de compressão modificado λ não estiver disponível a partir de ensaios laboratoriais, este pode ser estimado a partir do índice de compressão CC:
![]()
| onde: | CC | – | índice de compressão |
| e | – | índice de vazios médio (se este valor não for conhecido, pode ser substituído pelo valor do índice de vazios inicial eo) |
Índice de Compressão Secundária
O índice de compressão secundária é proporcional à escala de tempo logarítmica e à inclinação da consolidação primária (é fortemente dependente na tensão efetiva final do solo):
![]()
| onde: | Cα | – | índice de compressão secundária |
| α | – | deformação da camada de solo | |
| t1 | – | tempo inicial do período de monitorização (medido desde o início da consolidação) | |
| t2 | – | tempo final do período de monitorização |
A determinação do valor do índice de compressão secundária Cα implica a realização de ensaios laboratoriais (ex.: consolidação unidimensional em edómetro) ou in situ:
 Determinação do índice de compressão secundária Cα
Determinação do índice de compressão secundária Cα
Intervalos de valores para o índice de compressão secundária Cα
| areia | 0.00003 – 0.00006 |
| silte loesse | 0.0004 |
| argila | 0.01 |
O rácio entre o índice de compressão secundária Cα e o índice de compressão Cc é aproximadamente constante para a maioria das argilas normalmente consolidadas, para carregamentos típicos na prática da engenharia. O valor médio é 0.05.
A figura mostra a variação da mistura natural de solos em função do índice de compressão secundária Cα, segundo Mesri:
 Variação da mistura natural de solos em função do índice de compressão secundária Cα
Variação da mistura natural de solos em função do índice de compressão secundária Cα
| 1 | Argila de Whangamarino |
| 2 | Argila da Cidade do México |
| 3 | Silte orgânico calcário |
| 4 | Argila de Leda |
| 5 | Argila plástica na Noruega |
| 6 | Turfa amorfa e fibrosa |
| 7 | Muskeg do Canadá |
| 8 | Depósitos marinhos orgânicos |
| 9 | Argila azul de Boston |
| 10 | Argila azul de Chicago |
| 11 | Argila siltosa orgânica |
Índice de Sobreconsolidação da Compressão Secundária
O índice de sobreconsolidação da compressão secundária é obtido através de ensaios laboratoriais (ex.: consolidação unidimensional) e é proporcional à escala temporal logarítmica e à inclinação da linha de consolidação virgem, se a pressão de pré-consolidação não for excedida:
![]()
| onde: | Cαr | – | índice de sobreconsolidação da compressão secundária |
| ε | – | deformação da camada do solo | |
| t1 | – | tempo inicial do período de monitorização (medido desde o início da consolidação) | |
| t2 | – | tempo final do período de monitorização |
Perda de Solo
A análise realizada no programa “Perda de Solo” pode ser dividida em dois grupos:
![]() Análise da forma da depressão acima das escavações
Análise da forma da depressão acima das escavações
![]() Análise da rotura de edifícios
Análise da rotura de edifícios
A análise da rotura de edifícios baseia-se na forma da depressão.
Análise da Depressão
A análise da depressão consiste num conjunto de passos:
![]() Determinação do assentamento máximo e dimensões da depressão para cada escavação
Determinação do assentamento máximo e dimensões da depressão para cada escavação
![]() Análise da forma da depressão
Análise da forma da depressão
![]() Cálculo da forma e dimensões da depressão para uma certa profundidade abaixo da superfície do terreno
Cálculo da forma e dimensões da depressão para uma certa profundidade abaixo da superfície do terreno
![]() Determinação da forma global da depressão para mais escavações
Determinação da forma global da depressão para mais escavações
![]() Processamento de outras variáveis (deformação horizontal, inclinação)
Processamento de outras variáveis (deformação horizontal, inclinação)
A análise do assentamento máximo e das dimensões da depressão podem ser realizadas através da teoria da perda de volume ou de teorias clássicas (Peck, Fazekas, Limanov).
Perda de Volume
O método da perda de volume é um método semi-empírico, com bases teóricas. O método introduz, de forma indireta, os parâmetros básicos da escavação na análise (estes incluem parâmetros mecânicos do meio, efeitos da tecnologia da escavação, revestimento da escavação, etc.), através de dois parâmetros compreensivos (coeficiente k para a determinação do ponto de inflexão e uma percentagem do volume perdido VL). Estes parâmetros definem a forma da depressão e são determinados empiricamente, com base em anos de experiência.
 Assentamento expresso em termos de volume
Assentamento expresso em termos de volume
O assentamento máximo Smax e a localização do ponto de inflexão Linf são obtidos através das seguintes expressões:
![]()
![]()
| onde: | A | – | área de escavação |
| Z | – | profundidade do ponto central da escavação | |
| k | – | coeficiente para calcular o ponto de inflexão (constante material) | |
| VL | – | percentagem do volume perdido |
A deformação do teto ua é dada por:
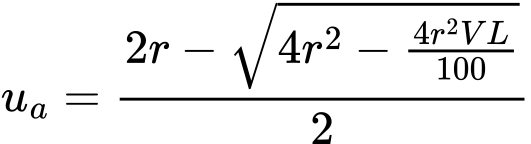
| onde: | r | – | raio da escavação |
| VL | – | percentagem de volume perdido |
Bibliografia:
http://www.groundloss.com/
Valores Recomendados para os Parâmetros da Análise da Perda de Volume
Dados necessários para a determinação da depressão através do método da perda de volume:
Coeficiente para calcular o ponto de inflexão k
| Solo ou rocha | k |
| solo não coesivo | 0,3 |
| argila normalmente consolidada | 0,5 |
| argila sobreconsolidada | 0,6 – 0,7 |
| ardósia de argila | 0,6 – 0,8 |
| quartzito | 0,8 – 0,9 |
Percentagem da perde de volume VL
| Tecnologia | VL |
| TBM | 0,5 – 1 |
| método de escavação sequencial | 0,8 – 1,5 |
Foram derivadas várias relações para determinar o valor da perda de volume VL, com base no rácio de estabilidade N, definido por Broms e Bennermarkem:
![]()
| onde: | σv | – | tensão global ao longo do eixo da escavação |
| σt | – | resistência do revestimento da escavação (se o revestimento estiver instalado) | |
| Su | – | rigidez da argila não drenada |
Para N < 2, o solo/rocha na vizinhança da escavação é assumido como elástico e estável. Para ![]() , começam a desenvolver-se zonas locais plásticas na vizinhança da escavação. Para
, começam a desenvolver-se zonas locais plásticas na vizinhança da escavação. Para ![]() , desenvolve-se uma zona plástica de grande dimensão à volta da escavação e para N = 6, dá-se a perda de estabilidade da superfície do túnel. A figura mostra a perda de volume VL em função do rácio de estabilidade.
, desenvolve-se uma zona plástica de grande dimensão à volta da escavação e para N = 6, dá-se a perda de estabilidade da superfície do túnel. A figura mostra a perda de volume VL em função do rácio de estabilidade.
Bibliografia:
Broms, B.B., Bennemark, H., 1967. Stability of clay at vertical openings. ASCE, Journal of Soil Mechanics and Foundation Engineering Division, SMI 93, 71-94.
Teoria Clássica
A análise de convergência de uma escavação e o cálculo do assentamento máximo de um corpo homogéneo são iguais para todas as teorias clássicas. A análise da depressão difere consoante a teoria assumida (Peck, Fazekas, Limanov).
Ao calcular o assentamento, o programa começa por determinar a carga radial de uma escavação circular:
![]()
| onde: | σz | – | tensão geostática no centro da escavação |
| Kr | – | coeficiente do empuxo em repouso do solo coesivo |
As deformações do teto ua e da base ub da escavação são dadas por:
![]()
![]()
| onde: | Z | – | profundidade do ponto central da escavação |
| r | – | raio de escavação | |
| E | – | módulo de elasticidade do solo/rocha na vizinhança da escavação | |
| ν | – | coeficiente de Poisson do solo/rocha na vizinhança da escavação |
O assentamento máximo do terreno e o comprimento da depressão são determinados através de:
![]()
![]()
| onde: | Z | – | profundidade do ponto central da escavação |
| r | – | raio de escavação | |
| E | – | módulo de elasticidade do solo/rocha na vizinhança da escavação | |
| ν | – | coeficiente de Poisson do solo/rocha na vizinhança da escavação |
Após determinar o deslocamento do teto do túnel, o assentamento máximo é dado pela expressão seguinte:
![]()
| onde: | Z | – | profundidade do ponto central da escavação |
| r | – | raio de escavação | |
| ua | – | deslocamento do teto do túnel | |
| ν | – | coeficiente de Poisson do solo/rocha na vizinhança da escavação |
Análise para Subsolo em Camadas
Ao determinar o assentamento de um subsolo por camadas, o programa começa por calcular o assentamento na interface entre a primeira camada acima da escavação e as outras camadas acima Sint e determina o comprimento da depressão ao longo das interfaces das camadas. Neste caso, a metodologia é a mesma que a utilizada para solos homogéneos.
Seguidamente (conforme mostra a Figura), o programa determina o comprimento da depressão L na superfície do terreno.
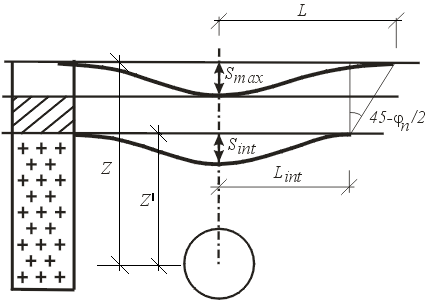 Análise do assentamento em subsolo por camadas
Análise do assentamento em subsolo por camadas
A próxima computação difere consoante a teoria de análise selecionada:
Método de acordo com Limanov
Limanov descreve o deslocamento horizontal acima da escavação com base na área perdida F:
![]()
| onde: | L | – | comprimento da depressão |
| F | – | perda de volume do solo por metro de desenvolvimento, determinado por: |
![]()
| onde: | Lint | – | comprimento da depressão ao longo das interfaces acima da escavação |
| Sint | – | assentamento de cada interface |
Método de acordo com Fazekas
Fazekas descreve o deslocamento horizontal acima da escavação através da expressão seguinte:
![]()
| onde: | L | – | comprimento da depressão |
| Lint | – | comprimento da depressão ao longo das interfaces acima da escavação | |
| Sint | – | assentamento de cada interface |
Método de acordo com Peck
Peck descreve o deslocamento horizontal acima da escavação através da expressão seguinte:
![]()
| onde: | Lint | – | comprimento da depressão ao longo das interfaces acima da escavação |
| Sint | – | assentamento de cada interface | |
| Linf | – | distância do ponto de inflexão da depressão a partir do eixo da escavação na superfície do terreno |
Bibliografia:
Széchy, Károly, The art of tunelling, Budapest : Akadémiai Kiadó, 1966.
Forma da Depressão
O programa oferece duas formas particulares para a depressão – de acordo com Gauss ou Aversin.
Curva segundo Gauss
Vários estudos realizados nos EUA e Reino Unido provam que pode ser obtida uma boa aproximação da forma transversal da depressão através da função de Gauss. Esta hipótese permite determinar o deslocamento horizontal, para a distância x, medida a partir do eixo de simetria vertical:
![]()
| onde: | Si | – | assentamento no ponto de coordenada xi |
| Smax | – | assentamento máximo do terreno | |
| Linf | – | distância do ponto de inflexão |
Curva segundo Aversin
Aversin determinou, com base em observações e registos de estruturas subterrâneas na Rússia, a seguinte expressão para a forma da depressão:
![]()
| onde: | Si | – | assentamento no ponto de coordenada xi |
| Smax | – | assentamento máximo do terreno | |
| L | – | comprimento da depressão |
Bibliografia:
Széchy, Károly, The art of tunelling, Budapest : Akadémiai Kiadó, 1966.
Coeficiente para o Cálculo do Ponto de Inflexão
Quando os métodos clássicos são utilizados, o coeficiente introduzido kinf permite determinar a localização do ponto de inflexão, com base em Linf = L/kinf. Neste caso, o coeficiente kinf representa um parâmetro extremamente importante que influencia bastante a forma e a inclinação da depressão. O seu valor depende do solo ou rocha acima da escavação – a bibliografia disponibiliza valores para kinf dentro do intervalo 2,1 – 4,0.
Os valores seguintes são recomendados, com base numa série de cálculos MEF:
| solo de cascalho G1-G3 | kinf = 3,5 | |
| solo de areia e cascalho S1-S5,G4,G5, rochas R5-R6 | kinf = 3,0 | |
| solo de graduação fina F1-F4 | kinf = 2,5 | |
| solo de graduação fina F5-F8 | kinf = 2,1 |
O coeficiente para o cálculo do ponto de inflexão é introduzido na janela “Configurações”.
Depressão com Várias Escavações
O princípio da sobreposição é utilizado ao calcular o assentamento provocado por escavações estruturadas ou múltiplas. Com base nos parâmetros introduzidos, o programa começa por determinar a depressão e os deslocamentos horizontais para cada escavação. A depressão global é determinada consequentemente.
Outras variáveis, distensão horizontal e inclinação da depressão, são processadas a partir da depressão global.
Análise em Profundidade da Depressão
Uma interpolação linear entre o valor máximo do assentamento Smax na superfície do terreno e o deslocamento no tero da escavação ua é utilizada para calcular o assentamento máximo S à profundidade h abaixo da superfície do terreno, num solo homogéneo.
 Análise da depressão para uma profundidade
Análise da depressão para uma profundidade
A largura da depressão na zona da sobrecarga l é dada por:
![]()
| onde: | L | – | comprimento da depressão na superfície do terreno |
| r | – | raio da escavação | |
| Z | – | profundidade do ponto central | |
| z | – | profundidade da análise |
Os valores l e S são utilizados para determinar a forma da depressão sobrecarregada, acima da escavação.
Cálculo de Outras Variáveis
Um assentamento vertical é acompanhado pela evolução de deslocamentos horizontais que podem causar danos em edifícios nas proximidades. O deslocamento horizontal pode ser derivado a partir do assentamento vertical, se os vetores de assentamento resultantes tiverem a direção do centro da escavação. Neste caso, o deslocamento horizontal do solo é dado através da seguinte equação:
![]()
| onde: | x | – | distância do ponto x em relação ao eixo da escavação |
| s(x) | – | assentamento no ponto x | |
| Z | – | profundidade do ponto central da escavação | |
| r | – | raio da escavação |
Os deslocamentos horizontais são determinados de forma diferencial ao longo do eixo x e podem ser expressos na direção transversa através da seguinte equação:
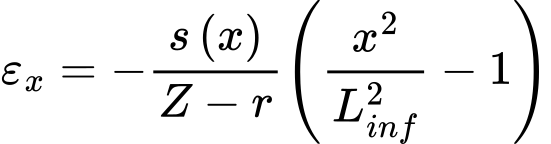
| onde: | x | – | distância do ponto x em relação ao eixo da escavação |
| s(x) | – | assentamento no ponto x | |
| Z | – | profundidade do ponto central da escavação | |
| Linf | – | distância do ponto de inflexão | |
| r | – | raio da escavação |
Análise de Rotura em Edifícios
O programa começa por determinar a forma e dimensões da depressão e, seguidamente, realiza a análise da sua influência em edifícios.
O programa permite quatro tipos de análise:
![]() Determinação de fendas
Determinação de fendas
![]() Determinação da escala de danos
Determinação da escala de danos
![]() Determinação da deflexão relativa de edifícios (côncavo, convexo)
Determinação da deflexão relativa de edifícios (côncavo, convexo)
![]() Análise da secção introduzida de um edifício
Análise da secção introduzida de um edifício
Fendas
Uma das causas responsáveis pelos danos nos edifícios são as distensões horizontais de tração. O programa evidencia as partes do edifício consoante a nível de danos, através de uma escala de cores. O valor máximo para a deformação à tração é exibido no relatório de texto.
O programa possibilita a análise danos em zonas pré-definidas para edifícios de alvenaria. Estes valores podem ser modificados na janela “Configurações da etapa”. A partir da experiência obtida com a construção de vários túneis escavados sob áreas edificadas, foi possível elaborar uma relação entre a forma da depressão e o dano provocado nos edifícios, com precisão tal que é possível estimar uma gama de compensações para os danos possíveis, causados pela escavação, com um nível de confiança suficiente para preparar documentos contratuais e para os empreiteiros prepararem propostas para a escavação de túneis.
A tabela seguinte apresenta valores recomendados para edifícios de alvenaria, com um a seis pisos.
Distensões horizontais (por milha)
| D.h. proporcional (por milha) | Danos | Descrição |
| 0,2 – 0,5 | Micro-fendas | Micro-fendas |
| 0,5 – 0,75 | Danos pequenos – superficiais | Fendas no reboco |
| 0,75 – 1,0 | Danos pequenos | Pequenas fendas nas paredes |
| 1,0 – 1,8 | Danos médios, funcional | Fendas nas paredes, problemas com janelas e portas |
| 1,8 – | Danos elevados | Fendas grandes em paredes e vigas de suporte |
Escala de Danos
Uma das causas que origina danos em edifícios é a inclinação da depressão. O programa evidencia as partes do edifício consoante a nível de danos, através de uma escala de cores. O valor máximo para a deformação à tração é exibido no relatório de texto.
O programa possibilita a análise danos em zonas pré-definidas para edifícios de alvenaria. Estes valores podem ser modificados na janela “Configurações da etapa”. A partir da experiência obtida com a construção de vários túneis escavados sob áreas edificadas, foi possível elaborar uma relação entre a forma da depressão e o dano provocado nos edifícios, com precisão tal que é possível estimar uma gama de compensações para os danos possíveis, causados pela escavação, com um nível de confiança suficiente para preparar documentos contratuais e para os empreiteiros prepararem propostas para a escavação de túneis.
A tabela seguinte apresenta valores recomendados para edifícios de alvenaria, com um a seis pisos.
Escala
| Escala | Danos | Descrição |
| 1:1200 – 800 | Micro-fendas | Micro-fendas |
| 1:800 – 500 | Danos pequenos – superficiais | Fendas no reboco |
| 1:500 – 300 | Danos pequenos | Pequenas fendas nas paredes |
| 1:300 – 150 | Danos médios, funcional | Fendas nas paredes, problemas com janelas e portas |
| 1:150 – 0 | Danos elevados | Fendas grandes em paredes e vigas de suporte |
Deflexão Relativa
A definição do termo deflexão relativa é evidente a partir da figura. O programa procura as regiões dos edifícios com a deflexão relativa máxima, na direção ascendente e descendente. A partir do ponto de vista de danos do edifício, a deflexão relativa mais crítica é na direção ascendente, o que provoca uma “abertura de tração” no edifício.
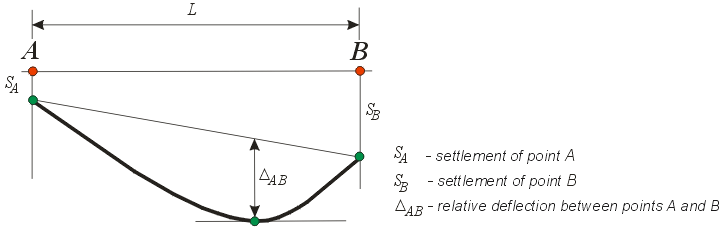 Deflexão relativa
Deflexão relativa
A verificação da deflexão relativa máxima é da responsabilidade do usuário – a tabela seguinte apresenta os valores últimos, recomendados na bibliografia.
| Tipo de estrutura | Tipo de danos | Deflexão relativa última Δ/l | |||
| Burland e Wroth | Meyerhof | Polshin e Tokar | ÈSN 73 1001 | ||
| Paredes de suporte não armadas | Fendas em paredes | Para L/H = 1 – 0.0004 Para L/H = 5 – 0.0008 | 0.0004 | 0.0004 | 0.0015 |
| Fendas em estruturas de suporte | Para L/H = 1 – 0.0002 Para L/H = 5 – 0.0004 | – | – | – | |
Rotura da Secção de um Edifício
Para uma dada secção, o programa determina as seguintes variáveis:
![]() fenda máxima
fenda máxima
![]() escala máxima
escala máxima
![]() deflexão relativa máxima
deflexão relativa máxima
![]() gradiente relativo entre os pontos introduzidos de um edifício
gradiente relativo entre os pontos introduzidos de um edifício
A avaliação da secção analisada é da responsabilidade do usuário – a tabela seguinte apresenta os valores últimos, recomendados na bibliografia.
| Tipo de estrutura | Tipo de danos | Gradiente relativo último | ||||
| Skempton | Meyerhof | Polshin e Tokar | Bjerrum | CSN 73 1001 | ||
| Pórticos e paredes de suporte reforçadas | Estruturais | 1/150 | 1/250 | 1/200 | 1/150 | |
| Fendas em paredes | 1/300 | 1/500 | 1/500 | 1/500 | 1/500 | |
| Tipo de estrutura | Tipo de danos | Deflexão relativa última Δ/l | |||
| Burland e Wroth | Meyerhof | Polshin e Tokar | CSN 73 1001 | ||
| Paredes de suporte não armadas | Fendas em paredes | Para L/H = 1 – 0.0004 Para L/H = 5 – 0.0008 | 0.0004 | 0.0004 | 0.0015 |
| Fendas em estruturas de suporte | Para L/H = 1 – 0.0002 Para L/H = 5 – 0.0004 | – | – | – | |
Estruturas de Concreto
As estruturas de concreto pode ser analisadas de acordo com as seguintes Normas:
![]() EN 1992-1-1 (EC 2) ou EN 1992-2
EN 1992-1-1 (EC 2) ou EN 1992-2
![]() CSN 73 1201R
CSN 73 1201R
![]() CSN 73 6206 (apenas para Encontro de Pontes)
CSN 73 6206 (apenas para Encontro de Pontes)
![]() PN-B-03264:2002
PN-B-03264:2002
![]() BS 8110:1997
BS 8110:1997
![]() IS 456ACI 318-11
IS 456ACI 318-11
![]() AS 3600-2001
AS 3600-2001
![]() SNiP 52-101-200
SNiP 52-101-200
![]() GB 50010-2010
GB 50010-2010
![]() NZS 3101-2006
NZS 3101-2006
![]() CSA A23.3-14
CSA A23.3-14
![]() NBR 6118-2014
NBR 6118-2014
EN 1992-1-1 (EC2) ou EN 1992-2
Esta ajuda contém os seguintes métodos:
![]() Materiais, coeficientes, notações
Materiais, coeficientes, notações
![]() Valores standard de coeficientes
Valores standard de coeficientes
![]() Verificação de secções transversais retangulares em concreto simples
Verificação de secções transversais retangulares em concreto simples
![]() Verificação de secções transversais retangulares em concreto armado
Verificação de secções transversais retangulares em concreto armado
![]() Verificação de secções transversais circulares em concreto armado
Verificação de secções transversais circulares em concreto armado
![]() Verificação de sapatas para o cisalhamento
Verificação de sapatas para o cisalhamento
![]() Dimensionamento de armaduras longitudinais para lajes
Dimensionamento de armaduras longitudinais para lajes
![]() Dimensionamento de armaduras de cisalhamento para lajes
Dimensionamento de armaduras de cisalhamento para lajes
![]() Verificação da dimensão de fendas
Verificação da dimensão de fendas
Materiais, Coeficientes, Notações
É utilizada a seguinte notação para os parâmetros materiais:
| fck | – | valor característico da resistência cilíndrica do concreto à compressão |
| fcd | – | resistência de dimensionamento do concreto à compressão |
| fcm | – | valor médio da resistência do concreto à compressão |
| fctm | valor médio da resistência do concreto à tração | |
| fctk0,05 | – | valor característico reduzido da resistência do concreto à tração |
| fctd | – | resistência de dimensionamento do concreto à tração |
| fyk | – | resistência característica do aço |
| fyd | – | resistência de dimensionamento do aço à tração |
A resistência característica do concreto à compressão é o parâmetro básico a introduzir dado pela classe do concreto – serve para derivar os restantes coeficientes (Tbl. 3.1).
| for: fck ≤ 50 Mpa | |
| for: fck > 50 Mpa | |
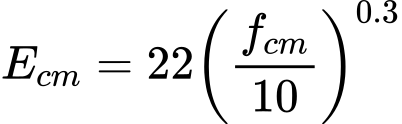 | |
Os valores standard dos coeficientes αcc, γc, αct, γs estão integrados no programa – estes valores também podem ser introduzidos pelo usuário, consoante o Anexo Nacional selecionado.
podem
Notação mais comum para os parâmetros geométricos:
| b | – | largura da secção transversal |
| h | – | altura da secção transversal |
| d | – | altura efetiva da secção transversal |
| z | – | braço (braço das forças internas) |
Valores Standard de Coeficientes
Os programas contém um conjunto de coeficientes com valores padrão, que podem ser ajustados de acordo com os Anexos Nacionais. A tabela contém a descrição de cada coeficiente, o valor e o artigo correspondente da Norma que o apresenta. Em alguns casos, a equação que permite calcular a coeficiente contém uma variável que não apresenta nenhuma notação específica nos programas – nestes casos, esta variável aparece na expressão como X.
| Coeficiente | Valor | Notações | Artigo |
| γc | 1,5 | 2.4.2.4 | |
| γs | 1,15 | 2.4.2.4 | |
| αcc | 1 | 3.1.6 | |
| αct | 1 | 3.1.6 | |
| αcc,pl | 0,8 | 12.3.1 | |
| αct,pl | 0,8 | 12.3.1 | |
| k | 1,5 | 12.6.3 | |
| ρmin | 0,0013 | 9.2.1.1 | |
| X | 0,26 | 9.2.1.1 | |
| ρmax | 0,04 | 9.2.1.1 | |
| ρmin | 0,002 | 9.5.2 | |
| X | 0,1 | 9.5.2 | |
| ρmax | 0,04 | 9.5.2 | |
| X | 0,18 | 6.2.2 | |
| νmin | – | 6.2.2 | |
| X | 0,5 | 6.2.2 | |
| ν | – | 6.2.2 | |
| cot θmin | 1 | 6.2.3 | |
| cot θmax | 2,5 | 6.2.3 |
Anexo Nacional da República Checa (CSN EN 1992-1-1 – 2010)
| Coeficiente | Valor | Notações | Artigo |
| αct,pl | 0,7 | 12.3.1 |
os outros valores são standard
Anexo Nacional da Eslováquia (STN EN 1992-1-1 – 2008)
todos os valores são standard
Anexo Nacional da Polónia (PN EN 1992-1-1 – 2008)
| Coeficiente | Valor | Notações | Artigo |
| γc | 1,4 | 2.4.2.4 | |
| cot θmax | 2,0 | 6.2.3 |
os outros valores são standard
Anexo Nacional da Noruega (NS EN 1992-1-1 – 2004)
| Coeficiente | Valor | Notações | Artigo |
| αcc | 0,85 | 3.1.6 | |
| αct | 0,85 | 3.1.6 |
os outros valores são standard
Anexo Nacional da Roménia (BDS EN 1992-1-1 – 2005)
todos os valores são standard
Anexo Nacional de Itália (UNI EN 1992-1-1 – 2005)
| Coeficiente | Valor | Notações | Artigo |
| αcc | 0,85 | 3.1.6 | |
| ν | 0,5 for ≤C70/85 | 6.2.2 |
os outros valores são standard
National Annex United Kingdom (BS EN 1992-1-1 – 2004)
| Coeficiente | Valor | Notações | Artigo |
| αcc | 0,85 | 3.1.6 | |
| αcc,pl | 0,6 | 12.3.1 | |
| αct,pl | 0,6 | 12.3.1 |
os outros valores são standard
EN 1992-2 – 2007
| Coeficiente | Valor | Notações | Artigo |
| αcc | 0,85 | 3.1.6 |
os outros valores são standard
Verificação de Secções Transversais Retangulares em Concreto Simples
A secção transversal é retangular, carregada pelo momento fletor MEd, pela força normal NEd (aplicada no centroide da secção transversal) e pela força de cisalhamento VEd. A resistência ao cisalhamento é dada por (Art. 12.6.3):
![]()
onde: Acc – área do concreto à compressão
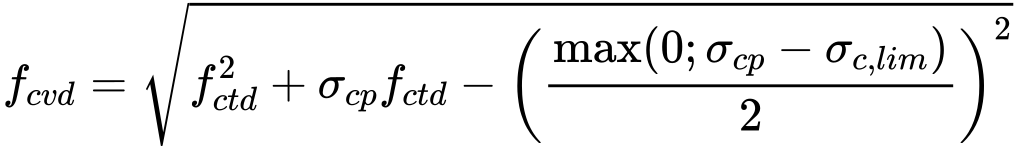
![]()
![]()
O valor standard do coeficiente k está inserido nos programas (Art. 12.6.3) – este valor também pode ser ajustado no programa, com base no Anexo Nacional selecionado.
A resistência da secção transversal em concreto está sujeita a uma combinação do momento fletor e da forçar normal, que é dada pelas expressões seguintes (Art. 12.6.1), com base na excentricidade da força normal e:
Como o máximo entre:
![]()
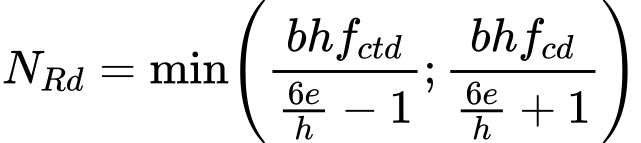
A fórmula permite definir a resistência a partir do diagrama tensão-deformação da secção transversal sem fendilhação.
![]()
![]()
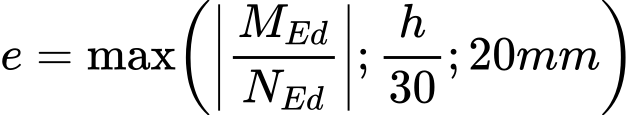
Os valores mínimos para a excentricidade estão presentes no artigo 6.1(3).
![]()
![]()
Os valores standard dos coeficientes αcc,pl, αct,pl, γc estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
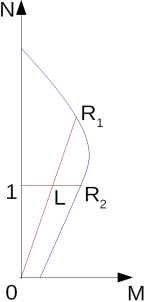 Diagrama de interação N-M
Diagrama de interação N-M
O rácio de utilização de concreto da secção transversal está sujeito à combinação do momento fletor com a força normal e é determinado como |0L| / |0R1| ou |1L| / |1R2|. Onde L é a carga, R1 é a resistência para uma certa excentricidade e R2 é a resistência para uma certa força normal.
Verificação de Secções Transversais Retangulares em Concreto Armado
A secção transversal é retangular, armada unilateralmente e carregada pela momento fletor e força normal de compressão. O programa verifica a secção de concreto armado através do método da deformação limite. A deformação máxima permitida para o concreto à compressão é 0,002 a 0,0035. Não é considerada armadura para a compressão. A excentricidade mínima é dada por (Art. 6.1(3)):
![]()
A quantidade de armadura computada é verificada de acordo com as expressões seguintes (Art. 9.2.1.1):
![]()
![]()
![]()
![]()
Os valores standard dos coeficientes ρmin, ρmax estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
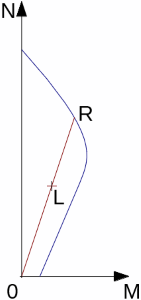 Diagrama de interação N-M
Diagrama de interação N-M
O rácio de utilização de concreto da secção transversal está sujeito à combinação do momento fletor com a força normal e é determinado como |0L| / |0R|. Onde L é a carga e R é a resistência para uma certa excentricidade.
Flexão sem força normal
A secção transversal é retangular, armada unilateralmente e carregada pelo momento fletor MEd.
O momento permitido para uma certa área de de armadura As é dado por (Art. 6.1, Art. 3.1.7(3)):
![]()
![]()
![]()
![]()
Os limites para a localização do eixo neutro são dados por (Art. 5.6.3(2)):
| xmax = 0,45d | para concreto C40/45 e inferior |
| xmax = 0,35d | para concreto C45/50 e superior |
Cisalhamento
Inicialmente, o programa computa a resistência ao cisalhamento última do concreto VRd,c (Art. 6.2.2(1)).
![]()
onde:
![]()
![]()
Se a resistência ao cisalhamento última do concreto for excedida, a resistência ao cisalhamento última VRd,max´ é assumida (Art. 6.2.3(3)):
![]()
Seguidamente, a área de armadura necessária é dada por (Art. 6.2.3(3)):
![]()
Os valores standard dos coeficientes ν, νmax, cot θmin, cot θmax estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
Verificação de Secções Transversais Circulares em Concreto Armado
O programa verifica uma estaca de concreto armado através do método da deformação limite. A deformação máxima permitida para o concreto à compressão é 0,002 – 0,0035. A resistência do concreto η*fcd é reduzida em dez por cento devido à forma da secção transversal (Art. 3.1.7).
A quantidade de armadura é verificada a partir da seguinte expressão:
![]()
![]() Estaca (Art. 9.8.5)
Estaca (Art. 9.8.5)
![]()
| Ac ≤ 0,5m2 | ρmin = 0,005 |
| 0,5m2 < Ac ≤ 1m2 | ρmin = 0,0025m2/Ac |
| Ac ≥ 1m2 | ρmin = 0,0025 |
| onde: | Ac | – | secção transversal da área da estaca |
![]()
![]() Pilar – verificação da compressão dominante (Art. 9.5.2)
Pilar – verificação da compressão dominante (Art. 9.5.2)
![]()
![]()
![]()
![]() Viga – verificação da flexão dominante (Art. 9.2.1.1)
Viga – verificação da flexão dominante (Art. 9.2.1.1)
![]()
![]()
![]()
| onde: | d | – | diâmetro da estaca |
| As | – | área armada da secção transversal |
Os valores standard dos coeficientes ρmin, ρmax estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
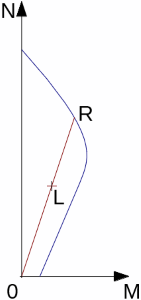 Diagrama de interação N-M
Diagrama de interação N-M
O rácio de utilização de concreto da secção transversal está sujeito à combinação do momento fletor com a força normal e é determinado como |0L| / |0R|. Onde L é a carga e R é a resistência para uma certa excentricidade.
Cisalhamento
Inicialmente, o programa computa a resistência ao cisalhamento última do concreto VRd,c (Art. 6.2.2(1)). As fórmulas estão presentes no Art. 6.2.2(1), onde a largura da secção (bw) é substituída por 0,88d e a profundidade efetiva (d) é substituída por 0,8d.
![]()
onde:
![]()
![]()
Se a resistência ao cisalhamento última do concreto for excedida, a resistência ao cisalhamento última VRd,max e a resistência da secção armada VRd,s são verificadas (Art. 6.2.3(3)).
![]()
![]()
Os valores standard dos coeficientes ν, νmin, cot θmin, cot θmax estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
Verificação de Secções Transversais Circulares em Concreto Armado
O programa verifica uma estaca de concreto armado através do método da deformação limite. A deformação máxima permitida para o concreto à compressão é 0,002 – 0,0035. A resistência do concreto η*fcd é reduzida em dez por cento devido à forma da secção transversal (Art. 3.1.7).
A quantidade de armadura é verificada a partir da seguinte expressão:
![]()
![]() Estaca (Art. 9.8.5)
Estaca (Art. 9.8.5)
![]()
| Ac ≤ 0,5m2 | ρmin = 0,005 |
| 0,5m2 < Ac ≤ 1m2 | ρmin = 0,0025m2/Ac |
| Ac ≥ 1m2 | ρmin = 0,0025 |
| onde: | Ac | – | secção transversal da área da estaca |
![]()
![]() Pilar – verificação da compressão dominante (Art. 9.5.2)
Pilar – verificação da compressão dominante (Art. 9.5.2)
![]()
![]()
![]()
![]() Viga – verificação da flexão dominante (Art. 9.2.1.1)
Viga – verificação da flexão dominante (Art. 9.2.1.1)
![]()
![]()
![]()
| onde: | d | – | diâmetro da estaca |
| As | – | área armada da secção transversal |
Os valores standard dos coeficientes ρmin, ρmax estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
 Diagrama de interação N-M
Diagrama de interação N-M
O rácio de utilização de concreto da secção transversal está sujeito à combinação do momento fletor com a força normal e é determinado como |0L| / |0R|. Onde L é a carga e R é a resistência para uma certa excentricidade.
Cisalhamento
Inicialmente, o programa computa a resistência ao cisalhamento última do concreto VRd,c (Art. 6.2.2(1)). As fórmulas estão presentes no Art. 6.2.2(1), onde a largura da secção (bw) é substituída por 0,88d e a profundidade efetiva (d) é substituída por 0,8d.
![]()
onde:
![]()
![]()
Se a resistência ao cisalhamento última do concreto for excedida, a resistência ao cisalhamento última VRd,max e a resistência da secção armada VRd,s são verificadas (Art. 6.2.3(3)).
![]()
![]()
Os valores standard dos coeficientes ν, νmin, cot θmin, cot θmax estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
Verificação de Sapatas para o Cisalhamento
As sapatas são carregadas pelos momentos MEx, MEy e pela força de cisalhamento VE, de acordo com:
![]()
| onde: | A | – | área da sapata |
| V | – | força vertical desenvolvida no pilar atribuída | |
| At | – | área hachurada da fig. |
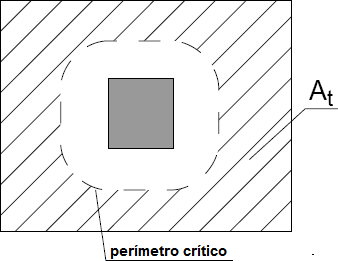 Dimensionamento da área de armadura para o cisalhamento At
Dimensionamento da área de armadura para o cisalhamento At
O programa simula secções de controlo à distância de 0,5d a 2d, no caso de sapatas sem armadura para cisalhamento. No caso de sapatas reforçadas, as distâncias são de 0,5d a 4d, onde d é a profundidade efetiva da sapata. A armadura para cisalhamento é considerada nas secções de controlo, que estão a uma distância inferior a 2d do pilar. As secções de controlo são consideradas em intervalos de 0,25d.
A tensão do carregamento VEd em cada secção de controlo é obtida através de 6.4.3 (3),
![]()
![]()
![]()
a resistência ao punçoamento da sapata sem armadura para o cisalhamento VRd,c é obtida através de 6.4.4 (2)
![]()
![]()
![]()
e, se necessário, a resistência ao punçoamento para sapatas armadas VRd,cs é obtida através de 6.4.5 (1).
![]()
![]()
A resistência à compressão no centro do pilar VRd,max é calculada de acordo com 6.4.5 (3). VRd,max depende das dimensões do pilar e da espessura da sapata.
![]()
Para vEd < vRd,c, não é necessária armadura para cisalhamento.
Para vEd > vRd,c e vEd < vRd,max, deve ser introduzida armadura para cisalhamento
Para vEd > vRd,max, a resistência para o cisalhamento não pode ser dimensionada. É necessário aumentar a altura da secção transversal.
A secção de controlo com o pior rácio de carregamento e resistência é considerada como a crítica e assinalada pelo programa.
Os valores standard dos coeficientes ν, νmin estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
Dimensionamento de Armaduras Longitudinais para Lajes
O dimensionamento de armaduras é realizado para cargas devido a momentos fletores MEd. O programa fornece a área necessária para armaduras de tração e compressão (se necessário). São consideradas as condições para as quantidades de armadura máximas e mínimas para a secção transversal em análise. O programa começa por determinar a localização do eixo neutro conforme o descrito em (Art. 3.1.7, Art. 6.1):
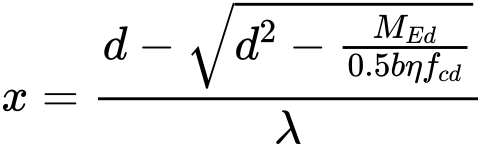
Se a localização do eixo neutro for inferior ao permitido (x < xmax), o programa determina a área da armadura de tração Ast a partir da expressão:
![]()
Se a localização do eixo neutro for superior ao permitido (x > xmax), o programa determina a área das armaduras de compressão Asc e de tração Ast a partir das expressões:
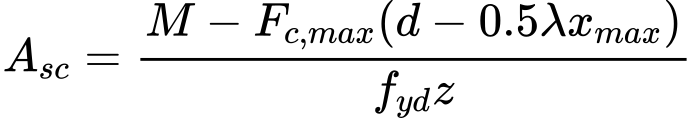
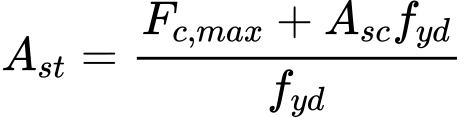
![]()
Os limites para a localização do eixo neutro são dados por (Art. 5.6.3(2)):
| xmax = 0,45d | para concreto C40/45 e inferior |
| xmax = 0,35d | para concreto C45/50 e superior |
A quantidade de armadura computada é verificada através das expressões seguintes (Art. 9.3.1.1):
![]()
![]()
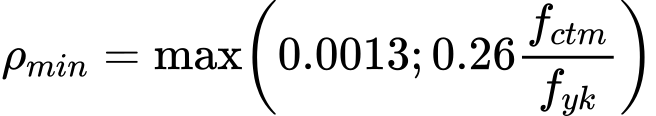
![]()
Os valores standard dos coeficientes ρmin, ρmax estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
Se a quantidade máxima de armadura total ρmax for excedida, o programa informa o usuário que a armadura longitudinal não pode ser dimensionada para a secção transversal em análise.
Dimensionamento de Armaduras de Cisalhamento para Lajes
O programa permite determinar a quantidade necessária de armadura para o cisalhamento a partir de estribos e tirantes curvos.
O programa começa por computar a resistência ao cisalhamento última de uma dada secção – a força de cisalhamento transmitida pelo concreto VRd, c (Art. 6.2.2(1)) e a força de cisalhamento máxima permitida VRd, max (Art. 6.2.3(3)).
![]()
onde:
![]()
![]()
![]()
Para estribos, a área de armadura necessária é dada por (Art. 6.2.3(3)):
![]()
Para tirantes curvos, a área de armadura necessária é dada por (Art. 6.2.3(4)):
![]()
Os valores standard dos coeficientes ν, νmin estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
Verificação da Dimensão de Fendas
A largura das fendas é avaliada de acordo com o capítulo 7.3.4 da Norma.
A tensão máxima no concreto é calculada para a secção ideal. Se a tensão for inferior à resistência do concreto fctm, não ocorre fendilhação.
Caso contrário, a largura das fendas é determinada de acordo com:
![]()
onde
![]()
onde σs é a tensão na armadura para tração, determinada para a secção ideal fendilhada
![]()
![]()
![]()
![]()
Se a distância entre as barras da armadura for igual ou inferior a 5(c+ϕ/2):
![]()
| onde: | k1 | = | 0,8 |
| k2 | = | 0,5 | |
| k3 | = | 3,4 | |
| k4 | = | 0,425 | |
| c | – | cobrimento | |
| ϕ | – | diâmetro da barra de aço |
Se a distância entre as barras da armadura for superior a 5(c+ϕ/2):
![]()
CSN 73 1201 R
This help contains the following computationals methods:
![]() Materials, coefficients, notation
Materials, coefficients, notation
![]() Verification of rectangular cross-section made from plain concrete
Verification of rectangular cross-section made from plain concrete
![]() Verification of rectangular RC cross-section
Verification of rectangular RC cross-section
![]() Verification of circular RC cross-section
Verification of circular RC cross-section
![]() Verification of spread footing for punching shear
Verification of spread footing for punching shear
![]() Design of longitudinal reinforcement for slabs
Design of longitudinal reinforcement for slabs
![]() Design of shear reinforcement for slabs
Design of shear reinforcement for slabs
Materials, Coefficients, Notation
The following notation for material parameters is used:
| Rbd | – | design compressive strength of concrete |
| Rbtd | – | design tensile strength of concrete |
| γu | – | coefficient of the shape of cross-section |
| z | – | lever arm (arm of internal forces) |
Coefficient γu is given by equation (Art. 5.2.2):
![]()
The most common notation for geometrical parameters:
| b | – | cross-section width |
| h | – | cross-section depth |
| he | – | effective depth of cross-section |
| z | – | lever arm (arm of internal forces) |
Verification of Rectangular Cross-Section Made of Plain Concrete
The cross-section is rectangular, loaded by the bending moment M, normal force N (applied in the cross-section centroid) and by the shear force Q. The cross-section bearing capacity subjected to bending moment is given by (Art. 5.2.5):
![]()
The shear strength is provided by (Art. 5.3.3, Appendix 9):
![]()
![]()
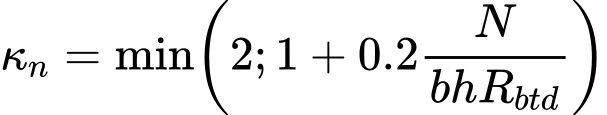
Strength of concrete cross-section subject to the combination of bending moment and normal force is derived from the following expressions depending on the normal force eccentricity e (Art. 5.2.5):
for:
![]()
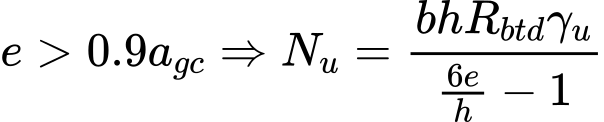
![]()
![]()
![]()
The ultimate bearing capacity is checket using the following formula (Art. 5.2.5.5):
![]()
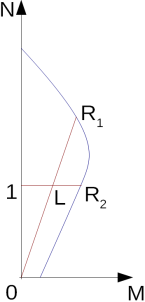 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R1| or |1L| / |1R2|. Where L is load, R1 is strength with prescribed eccentricity and R2 is strength with prescribed normal force.
Verification of Rectangular RC Cross-Section
The cross-section is rectangular, unilaterally reinforced and loaded by the bending moment and normal compression force. The program verifies a reinforced concrete section using the method of limit deformation (Art. 5.2.8). The maximum allowable strain of concrete in compression is 0.0025. Compression reinforcement is not taken into account.
The computed degree of reinforcement is checked using the following expressions (Art. 3.1.4.3, Art. 3.1.4.6):
![]()
![]()
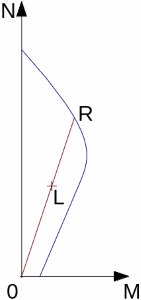 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed eccentricity.
Bending without normal force
The cross-section is rectangular, reinforced on one side and loaded by the bending moment Md.
The ultimate moment is provided by (Art. 5.2.7):
![]()
![]()
The program further checks whether the location of neutral axis x is less than the limit location of neutral axis xlim given by (Art. 5.2.7.1):
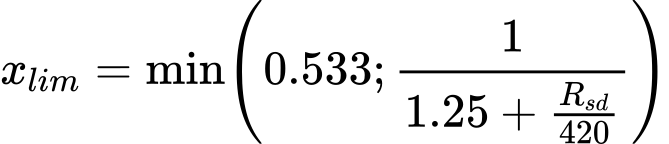
Shear
First, the program computes the ultimate shear strength of concrete Qbu (Art. 5.3.3, Appendix 9).
![]()
| where: | for: | h ≥ 0.3m | is: κq = 1.25 |
| for: | h > 0.15m | je κq = 1.50 | |
| for: | h < 0.15m | je κq = 1.60 |
If the ultimate shear strength of concrete is exceeded, the ultimate shear strength Qmax is checked (Art. 5.3.2.1).
![]()
Next, the necessary reinforcement area is given by (Art. 5.3.4):
![]()
where (Art. 5.3.5):
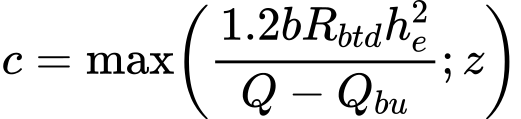
The magnitude of c is bounded by the following expression:
![]()
Verification of Circular RC Cross-Section
The program verifies a reinforced concrete pile using the method of limit deformation (Art. 5.2.8). The maximum allowable strain of concrete in compression is 0.0025. The degree of reinforcement is checked using the formula:
![]() Column – check for dominant compression (Art. 3.1.4.3, Art. 3.1.4.6)
Column – check for dominant compression (Art. 3.1.4.3, Art. 3.1.4.6)
![]()
![]()
![]() Beam – check for dominant bending
Beam – check for dominant bending
![]()
![]()
| where: | d | – | pile diameter |
| As | – | reinforcement area |
 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed eccentricity.
Shear
First, the program computes the ultimate shear strength of concrete Qbu (Art. 5.3.3, Appendix 9).
![]()
| where: | for: | 0.88d ≥ 0.3m | is: κq = 1.25 |
| for: | 0.88d > 0.15m | is: κq = 1.50 | |
| for: | 0.88d < 0.15m | is: κq = 1.60 |
If the ultimate shear strength of concrete is exceeded, the ultimate shear strength Qmax and strength of reinforced section Qu are checked (Art. 5.3.2.1).
![]()
![]()
where (Art. 5.3.5):
![]()
The magnitude of c is bounded by the following expression:
![]()
Verification of Spread Footing for Punching Shear
The program allows to verify spread footing for punching shear or for the design of shear reinforcement. The critical section loaded in shear Ucr is distant from the column edge by one half of the footing thickness. It is loaded by the prescribed moments Mx, My and by the shear force Qr provided by:
![]()
| where: | A | – | area of footing |
| Q | – | assigned vertical force developed in column | |
| At | – | hatched area in fig. |
 Dimensioning of shear reinforcement area At
Dimensioning of shear reinforcement area At
The program computes the maximal shear force Qdmax developed in the critical section, the shear force transmitted by concrete with no shear reinforcement Qbu, and the maximal allowable force Qmax:
![]()
![]()
where for: ![]() is:
is: ![]() or else:
or else: ![]()
![]()
![]()
For Qdmax < Qbu no shear reinforcement is needed.
For Qdmax > Qbuand Qdmax < Qmax the shear reinforcement must be introduced. The ultimate shear force is given by:
![]()
![]()
| where: | Ucr | – | critical cross-section span |
| α | – | is angle of bends | |
| As | – | overall area of bends in footing |
For Qdmax > Qmax the shear reinforcement cannot be designed. It is therefore necessary to increase the cross-section height.
Design of Longitudinal Reinforcement for Slabs
The design of reinforcement is performed for load caused by the bending moment M. The program provides the required area of tensile and compressive (if needed) reinforcement. It takes into account conditions for the minimum and maximum degree of reinforcement in a given cross-section. First, the program determines the location of neutral axis as:
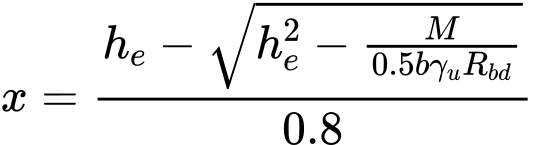
Providing the location of neutral axis is less than the allowable one (x < xlim), the program determines the area of tensile reinforcement Ast from the expression:
![]()
Providing the location of neutral axis is greater than the allowable one (x > xlim), the program determines the areas of both compressive Asc and tensile Ast reinforcement from the expressions:
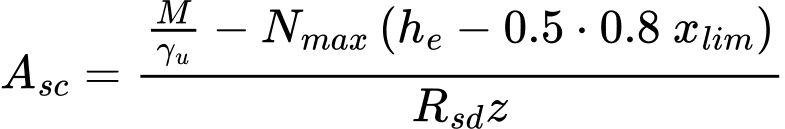
![]()
![]()
The limit location of neutral axis is found from:
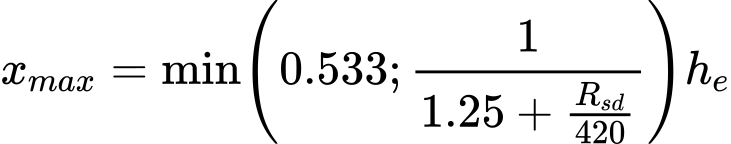
The computed degree of reinforcement is checked using the following expressions:
![]()
![]()
If the maximum degree of tensile reinforcement (μst,max = 0.03) or total reinforcement (μmax = 0.04), respectively, is exceeded, the program informs the user that the longitudinal reinforcement cannot be designed for a given cross-section.
Design of Shear Reinforcement for Slabs
The program allows determination of the required amount of shear reinforcement form by stirrups and bends, respectively.
First, the program computes the ultimate shear strength in a given section – the shear force transmitted by concrete Qbu and the maximum allowable shear force Qmax.
![]()
![]()
| where: | for: | h ≥ 0.3m | is: κq = 1.25 |
| for: | h > 0.15m | je κq = 1.50 | |
| for: | h < 0.15m | je κq = 1.60 |
As for stirrups the necessary reinforcement area is given by:
![]()
As for bends the necessary reinforcement area is given by:
![]()
where:
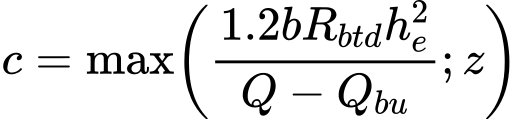
The magnitude of c is bounded by the following expression:
![]()
CSN 73 6206
When selecting “CSN 73 6206“, frame “Analysis methods”, the verification analysis of decisive joints is performed according to the standard CSN 73 6206 “Design of concrete and steel reinforced concrete bridge structures”, including changes a-10/1989 a Z2/1994. The program allows to verify cross sections from plain concrete or single-ended steel reinforced concrete. All calculations related to concrete are carried out using the theory of allowable stresses.
The main difference when compared to other standards appears in the dimensioning of concrete joints where the earth pressure is computed always without reduction of input parameters independently of the input in the frame “Settings”.
When performing the verification analysis of cross sections made either from plain or steel reinforced concrete it is possible input the coefficient of allowable stress according to art. 47 CSN 73 6206 to increase the material allowable stress.
The following joints can be verified by the program:
Abutment stem – foundation, construction joint – the cross section can be made either from plain or steel reinforced concrete. The joint is verified for the load due to normal force and bending moment. The allowable stresses of concrete, steel and concrete in concentric pressure are checked. In case of reinforced concrete the program also checks the degree of reinforcement, cross sections from plain concrete are then checked for overturning (h/2e < 1.35) and translation (N*f < 1.5); friction concrete-concrete is assumed as f = 0.5).
Closure wall – bearing block – the cross section is verified for the load due to normal force and bending moment. The steel reinforced concrete cross section is always assumed. The allowable stresses of concrete and steel and the degree of reinforcement are checked.
Wing wall – abutment – the joint can be made either from concrete or steel reinforced concrete. The allowable stresses of concrete, steel and concrete in concentric pressure are checked. In case of reinforced concrete the program also checks the degree of reinforcement.
Front jump of abutment foundation – the front jump of abutment is verified according to its projection. In case of jump projection v < 0.5hz (hz is the height of foundation jump) the program checks the magnitude of stress in principal tension due to forces developed in the above-foundation joint. The stress is determined as:
![]()
| where: | d | – | width of above-foundation joint |
| M,N | – | moment and normal force in above-foundation joint |
In case of jump projection v > 0.5hz the jump is analyzed as cantilever bended by the reaction (stress) of foundation soil. The joint can be made either from concrete or steel reinforced concrete. The allowable stresses of concrete, steel and concrete in concentric pressure are checked. In case of reinforced concrete the program also checks the degree of reinforcement.
PN-B-03264:2002
This help contains the following computationals methods:
![]() Materials, coefficients, notation
Materials, coefficients, notation
![]() Verification of rectangular cross-section made from plain concrete
Verification of rectangular cross-section made from plain concrete
![]() Verification of rectangular RC cross-section
Verification of rectangular RC cross-section
![]() Verification of circular RC cross-section
Verification of circular RC cross-section
![]() Verification of spread footing for punching shear
Verification of spread footing for punching shear
![]() Design of longitudinal reinforcement for slabs
Design of longitudinal reinforcement for slabs
![]() Design of shear reinforcement for slabs
Design of shear reinforcement for slabs
Materials, Coefficients, Notation
The following notation for material parameters is used:
| fck | – | characteristic compressive strength of concrete |
| fcd | – | design compressive strength of concrete |
| fctk | – | characteristic tensile strength of concrete |
| fctd | – | design tensile strength of concrete |
| fyk | – | characteristic tensile strength of steel bar |
| fyd | – | design tensile strength of steel bar |
| fctm | – | mean tensile strength of steel bar |
![]()
![]()
![]()
![]()
| where: | αcc = 1 | ||
| αct = 1 | |||
| γc = 1.5 | – | for reinforced concrete structures | |
| γc = 1.8 | – | for concrete strustures |
The most common notation for geometrical parameters:
| where: | b | – | cross-section width |
| h | – | cross-section depth | |
| d | – | effective depth of cross-section | |
| z | – | lever arm (arm of internal forces) |
Verification of Rectangular Cross-Section Made of Plain Concrete
The cross-section is rectangular, loaded by the bending moment MSd, normal force NSd (applied in the cross-section centroid) and by the shear force VSd. The cross-section bearing capacity subjected to bending moment is given by:
![]()
The shear strength is provided by:
![]()
where:
![]()
Strength of concrete cross-section subject to the combination of bending moment and normal force is derived from the following expressions depending on the normal force eccentricity e:
As the greater of:
![]()
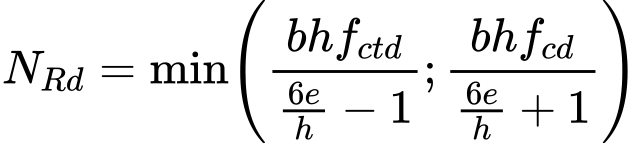
where:
![]()
![]()
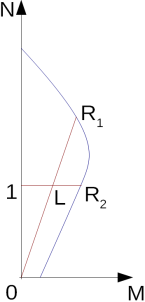 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R1| or |1L| / |1R2|. Where L is load, R1 is strength with prescribed eccentricity and R2 is strength with prescribed normal force.
Verification of Rectangular RC Cross-Section
The cross-section is rectangular, unilaterally reinforced and loaded by the bending moment and normal compression force. The program verifies a reinforced concrete section using the method of limit deformation. The maximum allowable strain of concrete in compression is 0.002 – 0.0035. Compression reinforcement is not taken into account.
The computed degree of reinforcement is checked using the following expressions:
![]()
where:
![]()
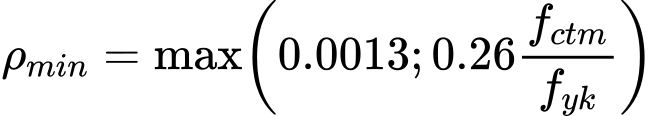
![]()
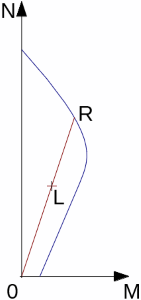 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed eccentricity.
Bending without normal force
The cross-section is rectangular, reinforced on one side and loaded by the bending moment MSd.
The permissible moment for a given area of reinforcements As reads:
![]()
![]()
The program further checks whether the location of neutral axis x is less than the limit location of neutral axis xlim given by:
![]()
where:
![]()
![]()
Shear
First, the program computes the ultimate shear strength of concrete VRd1.
![]()
where:
![]()
![]()
If the ultimate shear strength of concrete is exceeded, the ultimate shear strength VRd2 is checked.
![]()
where:
![]()
Next, the necessary reinforcement area is given by:
![]()
Verification of Circular RC Cross-Section
The program verifies a reinforced concrete pile using the method of limit deformation. The maximum allowable strain of concrete in compression is 0,002 – 0,0035. The degree of reinforcement is checked using the formula:
![]()
![]() Column – check for dominant compression
Column – check for dominant compression
![]()
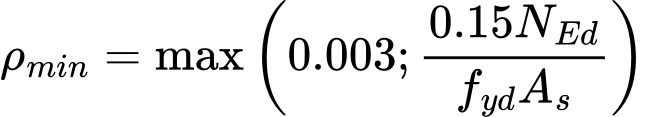
![]()
![]() Beam – check for dominant bending
Beam – check for dominant bending
![]()
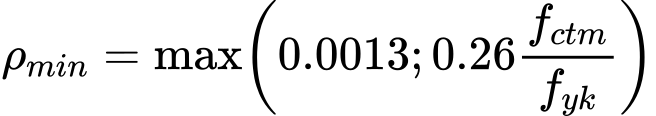
![]()
| where: | d | – | pile diameter |
| As | – | reinforcement area |
 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed eccentricity.
Verification of Spread Footing for Punching Shear
The critical section loaded in shear u is distant from the column edge by one half of the footing thickness. It is loaded by the prescribed moments Mx, My and by the shear force NSd provided by:
![]()
| where: | A | – | area of footing |
| V | – | assigned vertical force developed in column | |
| At | – | hatched area in fig. |
 Dimensioning of shear reinforcement area At
Dimensioning of shear reinforcement area At
The program computes the maximal shear force NSd developed in the critical section, the shear force transmitted by concrete with no shear reinforcement NRd1 and the maximal allowable force NRd,max:
![]()
![]()
For NSd < NRd no shear reinforcement is needed.
For NSd >NRd and NSd < NRd,max the shear reinforcement must be introduced. The ultimate shear force is given by:
![]()
| where: | u | – | critical cross-section span |
| α | – | is angle of bends | |
| Asw | – | overall area of bends in footing |
For NSd >NRd,max the shear reinforcement cannot be designed. It is therefore necessary to increase the cross-section height.
Design of Longitudinal Reinforcement for Slabs
The design of reinforcement is performed for load caused by the bending moment MSd. The program provides the required area of tensile and compressive (if needed) reinforcement. It takes into account conditions for the minimum and maximum degree of reinforcement in a given cross-section. First, the program determines the location of neutral axis as:
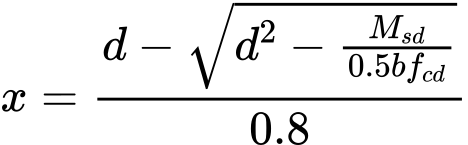
Providing the location of neutral axis is less than the allowable one (x < xmax), the program determines the area of tensile reinforcement Ast from the expression:
![]()
Providing the location of neutral axis is greater than the allowable one (x > xmax), the program determines the areas of both compressive Asc and tensile Ast reinforcement from the expressions:
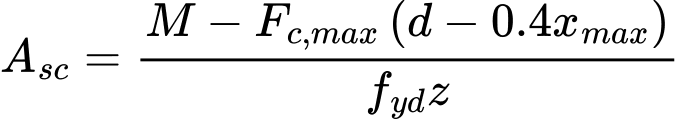
![]()
![]()
The limit location of neutral axis is found from:
![]()
where:
![]()
![]()
The computed degree of reinforcement is checked using the following expressions:
![]()
where:
![]()
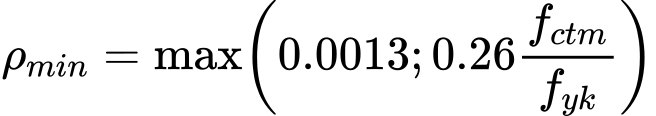
![]()
If the maximum degree of total reinforcement ρmax is exceeded, the program informs the user that the longitudinal reinforcement cannot be designed for a given cross-section.
Design of Shear Reinforcement for Slabs
The program allows determination of the required amount of shear reinforcement form by stirrups and bends, respectively.
First, the program computes the ultimate shear strength in a given section – the shear force transmitted by concrete VRd1 and the maximum allowable shear force VRd2.
![]()
where:
![]()
![]()
![]()
where:
![]()
As for stirrups the necessary reinforcement area is given by:
![]()
As for bends the necessary reinforcement area is given by:
![]()
BS 8110:1997
This help contains the following computationals methods:
![]() Materials, coefficients, notation
Materials, coefficients, notation
![]() Verification of rectangular cross-section made of plain concrete
Verification of rectangular cross-section made of plain concrete
![]() Verification of rectangular RC cross-section
Verification of rectangular RC cross-section
![]() Verification of circular RC cross-section
Verification of circular RC cross-section
![]() Verification of spread footing for punching shear
Verification of spread footing for punching shear
![]() Design of longitudinal reinforcement for slabs
Design of longitudinal reinforcement for slabs
![]() Design of shear reinforcement for slabs
Design of shear reinforcement for slabs
Materials, Coefficients, Notation
The following notation for material parameters is used:
| fcu | – | characteristic strength of concrete |
| fy | – | characteristic strength of reinforcement |
| fyd | – | design strength of steel in tension |
![]()
The characteristic compressive strength of concrete is the basic input parameter given by the class of concrete.
The most common notation for geometrical parameters:
| b | – | cross-section width |
| h | – | cross-section depth |
| d | – | effective depth of cross-section |
| z | – | lever arm (arm of internal forces) |
All computations are carried out according to the theory of limit states.
Verification of Rectangular Cross-Section Made of Plain Concrete
The cross-section is rectangular, loaded by the bending moment M, normal force N (applied in the cross-section centroid) and by the shear force V.
Strength of concrete cross-section subject to the combination of bending moment and normal force with eccentricity e is derived from the following expressions:
![]()
![]()
![]()
The shear strength is provided by:
![]()
| where: | νc | – | is the design value of shear stress in concrete for degree of longitudinal reinforcement ρ = 0 (see: Verification of spread footing for punching shear) |
 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R1| or |1L| / |1R2|. Where L is loading, R1 is strength with prescribed eccentricity and R2 is strength with prescribed normal force.
Verification of Rectangular RC Cross-Section
The cross-section is rectangular, unilaterally reinforced and loaded by the bending moment and normal compression force. The program verifies a reinforced concrete section using the method of limit deformation. The maximum allowable strain of concrete in compression is 0,002 – 0,0035. Compression reinforcement is not taken into account. Minimum eccentricity is applied:
![]()
The computed degree of reinforcement is checked using the following expressions:
| where: | ||
| – for fy = 460 N/mm2 | ||
| – for fy = 250 N/mm2 | ||
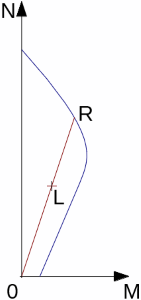 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed eccentricity.
Bending without normal force
The cross-section is rectangular, reinforced on one side and loaded by the bending moment Mu.
The permissible moment for a given area of reinforcements As reads:
![]()
![]()
![]()
The program further checks whether the location of neutral axis x is less than the limit location of neutral axis xmax given by:
![]()
Shear
First, the program computes the ultimate shear strength of concrete Vc.
![]()
where:
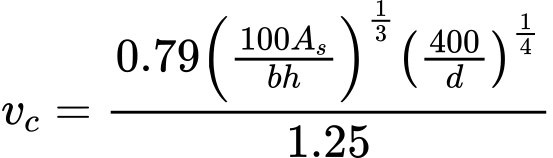
The νc values are for fcu above 25 N/mm2 multiplied by (fcu / 25)1/3
If the ultimate shear strength of concrete is exceeded, the ultimate shear strength Vmax is checked.
![]()
Next, the necessary reinforcement area is given by:
![]()
where:
![]()
Verification of Circular RC Cross-Section
The program verifies a reinforced concrete pile using the method of limit deformation. The maximum allowable strain of concrete in compression is 0,002 – 0,0035.
The degree of reinforcement is checked using the formula:
![]()
![]() Column – check for dominant compression
Column – check for dominant compression
| ρmax = 0,04 | ||
| ρmin = 0,0013 | – for fy = 460 N/mm2 | |
| ρmin = 0,0024 | – for fy = 250 N/mm2 | |
![]() Beam – check for dominant bending
Beam – check for dominant bending
| ρmax = 0,06 | ||
| ρmin = 0,004 | ||
| where: | d | – | pile diameter |
| As | – | reinforcement area |
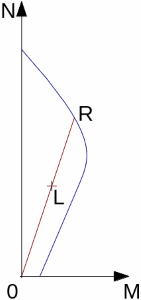 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed eccentricity.
Verification of Spread Footing for Punching Shear
The critical section loaded in shear Ucr is distant from the column edge by one half of the footing thickness. It is loaded by the prescribed moments Mx, My and by the shear force V provided by:
![]()
| where: | A | – | area of footing |
| Q | – | assigned vertical force developed in column | |
| At | – | hatched area in fig. |
 Dimensioning of shear reinforcement area At
Dimensioning of shear reinforcement area At
The program computes the maximum shear force V developed in the critical section, the shear force transmitted by concrete with no shear reinforcement Vc, and the maximal allowable force Vu:
![]()
![]()
where:
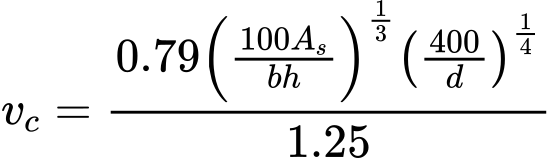
The νc values are for fcu above 25 N/mm2 multiplied by (fcu / 25)1/3
| where: | νu | – | is ultimate shear stress |
For V < Vc no shear reinforcement is needed.
For V > Vcand Vc < Vu it is necessary to design shear reinforcement. The permissable shear force is given by:
![]()
![]()
![]()
| where: | u | – | critical cross-section span |
| α | – | angle of bends | |
| Aus | – | overall area of bends in footing |
For V > Vu the shear reinforcement cannot be designed. It is therefore necessary to increase the cross-section depth.
Design of Longitudinal Reinforcement for Slabs
The design of reinforcement is performed for load caused by the bending moment Md. The program provides the required area of tensile and compressive (if needed) reinforcement. It takes into account conditions for the minimum and maximum degree of reinforcement in a given cross-section. First, the program determines the location of neutral axis as:
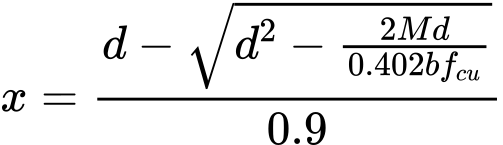
Providing the location of neutral axis is less than the allowable one (x < xmax), the program determines the area of tensile reinforcement Ast from the expression:
![]()
Providing the location of neutral axis is greater than the allowable one (x > xmax), the program determines the areas of both compressive Asc and tensile Ast reinforcement from the expressions:
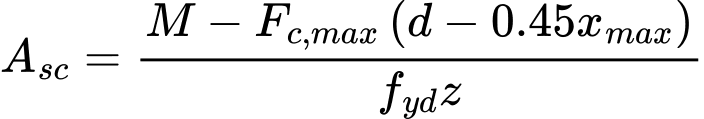
![]()
![]()
The limit location of neutral axis is found from:
![]()
The computed degree of reinforcement is checked using the following expressions:
| where: | ||
| – for fy = 460 N/mm2 | ||
| – for fy = 250 N/mm2 | ||
If the maximum degree of reinforcement ρmax is exceeded, the program informs the user that the longitudinal reinforcement cannot be designed for a given cross-section.
Design of Shear Reinforcement for Slabs
The program allows determination of the required amount of shear reinforcement form by stirrups and bends, respectively.
First, the program computes the ultimate shear strength in a given section – the shear force transmitted by concrete Vc and the maximum allowable shear force Vmax.
![]()
where:
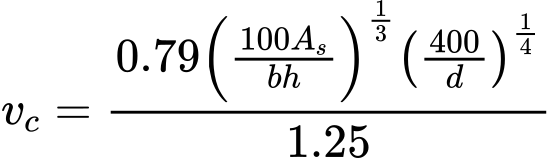
The νc values are for fcu above 25 N/mm2 multiplied by (fcu / 25)1/3
![]()
As for stirrups the necessary reinforcement area is given by:
![]()
As for bends the necessary reinforcement area is given by:
![]()
where:
![]()
IS 456
This help contains the following computationals methods:
![]() Materials, coefficients, notation
Materials, coefficients, notation
![]() Verification of rectangular cross-section made of plain concrete
Verification of rectangular cross-section made of plain concrete
![]() Verification of rectangular RC cross-section
Verification of rectangular RC cross-section
![]() Verification of circular RC cross-section
Verification of circular RC cross-section
![]() Verification of spread footing for punching shear
Verification of spread footing for punching shear
![]() Design of longitudinal reinforcement for slabs
Design of longitudinal reinforcement for slabs
![]() Design of shear reinforcement for slabs
Design of shear reinforcement for slabs
Materials, Coefficients, Notation
The following notation for material parameters is used:
| fck | – | characteristic cube compressive strength of concrete |
| fcd | – | design compressive strength of concrete |
| fctk | – | characteristic tensile strength of concrete |
| fctd | – | design tensile strength of concrete |
| fy | – | characteristic strength of steel bar |
| fyd | – | design tensile strength of steel bar |
The characteristic compressive strength of concrete is the basic input parameter given by the class of concrete – it serves to derive the remaining coefficients of reliability.
![]()
![]()
![]()
![]()
![]()
The most common notation for geometrical parameters:
| b | – | cross-section width |
| h | – | cross-section depth |
| d | – | effective depth of cross-section |
| z | – | lever arm (arm of internal forces) |
All computations are carried out according to the theory of limit states.
Verification of Rectangular Cross-Sections Made of Plain Concrete
The cross-section is rectangular, loaded by the bending moment M, normal force N (applied in the cross-section centroid) and by the shear force V:
![]()
The shear strength is provided by:
![]()
| where: | τc | – | is the design value of stress in concrete obtained from table 19 of the IS456 standard for degree of longitudinal reinforcement ρ = 0. |
Strength of concrete cross-section subject to the combination of bending moment and normal force with eccentricity e is derived from the following expressions:
![]()
where:
![]()
![]()
 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R1| or |1L| / |1R2|. Where L is load, R1 is strength with prescribed eccentricity and R2 is strength with prescribed normal force.
Verification of Rectangular RC Cross-Section
The cross-section is rectangular, unilaterally reinforced and loaded by the bending moment and normal compression force. The program verifies a reinforced concrete section using the method of limit deformation. The maximum allowable strain of concrete in compression is 0.002 – 0.0035. Compression reinforcement is not taken into account. Minimum eccentricity is applied:
![]()
The computed degree of reinforcement is checked using the following expressions:
![]()
![]()
![]()
![]()
 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed eccentricity.
Bending without normal force
The cross-section is rectangular, reinforced on one side and loaded by the bending moment M.
The permissible moment for a given area of reinforcements As reads:
![]()
![]()
![]()
The program further checks whether the location of neutral axis x is less than the limit location of neutral axis xmax given by:
| xmax = 0.53d | – for steel Fe 250 |
| xmax = 0.48d | – for steel Fe 400 |
| xmax = 0.46d | – for steel Fe 500 |
Shear
First, the program computes the ultimate shear strength of concrete Vuc.
![]()
where: τc is determined according to table 19 standard IS 456 : 2000.
If the ultimate shear strength of concrete is exceeded, the ultimate shear strength Vuc,max is checked.
![]()
where: τc,max is determined according to table 20 standard IS 456 : 2000.
Next, the necessary reinforcement area is given by:
![]()
where:
![]()
Verification of Circular RC Cross-Section
The program verifies a reinforced concrete pile using the method of limit deformation. The maximum allowable strain of concrete in compression is 0.002 – 0.0035.
The degree of reinforcement is checked using the formula:
![]()
![]() Column – check for dominant compression
Column – check for dominant compression
![]()
![]()
![]()
![]() Beam – check for dominant bending
Beam – check for dominant bending
![]()
![]()
![]()
| where: | d | – | pile diameter |
| As | – | reinforcement area |
 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed eccentricity.
Verification of Spread Footing for Punching Shear
The critical section loaded in shear Ucr is distant from the column edge by one half of the footing thickness. It is loaded by the prescribed moments Mx, My and by the shear force Vr provided by:
![]()
| where: | A | – | area of footing |
| Q | – | assigned vertical force developed in column | |
| At | – | hatched area in fig. |
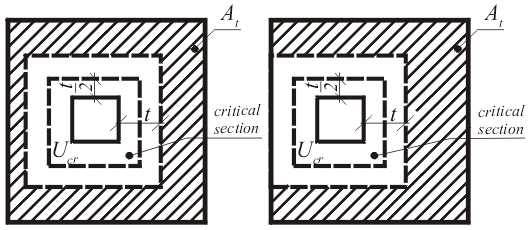 Dimensioning of shear reinforcement area At
Dimensioning of shear reinforcement area At
The program computes the maximum shear force V developed in the critical section, the shear force transmitted by concrete with no shear reinforcement Vc, and the maximal allowable force Vmax:
![]()
![]()
where:
![]()
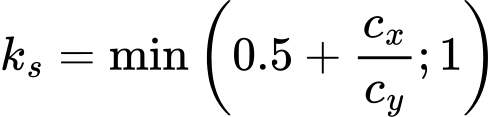
where: cx, cy – are dimensions of footing column
For V < Vc no shear reinforcement is needed.
For V > Vc and V< Vmax it is necessary to design shear reinforcement. The permissable shear force is given by:
![]()
![]()
| where: | u | – | critical cross-section span |
| α | – | is angle of bends | |
| Asv | – | overall area of bends in footing |
For V > Vmax the shear reinforcement cannot be designed. It is therefore necessary to increase the cross-section depth.
Design of Longitudinal Reinforcement for Slabs
The design of reinforcement is performed for load caused by the bending moment Mrd. The program provides the required area of tensile and compressive (if needed) reinforcement. It takes into account conditions for the minimum and maximum degree of reinforcement in a given cross-section. First, the program determines the location of neutral axis as:
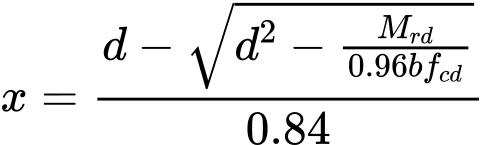
Providing the location of neutral axis is less than the allowable one (x < xmax), the program determines the area of tensile reinforcement Ast from the expression:
![]()
Providing the location of neutral axis is greater than the allowable one (x > xmax), the program determines the areas of both compressive Asc and tensile Ast reinforcement from the expressions:
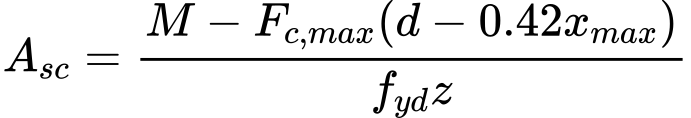
![]()
![]()
The limit location of neutral axis is found from:
| xmax = 0.53d | for steel Fe 250 |
| xmax = 0.48d | for steel Fe 400 |
| xmax = 0.46d | for steel Fe 500 |
The computed degree of reinforcement is checked using the following expressions:
![]()
![]()
![]()
![]()
If the maximum degree of tensile reinforcement (ρt,max = 0.04) or total reinforcement (ρmax = 0.08), respectively, is exceeded, the program informs the user that the longitudinal reinforcement cannot be designed for a given cross-section.
Design of Shear Reinforcement for Slabs
The program allows determination of the required amount of shear reinforcement form by stirrups and bends, respectively.
First, the program computes the ultimate shear strength in a given section – the shear force transmitted by concrete Vcu and the maximum allowable shear force Vuc,max.
![]()
where: τc is determined according to table 19 standard IS 456 : 2000.
![]()
where: τc,max is determined according to table 20 standard IS 456 : 2000.
As for stirrups the necessary reinforcement area is given by:
![]()
As for bends the necessary reinforcement area is given by:
![]()
where:
![]()
ACI 318-11
Esta ajuda contém os seguintes métodos:
![]() Materiais, coeficientes, notações
Materiais, coeficientes, notações
![]() Verificação da secção transversal retangular realizada em concreto liso
Verificação da secção transversal retangular realizada em concreto liso
![]() Verificação da secção transversal retangular em concreto armado
Verificação da secção transversal retangular em concreto armado
![]() Verificação da secção transversal circular em concreto armado
Verificação da secção transversal circular em concreto armado
![]() Verificação da sapata para o punçoamento
Verificação da sapata para o punçoamento
![]() Dimensionamento de armadura longitudinal para lajes
Dimensionamento de armadura longitudinal para lajes
![]() Dimensionamento de armadura transversal para lajes
Dimensionamento de armadura transversal para lajes
Materiais, Coeficientes, Notações
É utilizada a seguinte notação para os parâmetros materiais:
| f’c | – | resistência específica à compressão do concreto |
| Ec | – | módulo de elasticidade |
| fy | – | tensão de cedência do aço |
O módulo de elasticidade é dado por (Art. 8.5.1):
![]()
A notação mais comum para parâmetros geométricos é dada por:
| b | – | largura da secção transversal |
| h | – | profundidade da secção transversal |
| d | – | profundidade efetiva da secção transversal |
Verificação da Secção Transversal Retangular realizada em Concreto Liso
A secção transversal retangular, carregada pelo momento M, força normal P (aplicada no centroide da secção transversal) e pela força transversal Vn.
A resistência ao cisalhamento é dada por (Art. 22.5.4, Art. 9.3.5):
![]()
![]()
![]()
A resistência da secção transversal em concreto sujeita à combinação de momento fletor e força normal é derivada a partir das expressões seguintes (Art. 22.5.3, Art. 9.3.5):
para a parte comprimida:
![]()
onde:
![]()
![]()
![]()
![]()
para a parte tracionada:
![]()
onde:
![]()
Verificação da Secção Transversal Retangular em Concreto Armado
A secção é retangular, com armadura unilateral e carregada pelo momento fletor e força normal de compressão. O programa verifica uma secção de concreto armada através do método da deformação limite (Art. 10.3, Art.10.4). A deformação máxima permitida do concreto à compressão 0,003. A armadura de compressão não é considerada.
O índice computado de armadura é verificado através das expressões seguintes (Art. 10.5.1):
![]()
![]()
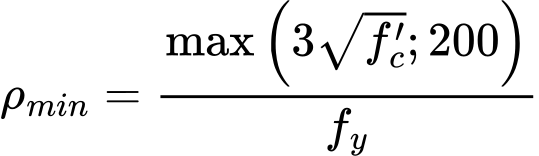
 Diagrama de interação N-M
Diagrama de interação N-M
O rácio de utilização da secção transversal de concreto sujeita à combinação de momento fletor e força normal é determinado através de |0L| / |0R|. Onde L é o carregamento e R é a resistência para a excentricidade definida.
Flexão sem força normal
A secção transversal é retangular, com armadura de um dos lados, e carregada pelo momento fletor Mu.
O momento último é dado por (Cap. 10, Art. 10.2.7.3, Art. 9.3.2.1):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A posição limite do eixo neutro é dada por:
![]()
Cisalhamento
Primeiro, o programa computa a resistência ao cisalhamento última do concreto Vc (Art. 11.2.1.1).
![]()
Caso a resistência ao cisalhamento última do concreto seja excedida, verifica-se a resistência ao cisalhamento última Vmax (Art. 11.2.1.1 + Art. 11.4.7.9).
![]()
De seguida, a área de armadura necessária é dada por (Art. 11.4.7):
![]()
onde (Art. 11.4.2, Art. 9.3.2.3):
![]()
![]()
Verificação da Secção Transversal Circular em Concreto Armado
O programa verifica a estaca de concreto armada através do método da deformação limite (Art. 10.3, Art. 10.4). A deformação máxima permitida para o concreto à compressão é 0,003. O índice de armadura é verificado através da formula:
![]()
![]() Pilar – verificação da compressão dominante (Art. 10.9.1)
Pilar – verificação da compressão dominante (Art. 10.9.1)
![]()
![]()
![]()
![]() Viga – verificação da flexão dominante (Art. 10.5.1)
Viga – verificação da flexão dominante (Art. 10.5.1)
![]()
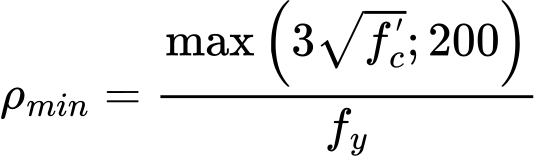
| onde: | d | – | diâmetro da estaca |
| As | – | área de armadura |
 Diagrama de interação N-M
Diagrama de interação N-M
O rácio de utilização da secção transversal de concreto sujeita à combinação de momento fletor e força normal é determinado através de |0L| / |0R|. Onde L é o carregamento e R é a resistência para a excentricidade definida.
Cisalhamento
Primeiro, o programa computa a resistência ao cisalhamento última do concreto Vc (Art. 11.2.1.1, Art. 11.2.3).
![]()
Caso a resistência ao cisalhamento última do concreto seja excedida, verifica-se a resistência ao cisalhamento última Vmax e a resistência da secção armada Vs (Art. 11.2.1.1 + Art. 11.4.7.9, Art. 11.2.3, Art. 11.4.7.2).
![]()
![]()
onde (Art. 11.4.2, Art. 9.3.2.3):
![]()
![]()
Verificação da Sapata para o Punçoamento
O programa permite verificar a sapata para o punçoamento ou para a armadura de punçoamento dimensionada. A secção crítica carregada transversalmente bo está afastada da extremidade do pilar por metade da espessura da sapata. Esta é carregada pelos momentos Mx, My e pela força de cisalhamento Vu, que são dados por:
![]()
| onde: | A | – | área da sapata |
| V | – | força vertical definida ao longo do pilar | |
| At | – | área sombreada da figura |
 Dimensionamento da área de armadura transversal At
Dimensionamento da área de armadura transversal At
O programa computa a força de cisalhamento máxima Vu desenvolvida na secção crítica, a força de cisalhamento transmitida pelo concreto sem armadura transversal Vc como valores mínimos (Art. 11.11.2.1):
![]()
onde βc representa o rácio de esbelteza do pilar.
![]()
| onde αs = | 40 | – | pilar interior |
| 30 | – | pilar de extremidade | |
| 20 | – | pilar de esquina |
![]()
a força máxima permitida Vmax (Art. 11.11.3.2):
![]()
Para Vu < ϕ×Vc não é necessária armadura transversal.
Para Vu > ϕ×Vc e Vu < ϕ×Vmax é necessária armadura transversal. A força de cisalhamento última é dada por (Art. 11.11.3.1):
![]()
![]()
| onde: | bo | – | vão da secção transversal crítica |
| α | – | ângulo de curvatura | |
| Av | – | área total de curvatura da sapata |
Para Vu > ϕ×Vmax não é possível dimensionar armadura transversal. Neste caso, é necessário aumentar a altura da secção transversal.
Dimensionamento de Armadura Longitudinal para Lajes
O dimensionamento de armadura é realizado em função do carregamento devido ao momento fletor M. O programa fornece a área necessário de armadura de tração e compressão (caso necessária). As condições para o rácio de armadura mínimo e máximo de uma dada secção transversal são consideradas. Primeiro, o programa determina a posição do eixo neutro através de:
Caso a posição do eixo neutro seja inferior ao permitido (x < xlim), o programa determina a área de armadura de tração Ast através da expressão:
![]()
Caso a posição do eixo neutro seja superior ao permitido (x > xlim), o programa determina as áreas de armadura de compressão Asc e de tração Ast através das expressões:
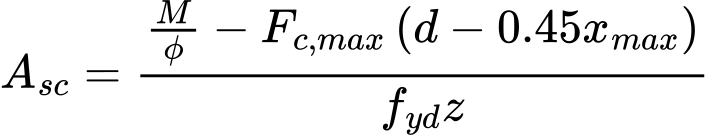
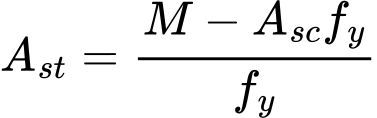
![]()
onde:
![]()
A posição limite do eixo neutro é dada por:
![]()
O rácio de armadura computado é verificado através das expressões seguintes:
![]()
![]()
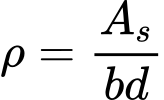
Dimensionamento de Armadura Transversal para Lajes
O programa permite a determinação da armadura transversal necessária a partir de estribos e remates.
Primeiro, o programa computa a resistência de cisalhamento última para uma dada secção – a força transversal transmitida pelo concreto Vc (Art. 11.2.1.1) e a força transversal máxima permitida Vmax (Art. 11.2.1.1 + Art. 11.4.7.9).
![]()
![]()
Para os estribos, a área de armadura necessária é dada por (Art. 11.4.7.2):
![]()
Para os remates, a área de armadura necessária é dada por (Art. 11.4.7.4):
![]()
onde (Art. 11.4.2, Art. 9.3.2.3):
![]()
![]()
AS 3600 – 2018
This help contains the following computationals methods:
![]() Materials, coefficients, notation
Materials, coefficients, notation
![]() Verification of rectangular cross-section made of plain concrete
Verification of rectangular cross-section made of plain concrete
![]() Verification of rectangular RC cross-section
Verification of rectangular RC cross-section
![]() Verification of circular RC cross-section
Verification of circular RC cross-section
![]() Verification of spread footing for punching shear
Verification of spread footing for punching shear
![]() Design of longitudinal reinforcement for slabs
Design of longitudinal reinforcement for slabs
![]() Design of shear reinforcement for slabs
Design of shear reinforcement for slabs
Materials, Coefficients, Notation
The following notation for material parameters is used:
| f ‘c | – | characteristic compressive cylinder strength of concrete at 28 days |
| Ec | – | mean value of the modulus of elasticity of concrete at 28 days |
| f ‘ct,f | – | characteristic flexural tensile strength of concrete |
| f ‘ct | – | characteristic principal tensile strength of concrete |
| fsy | – | yield strength of reinforcing steel |
![]()
![]()
The characteristic compressive strength of concrete is the basic input parameter given by the class of concrete.
The most common notation for geometrical parameters:
| b | – | cross-section width |
| D | – | cross-section depth |
| d | – | effective depth of cross-section |
| z | – | lever arm (arm of internal forces) |
All computations are carried out according to the theory of limit states.
Verification of Rectangular Cross-Sections Made of Plain Concrete
The cross section is rectangular, loaded by the bending moment M, normal force N (applied in the cross section centroid) and by the shear force V. The cross section bearing capacity subjected to bending moment is given by (Art. 20.4.2, 2.2.2):
The shear strength is provided by (Art. 20.4.3):
![]()
![]()
![]()
Strength of concrete cross section subject to the combination of bending moment and normal force is derived from the following expressions depending on the normal force eccentricity e ≥ 0.05D (Art. 10.1.2, 20.4.2, 2.2.2):
![]()
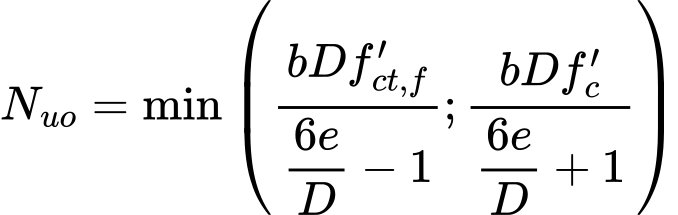
where:
![]()
![]()
 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross section subject to the combination of bending moment and normal force is determined as |0L| / |0R1| or |1L| / |1R2|. Where L is load, R1 is strength with prescribed eccentricity and R2 is strength with prescribed normal force.
Verification of Rectangular RC Cross-Section
The cross-section is rectangular, unilaterally reinforced and loaded by the bending moment and normal compression force. The program verifies a reinforced concrete section using the method of limit deformation (Art. 8.1). The maximum allowable strain of concrete in compression is 0.003. Compression reinforcement is not taken into account.
The computed degree of reinforcement is checked using the following expressions:
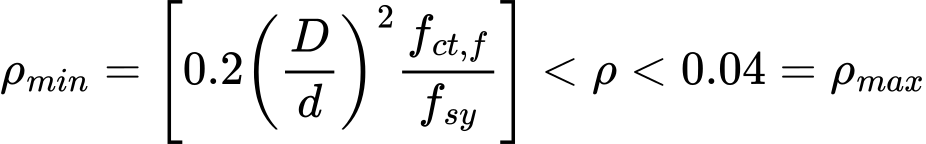
![]()
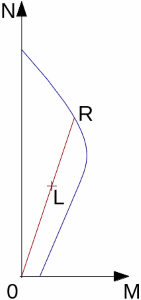 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed excentricity.
Bending without normal force
The cross-section is rectangular, reinforced on one side and loaded by the bending moment M.
The permissible moment for a given area of reinforcements As reads:
![]()
for L class reinforcement (Art. 2.2.2):
![]()
for N class reinforcement:
![]()
kde
![]()
![]()
![]()
![]()
The program further checks whether the neutral axis parameter ku is less than the limit value (Art 8.1.5) :
![]()
![]()
Shear
First, the program computes the ultimate shear strength of concrete Vuc (Art. 8.2.4.1).
![]()
where (Art. 8.2.1.9, Art. 8.2.4.3):
![]()
![]()
![]()
If the ultimate shear strength of concrete is exceeded, the ultimate shear strength Vu,max is checked (Art. 8.2.3.3).
![]()
![]()
Next, the necessary reinforcement area is given by (Art. 8.2.5.2):
![]()
where:
![]()
Verification of Circular RC Cross-Section
The program verifies a reinforced concrete pile using the method of limit deformation (Art 10.6.1). The maximum allowable strain of concrete in compression is 0.003.
The degree of reinforcement is checked using the formula:
![]()
![]() Column – check for dominant compression (Art. 10.7.1)
Column – check for dominant compression (Art. 10.7.1)
![]()
![]()
![]()
![]() Beam – check for dominant bending (Art. 8.1.6.1)
Beam – check for dominant bending (Art. 8.1.6.1)
![]()
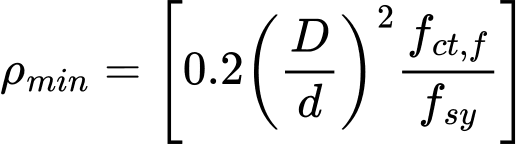
![]()
| where: | d | – | pile diameter |
| As | – | cross sectional area of reinforcement |
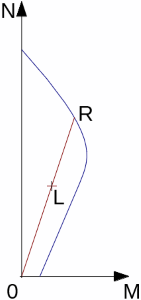 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed excentricity.
Shear
![]()
![]()
First, the program computes the ultimate shear strength of concrete Vc. Formulas are from Art. 8.2.4.1, where the section width (bv) is replaced by 0.88d and effective depth (dv) is replaced 0.8*0.9*0.9d.
![]()
where (Art. 8.2.1.9, Art. 8.2.4.3):
![]()
![]()
If the ultimate shear strength of concrete is exceeded, the ultimate shear strength Vu,max and strength of reinforced section Vus are checked (Art. 8.2.5.2).
![]()
![]()
![]()
Verification of Spread Footing for Punching Shear
The program allows to verify spread footing for punching shear. The critical section loaded in shear Ucr is distant from the column edge by one half of the footing thickness. It is loaded by the prescribed moments Mx, My and by the shear force V* provided by:
![]()
| where: | A | – | area of footing |
| V | – | assigned vertical force developed in column | |
| At | – | hatched area in fig. |
 Dimensioning of shear reinforcement area At
Dimensioning of shear reinforcement area At
The program computes the maximal shear force V* developed in the critical section, the shear force transmitted by concrete with no shear reinforcement Vuc as minimum of values (Art. 9.3.3):
![]()
![]()
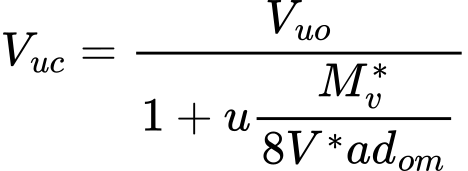
where:
![]()
![]()
where βc is the ratio of the longest overall dimension of the effective loaded area, Y, to the overall dimension, X, measured perpendicular to Y.
and the maximal allowable force Vumax (Art. 9.3.4):
![]()
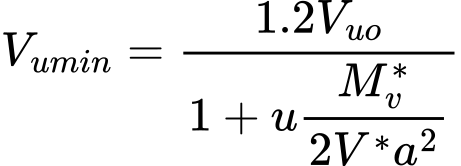
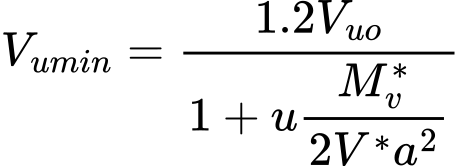
| where: | u | – | critical cross section span |
| x | – | short dimension of cross section | |
| y | – | long dimension of cross section | |
| a | – | the dimension of the critical shear perimeter measured parallel to the direction of M*v | |
| M*v | – | the bending moment transferred from the slab to a support in the direction being considered |
For V* < Vuc no shear reinforcement is needed.
For V* > Vuc and V* < Vumax the shear reinforcement must be introduced. The ultimate shear force is given by (Art. 9.3.4):
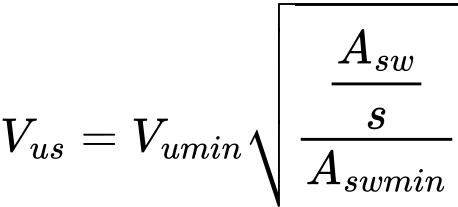
![]()
Area of reinforcement must satisfy condition (Art. 9.3.4):
![]()
For V* > Vumax the shear reinforcement cannot be designed. It is therefore necessary to increase the cross section height.
The analysis is carried out independently in directions x and y, as the decisive one the lower value of Vu is accepted.
Design of Longitudinal Reinforcement for Slabs
The design of reinforcement is performed for load caused by the bending moment M. The program provides the required area of tensile and compressive (if needed) reinforcement. It takes into account conditions for the minimum and maximum degree of reinforcement in a given cross section. First, the program determines the location of neutral axis as (Art. 8.1):
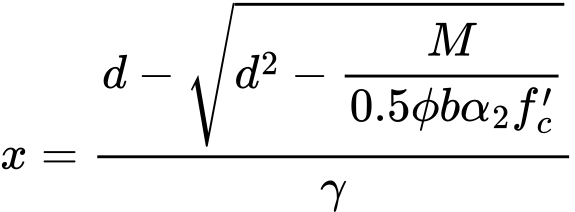
where:
![]()
![]()
for L class reinforcement (Art. 2.2.2):
![]()
for N class reinforcement:
![]()
Providing the location of neutral axis is less than the allowable one (xmax), the program determines the area of tensile reinforcement Ast from the expression:
![]()
Providing the location of neutral axis is greater than the allowable one (xmax), the program determines the areas of both compressive (Asc) and tensile (Ast) reinforcement from the expressions:
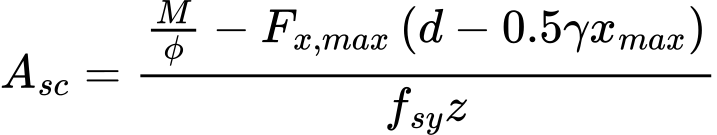
![]()
![]()
The limit location of neutral axis xmax is found from (Art. 8.1.5):
![]()
The computed degree of reinforcement is checked using the following expressions (Art. 10.5.1.2):
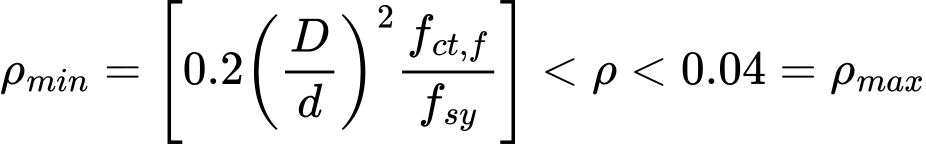
![]()
If the maximum degree of total reinforcement ρmax is exceeded, the program informs the user that the longitudinal reinforcement cannot be designed for a given cross section.
Design of Shear Reinforcement for Slabs
The program allows determination of the required amount of shear reinforcement form by stirrups and bends, respectively.
First, the program computes the ultimate shear strength in a given section – the shear force transmitted by concrete Vuc (Art. 8.2.4.1) and the maximum allowable shear force Vu,max (Art. 8.2.3.3).
![]()
![]()
where:
![]()
![]()
![]()
![]()
![]()
![]()
As for stirrups the necessary reinforcement area is given by (Art. 8.2.5.2):
![]()
As for bends the necessary reinforcement area is given by (Art. 8.2.5.2):
![]()
SNiP 52-101-2003
This help contains the following computationals methods:
![]() Materials, coefficients, notation
Materials, coefficients, notation
![]() Verification of rectangular cross-section made of plain concrete
Verification of rectangular cross-section made of plain concrete
![]() Verification of rectangular RC cross-section
Verification of rectangular RC cross-section
![]() Verification of circular RC cross-section
Verification of circular RC cross-section
![]() Verification of spread footing for punching shear
Verification of spread footing for punching shear
![]() Design of longitudinal reinforcement for slabs
Design of longitudinal reinforcement for slabs
![]() Design of shear reinforcement for slabs
Design of shear reinforcement for slabs
Materials, Coefficients, Notation
The following notation for material parameters is used:
| Rb | – | design compressive strength of concrete |
| Rbt | – | design tensile strength of concrete |
| Rsc | – | design compressive strength of steel |
| Rs | – | design tensile strength of steel bar |
The most common notation for geometrical parameters:
| b | – | cross section width |
| h | – | cross section depth |
| h0 | – | effective depth of cross section |
| z | – | lever arm (arm of internal forces) |
Verification of Rectangular Cross-Section Made of Plain Concrete
The cross-section is rectangular, loaded by the bending moment M, normal force N (applied in the cross-section centroid) and by the shear force Q. The cross-section bearing capacity subjected to bending moment is given by:
![]()
The shear strength is provided by:
![]()
Strength of concrete cross-section subject to the combination of bending moment and normal force is derived from the following expressions depending on the normal force eccentricity e:
for:
![]()
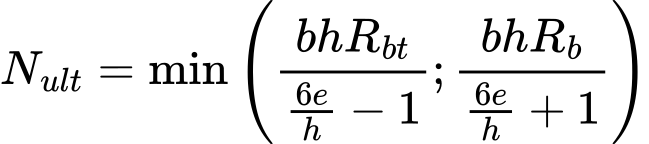
![]()
![]()
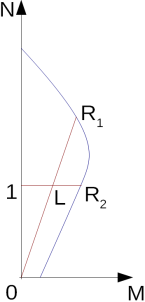 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R1| or |1L| / |1R2|. Where L is load, R1 is strength with prescribed eccentricity and R2 is strength with prescribed normal force.
Verification of Rectangular RC Cross-Section
The cross-section is rectangular, unilaterally reinforced and loaded by the bending moment and normal compression force. The program verifies a reinforced concrete section using the method of limit deformation. The maximum allowable strain of concrete in compression is 0.002 to 0.0035. Compression reinforcement is not taken into account.
The computed degree of reinforcement is checked using the following expressions:
![]()
![]()
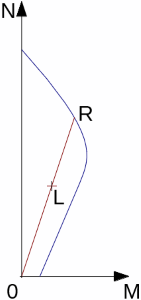 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed eccentricity.
Bending without normal force
The cross-section is rectangular, reinforced on one side and loaded by the bending moment M.
The ultimate moment is provided by:
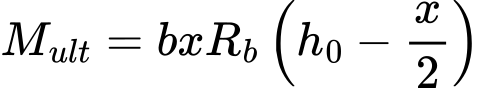
![]()
The program further checks whether the location of neutral axis x is less than the limit location of neutral axis xR given by:
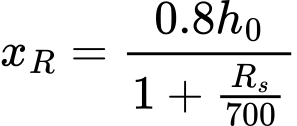
Shear
First, the program computes the ultimate shear strength of concrete Qb.
![]()
If the ultimate shear strength of concrete is exceeded, the ultimate shear strength Qmax is checked.
![]()
Next, the necessary reinforcement area is given by:
![]()
where:
![]()
Verification of Circular RC Cross-Section
The program verifies a reinforced concrete pile using the method of limit deformation. The maximum allowable strain of concrete in compression is 0.0015 – 0.0035. The degree of reinforcement is checked using the formula:
![]() Column – check for dominant compression
Column – check for dominant compression
![]()
![]()
![]() Beam – check for dominant bending
Beam – check for dominant bending
![]()
![]()
| where: | d | – | pile diameter |
| As | – | reinforcement area |
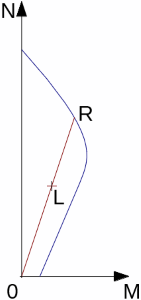 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed eccentricity.
Verification of Spread Footing for Punching Shear
The program allows to verify spread footing for punching shear or for the design of shear reinforcement. The critical section loaded in shear Ucr is distant from the column edge by one half of the footing thickness. It is loaded by the prescribed moments Mx, My and by the shear force F provided by:
![]()
| where: | A | – | area of footing |
| Q | – | assigned vertical force developed in column | |
| At | – | hatched area in fig. |
 Dimensioning of shear reinforcement area At
Dimensioning of shear reinforcement area At
The program computes the maximal shear force F developed in the critical section, the shear force transmitted by concrete with no shear reinforcement Fb,ult, and the maximal allowable force Fult,max:
![]()
![]()
For F< Fb,ult no shear reinforcement is needed.
For F > Fb,ult and F < Fult,max the shear reinforcement must be introduced. The ultimate shear force is given by:
![]()
![]()
| where: | Vcr | – | critical cross-section span |
| α | – | is angle of bends | |
| As | – | overall area of bends in footing |
For F> Fult,max the shear reinforcement cannot be designed. It is therefore necessary to increase the cross-section height.
Design of Longitudinal Reinforcement for Slabs
The design of reinforcement is performed for load caused by the bending moment M. The program provides the required area of tensile and compressive (if needed) reinforcement. It takes into account conditions for the minimum and maximum degree of reinforcement in a given cross-section. First, the program determines the location of neutral axis as:
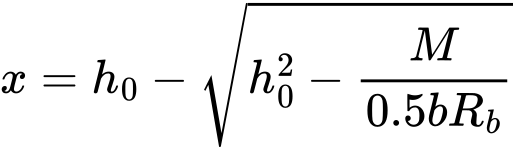
Providing the location of neutral axis is less than the allowable one (x < xmax), the program determines the area of tensile reinforcement Ast from the expression:
![]()
Providing the location of neutral axis is greater than the allowable one (x > xmax), the program determines the areas of both compressive Asc and tensile Ast reinforcement from the expressions:
![]()
![]()
![]()
The limit location of neutral axis is found from:
![]()
The computed degree of reinforcement is checked using the following expressions:
![]()
![]()
Design of Shear Reinforcement for Slabs
The program allows determination of the required amount of shear reinforcement form by stirrups and bends, respectively.
First, the program computes the ultimate shear strength in a given section – the shear force transmitted by concrete Qb and the maximum allowable shear force Qmax.
![]()
![]()
As for stirrups the necessary reinforcement area is given by:
![]()
As for bends the necessary reinforcement area is given by:
![]()
where:
![]()
GB 50010-2010
This help contains the following computationals methods:
![]() Materials, coefficients, notation
Materials, coefficients, notation
![]() Verification of rectangular cross-section made of plain concrete
Verification of rectangular cross-section made of plain concrete
![]() Verification of rectangular RC cross-section
Verification of rectangular RC cross-section
![]() Verification of circular RC cross-section
Verification of circular RC cross-section
![]() Verification of spread footing for punching shear
Verification of spread footing for punching shear
![]() Design of longitudinal reinforcement for slabs
Design of longitudinal reinforcement for slabs
![]() Design of shear reinforcement for slabs
Design of shear reinforcement for slabs
Materials, Coefficients, Notation
The following notation for material parameters is used:
| Rb | – | design compressive strength of concrete |
| Rbt | – | design tensile strength of concrete |
| Rsc | – | design compressive strength of steel |
| Rs | – | design tensile strength of steel bar |
The most common notation for geometrical parameters:
| b | – | cross section width |
| h | – | cross section depth |
| h0 | – | effective depth of cross section |
| z | – | lever arm (arm of internal forces) |
Verification of Rectangular Cross-Section Made of Plain Concrete
The cross-section is rectangular, loaded by the bending moment M, normal force N (applied in the cross-section centroid) and by the shear force Q. The cross-section bearing capacity subjected to bending moment is given by:
![]()
The shear strength is provided by:
![]()
Strength of concrete cross-section subject to the combination of bending moment and normal force is derived from the following expressions depending on the normal force eccentricity e:
for:
![]()
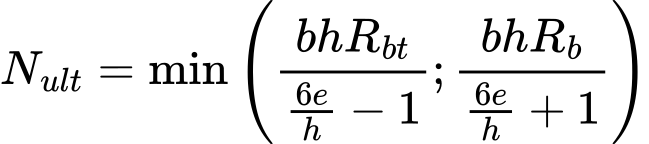
![]()
![]()
 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R1| or |1L| / |1R2|. Where L is load, R1 is strength with prescribed eccentricity and R2 is strength with prescribed normal force.
Verification of Rectangular RC Cross-Section
The cross-section is rectangular, unilaterally reinforced and loaded by the bending moment and normal compression force. The program verifies a reinforced concrete section using the method of limit deformation. The maximum allowable strain of concrete in compression is 0.002 to 0.0035. Compression reinforcement is not taken into account.
The computed degree of reinforcement is checked using the following expressions:
![]()
![]()
 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed eccentricity.
Bending without normal force
The cross-section is rectangular, reinforced on one side and loaded by the bending moment M.
The ultimate moment is provided by:
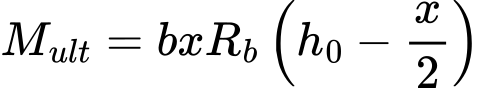
![]()
The program further checks whether the location of neutral axis x is less than the limit location of neutral axis xR given by:
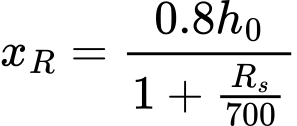
Shear
First, the program computes the ultimate shear strength of concrete Qb.
![]()
If the ultimate shear strength of concrete is exceeded, the ultimate shear strength Qmax is checked.
![]()
Next, the necessary reinforcement area is given by:
![]()
where:
![]()
Verification of Circular RC Cross-Section
The program verifies a reinforced concrete pile using the method of limit deformation. The maximum allowable strain of concrete in compression is 0.0015 – 0.0035. The degree of reinforcement is checked using the formula:
![]() Column – check for dominant compression
Column – check for dominant compression
![]()
![]()
![]() Beam – check for dominant bending
Beam – check for dominant bending
![]()
![]()
| where: | d | – | pile diameter |
| As | – | reinforcement area |
 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed eccentricity.
Verification of Spread Footing for Punching Shear
The program allows to verify spread footing for punching shear or for the design of shear reinforcement. The critical section loaded in shear Ucr is distant from the column edge by one half of the footing thickness. It is loaded by the prescribed moments Mx, My and by the shear force F provided by:
![]()
| where: | A | – | area of footing |
| Q | – | assigned vertical force developed in column | |
| At | – | hatched area in fig. |
 Dimensioning of shear reinforcement area At
Dimensioning of shear reinforcement area At
The program computes the maximal shear force F developed in the critical section, the shear force transmitted by concrete with no shear reinforcement Fb,ult, and the maximal allowable force Fult,max:
![]()
![]()
For F< Fb,ult no shear reinforcement is needed.
For F > Fb,ult and F < Fult,max the shear reinforcement must be introduced. The ultimate shear force is given by:
![]()
![]()
| where: | Vcr | – | critical cross-section span |
| α | – | is angle of bends | |
| As | – | overall area of bends in footing |
For F> Fult,max the shear reinforcement cannot be designed. It is therefore necessary to increase the cross-section height.
Design of Longitudinal Reinforcement for Slabs
The design of reinforcement is performed for load caused by the bending moment M. The program provides the required area of tensile and compressive (if needed) reinforcement. It takes into account conditions for the minimum and maximum degree of reinforcement in a given cross-section. First, the program determines the location of neutral axis as:
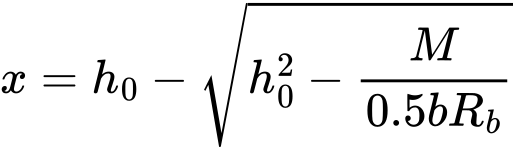
Providing the location of neutral axis is less than the allowable one (x < xmax), the program determines the area of tensile reinforcement Ast from the expression:
![]()
Providing the location of neutral axis is greater than the allowable one (x > xmax), the program determines the areas of both compressive Asc and tensile Ast reinforcement from the expressions:
![]()
![]()
![]()
The limit location of neutral axis is found from:
![]()
The computed degree of reinforcement is checked using the following expressions:
![]()
![]()
Design of Shear Reinforcement for Slabs
The program allows determination of the required amount of shear reinforcement form by stirrups and bends, respectively.
First, the program computes the ultimate shear strength in a given section – the shear force transmitted by concrete Qb and the maximum allowable shear force Qmax.
![]()
![]()
As for stirrups the necessary reinforcement area is given by:
![]()
As for bends the necessary reinforcement area is given by:
![]()
where:
![]()
NZS 3101-2006
This help contains the following computationals methods:
![]() Materials, coefficients, notation
Materials, coefficients, notation
![]() Verification of rectangular cross-section made of plain concrete
Verification of rectangular cross-section made of plain concrete
![]() Verification of rectangular RC cross-section
Verification of rectangular RC cross-section
![]() Verification of circular RC cross-section
Verification of circular RC cross-section
![]() Verification of spread footing for punching shear
Verification of spread footing for punching shear
![]() Design of longitudinal reinforcement for slabs
Design of longitudinal reinforcement for slabs
![]() Design of shear reinforcement for slabs
Design of shear reinforcement for slabs
Materials, Coefficients, Notation
The following notation for material parameters is used:
| Rb | – | design compressive strength of concrete |
| Rbt | – | design tensile strength of concrete |
| Rsc | – | design compressive strength of steel |
| Rs | – | design tensile strength of steel bar |
The most common notation for geometrical parameters:
| b | – | cross section width |
| h | – | cross section depth |
| h0 | – | effective depth of cross section |
| z | – | lever arm (arm of internal forces) |
Verification of Rectangular Cross-Section Made of Plain Concrete
The cross-section is rectangular, loaded by the bending moment M, normal force N (applied in the cross-section centroid) and by the shear force Q. The cross-section bearing capacity subjected to bending moment is given by:
![]()
The shear strength is provided by:
![]()
Strength of concrete cross-section subject to the combination of bending moment and normal force is derived from the following expressions depending on the normal force eccentricity e:
for:
![]()
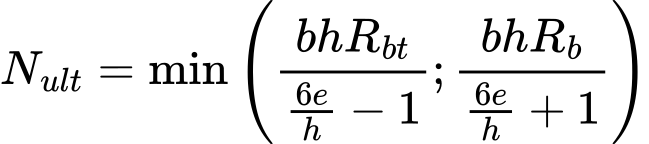
![]()
![]()
 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R1| or |1L| / |1R2|. Where L is load, R1 is strength with prescribed eccentricity and R2 is strength with prescribed normal force.
Verification of Rectangular RC Cross-Section
The cross-section is rectangular, unilaterally reinforced and loaded by the bending moment and normal compression force. The program verifies a reinforced concrete section using the method of limit deformation. The maximum allowable strain of concrete in compression is 0.002 to 0.0035. Compression reinforcement is not taken into account.
The computed degree of reinforcement is checked using the following expressions:
![]()
![]()
 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed eccentricity.
Bending without normal force
The cross-section is rectangular, reinforced on one side and loaded by the bending moment M.
The ultimate moment is provided by:
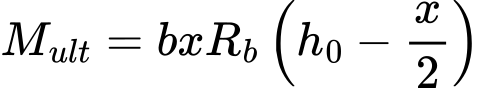
![]()
The program further checks whether the location of neutral axis x is less than the limit location of neutral axis xR given by:
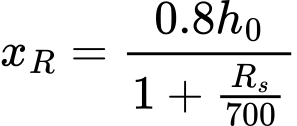
Shear
First, the program computes the ultimate shear strength of concrete Qb.
![]()
If the ultimate shear strength of concrete is exceeded, the ultimate shear strength Qmax is checked.
![]()
Next, the necessary reinforcement area is given by:
![]()
where:
![]()
Verification of Circular RC Cross-Section
The program verifies a reinforced concrete pile using the method of limit deformation. The maximum allowable strain of concrete in compression is 0.0015 – 0.0035. The degree of reinforcement is checked using the formula:
![]() Column – check for dominant compression
Column – check for dominant compression
![]()
![]()
![]() Beam – check for dominant bending
Beam – check for dominant bending
![]()
![]()
| where: | d | – | pile diameter |
| As | – | reinforcement area |
 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed eccentricity.
Verification of Spread Footing for Punching Shear
The program allows to verify spread footing for punching shear or for the design of shear reinforcement. The critical section loaded in shear Ucr is distant from the column edge by one half of the footing thickness. It is loaded by the prescribed moments Mx, My and by the shear force F provided by:
![]()
| where: | A | – | area of footing |
| Q | – | assigned vertical force developed in column | |
| At | – | hatched area in fig. |
 Dimensioning of shear reinforcement area At
Dimensioning of shear reinforcement area At
The program computes the maximal shear force F developed in the critical section, the shear force transmitted by concrete with no shear reinforcement Fb,ult, and the maximal allowable force Fult,max:
![]()
![]()
For F< Fb,ult no shear reinforcement is needed.
For F > Fb,ult and F < Fult,max the shear reinforcement must be introduced. The ultimate shear force is given by:
![]()
![]()
| where: | Vcr | – | critical cross-section span |
| α | – | is angle of bends | |
| As | – | overall area of bends in footing |
For F> Fult,max the shear reinforcement cannot be designed. It is therefore necessary to increase the cross-section height.
Design of Longitudinal Reinforcement for Slabs
The design of reinforcement is performed for load caused by the bending moment M. The program provides the required area of tensile and compressive (if needed) reinforcement. It takes into account conditions for the minimum and maximum degree of reinforcement in a given cross-section. First, the program determines the location of neutral axis as:
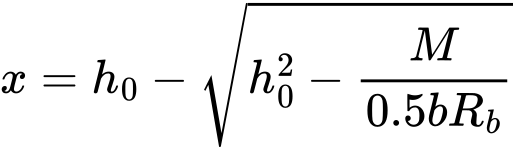
Providing the location of neutral axis is less than the allowable one (x < xmax), the program determines the area of tensile reinforcement Ast from the expression:
![]()
Providing the location of neutral axis is greater than the allowable one (x > xmax), the program determines the areas of both compressive Asc and tensile Ast reinforcement from the expressions:
![]()
![]()
![]()
The limit location of neutral axis is found from:
![]()
The computed degree of reinforcement is checked using the following expressions:
![]()
![]()
Design of Shear Reinforcement for Slabs
The program allows determination of the required amount of shear reinforcement form by stirrups and bends, respectively.
First, the program computes the ultimate shear strength in a given section – the shear force transmitted by concrete Qb and the maximum allowable shear force Qmax.
![]()
![]()
As for stirrups the necessary reinforcement area is given by:
![]()
As for bends the necessary reinforcement area is given by:
![]()
where:
![]()
CSA A23.3-14
This help contains the following computationals methods:
![]() Materials, coefficients, notation
Materials, coefficients, notation
![]() Verification of rectangular cross-section made of plain concrete
Verification of rectangular cross-section made of plain concrete
![]() Verification of rectangular RC cross-section
Verification of rectangular RC cross-section
![]() Verification of circular RC cross-section
Verification of circular RC cross-section
![]() Verification of spread footing for punching shear
Verification of spread footing for punching shear
![]() Design of longitudinal reinforcement for slabs
Design of longitudinal reinforcement for slabs
![]() Design of shear reinforcement for slabs
Design of shear reinforcement for slabs
Materials, Coefficients, Notation
The following notation for material parameters is used:
| Rb | – | design compressive strength of concrete |
| Rbt | – | design tensile strength of concrete |
| Rsc | – | design compressive strength of steel |
| Rs | – | design tensile strength of steel bar |
The most common notation for geometrical parameters:
| b | – | cross section width |
| h | – | cross section depth |
| h0 | – | effective depth of cross section |
| z | – | lever arm (arm of internal forces) |
Verification of Rectangular Cross-Section Made of Plain Concrete
The cross-section is rectangular, loaded by the bending moment M, normal force N (applied in the cross-section centroid) and by the shear force Q. The cross-section bearing capacity subjected to bending moment is given by:
![]()
The shear strength is provided by:
![]()
Strength of concrete cross-section subject to the combination of bending moment and normal force is derived from the following expressions depending on the normal force eccentricity e:
for:
![]()
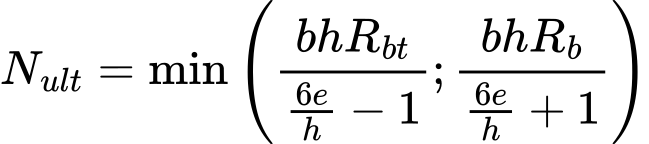
![]()
![]()
 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R1| or |1L| / |1R2|. Where L is load, R1 is strength with prescribed eccentricity and R2 is strength with prescribed normal force.
Verification of Rectangular RC Cross-Section
The cross-section is rectangular, unilaterally reinforced and loaded by the bending moment and normal compression force. The program verifies a reinforced concrete section using the method of limit deformation. The maximum allowable strain of concrete in compression is 0.002 to 0.0035. Compression reinforcement is not taken into account.
The computed degree of reinforcement is checked using the following expressions:
![]()
![]()
 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed eccentricity.
Bending without normal force
The cross-section is rectangular, reinforced on one side and loaded by the bending moment M.
The ultimate moment is provided by:
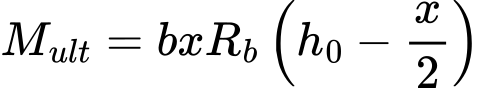
![]()
The program further checks whether the location of neutral axis x is less than the limit location of neutral axis xR given by:
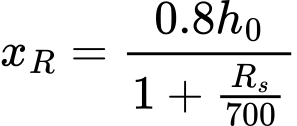
Shear
First, the program computes the ultimate shear strength of concrete Qb.
![]()
If the ultimate shear strength of concrete is exceeded, the ultimate shear strength Qmax is checked.
![]()
Next, the necessary reinforcement area is given by:
![]()
where:
![]()
Verification of Circular RC Cross-Section
The program verifies a reinforced concrete pile using the method of limit deformation. The maximum allowable strain of concrete in compression is 0.0015 – 0.0035. The degree of reinforcement is checked using the formula:
![]() Column – check for dominant compression
Column – check for dominant compression
![]()
![]()
![]() Beam – check for dominant bending
Beam – check for dominant bending
![]()
![]()
| where: | d | – | pile diameter |
| As | – | reinforcement area |
 Interaction diagram N-M
Interaction diagram N-M
Usage ratio of concrete cross-section subject to the combination of bending moment and normal force is determined as |0L| / |0R|. Where L is load and R is strength with prescribed eccentricity.
Verification of Spread Footing for Punching Shear
The program allows to verify spread footing for punching shear or for the design of shear reinforcement. The critical section loaded in shear Ucr is distant from the column edge by one half of the footing thickness. It is loaded by the prescribed moments Mx, My and by the shear force F provided by:
![]()
| where: | A | – | area of footing |
| Q | – | assigned vertical force developed in column | |
| At | – | hatched area in fig. |
 Dimensioning of shear reinforcement area At
Dimensioning of shear reinforcement area At
The program computes the maximal shear force F developed in the critical section, the shear force transmitted by concrete with no shear reinforcement Fb,ult, and the maximal allowable force Fult,max:
![]()
![]()
For F< Fb,ult no shear reinforcement is needed.
For F > Fb,ult and F < Fult,max the shear reinforcement must be introduced. The ultimate shear force is given by:
![]()
![]()
| where: | Vcr | – | critical cross-section span |
| α | – | is angle of bends | |
| As | – | overall area of bends in footing |
For F> Fult,max the shear reinforcement cannot be designed. It is therefore necessary to increase the cross-section height.
Design of Longitudinal Reinforcement for Slabs
The design of reinforcement is performed for load caused by the bending moment M. The program provides the required area of tensile and compressive (if needed) reinforcement. It takes into account conditions for the minimum and maximum degree of reinforcement in a given cross-section. First, the program determines the location of neutral axis as:
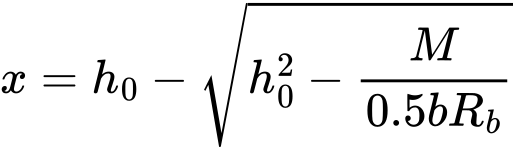
Providing the location of neutral axis is less than the allowable one (x < xmax), the program determines the area of tensile reinforcement Ast from the expression:
![]()
Providing the location of neutral axis is greater than the allowable one (x > xmax), the program determines the areas of both compressive Asc and tensile Ast reinforcement from the expressions:
![]()
![]()
![]()
The limit location of neutral axis is found from:
![]()
The computed degree of reinforcement is checked using the following expressions:
![]()
![]()
Design of Shear Reinforcement for Slabs
The program allows determination of the required amount of shear reinforcement form by stirrups and bends, respectively.
First, the program computes the ultimate shear strength in a given section – the shear force transmitted by concrete Qb and the maximum allowable shear force Qmax.
![]()
![]()
As for stirrups the necessary reinforcement area is given by:
![]()
As for bends the necessary reinforcement area is given by:
![]()
where:
![]()
EN 1992-1-1 (EC2) ou EN 1992-2
Esta ajuda contém os seguintes métodos:
![]() Materiais, coeficientes, notações
Materiais, coeficientes, notações
![]() Valores standard de coeficientes
Valores standard de coeficientes
![]() Verificação de secções transversais retangulares em concreto simples
Verificação de secções transversais retangulares em concreto simples
![]() Verificação de secções transversais retangulares em concreto armado
Verificação de secções transversais retangulares em concreto armado
![]() Verificação de secções transversais circulares em concreto armado
Verificação de secções transversais circulares em concreto armado
![]() Verificação de sapatas para o cisalhamento
Verificação de sapatas para o cisalhamento
![]() Dimensionamento de armaduras longitudinais para lajes
Dimensionamento de armaduras longitudinais para lajes
![]() Dimensionamento de armaduras de cisalhamento para lajes
Dimensionamento de armaduras de cisalhamento para lajes
![]() Verificação da dimensão de fendas
Verificação da dimensão de fendas
Materiais, Coeficientes, Notações
É utilizada a seguinte notação para os parâmetros materiais:
| fck | – | valor característico da resistência cilíndrica do concreto à compressão |
| fcd | – | resistência de dimensionamento do concreto à compressão |
| fcm | – | valor médio da resistência do concreto à compressão |
| fctm | valor médio da resistência do concreto à tração | |
| fctk0,05 | – | valor característico reduzido da resistência do concreto à tração |
| fctd | – | resistência de dimensionamento do concreto à tração |
| fyk | – | resistência característica do aço |
| fyd | – | resistência de dimensionamento do aço à tração |
A resistência característica do concreto à compressão é o parâmetro básico a introduzir dado pela classe do concreto – serve para derivar os restantes coeficientes (Tbl. 3.1).
| for: fck ≤ 50 Mpa | |
| for: fck > 50 Mpa | |
 | |
Os valores standard dos coeficientes αcc, γc, αct, γs estão integrados no programa – estes valores também podem ser introduzidos pelo usuário, consoante o Anexo Nacional selecionado.
podem
Notação mais comum para os parâmetros geométricos:
| b | – | largura da secção transversal |
| h | – | altura da secção transversal |
| d | – | altura efetiva da secção transversal |
| z | – | braço (braço das forças internas) |
Valores Standard de Coeficientes
Os programas contém um conjunto de coeficientes com valores padrão, que podem ser ajustados de acordo com os Anexos Nacionais. A tabela contém a descrição de cada coeficiente, o valor e o artigo correspondente da Norma que o apresenta. Em alguns casos, a equação que permite calcular a coeficiente contém uma variável que não apresenta nenhuma notação específica nos programas – nestes casos, esta variável aparece na expressão como X.
| Coeficiente | Valor | Notações | Artigo |
| γc | 1,5 | 2.4.2.4 | |
| γs | 1,15 | 2.4.2.4 | |
| αcc | 1 | 3.1.6 | |
| αct | 1 | 3.1.6 | |
| αcc,pl | 0,8 | 12.3.1 | |
| αct,pl | 0,8 | 12.3.1 | |
| k | 1,5 | 12.6.3 | |
| ρmin | 0,0013 | 9.2.1.1 | |
| X | 0,26 | 9.2.1.1 | |
| ρmax | 0,04 | 9.2.1.1 | |
| ρmin | 0,002 | 9.5.2 | |
| X | 0,1 | 9.5.2 | |
| ρmax | 0,04 | 9.5.2 | |
| X | 0,18 | 6.2.2 | |
| νmin | – | 6.2.2 | |
| X | 0,5 | 6.2.2 | |
| ν | – | 6.2.2 | |
| cot θmin | 1 | 6.2.3 | |
| cot θmax | 2,5 | 6.2.3 |
Anexo Nacional da República Checa (CSN EN 1992-1-1 – 2010)
| Coeficiente | Valor | Notações | Artigo |
| αct,pl | 0,7 | 12.3.1 |
os outros valores são standard
Anexo Nacional da Eslováquia (STN EN 1992-1-1 – 2008)
todos os valores são standard
Anexo Nacional da Polónia (PN EN 1992-1-1 – 2008)
| Coeficiente | Valor | Notações | Artigo |
| γc | 1,4 | 2.4.2.4 | |
| cot θmax | 2,0 | 6.2.3 |
os outros valores são standard
Anexo Nacional da Noruega (NS EN 1992-1-1 – 2004)
| Coeficiente | Valor | Notações | Artigo |
| αcc | 0,85 | 3.1.6 | |
| αct | 0,85 | 3.1.6 |
os outros valores são standard
Anexo Nacional da Roménia (BDS EN 1992-1-1 – 2005)
todos os valores são standard
Anexo Nacional de Itália (UNI EN 1992-1-1 – 2005)
| Coeficiente | Valor | Notações | Artigo |
| αcc | 0,85 | 3.1.6 | |
| ν | 0,5 for ≤C70/85 | 6.2.2 |
os outros valores são standard
National Annex United Kingdom (BS EN 1992-1-1 – 2004)
| Coeficiente | Valor | Notações | Artigo |
| αcc | 0,85 | 3.1.6 | |
| αcc,pl | 0,6 | 12.3.1 | |
| αct,pl | 0,6 | 12.3.1 |
os outros valores são standard
EN 1992-2 – 2007
| Coeficiente | Valor | Notações | Artigo |
| αcc | 0,85 | 3.1.6 |
os outros valores são standard
Verificação de Secções Transversais Retangulares em Concreto Simples
A secção transversal é retangular, carregada pelo momento fletor MEd, pela força normal NEd (aplicada no centroide da secção transversal) e pela força de cisalhamento VEd. A resistência ao cisalhamento é dada por (Art. 12.6.3):
![]()
onde: Acc – área do concreto à compressão
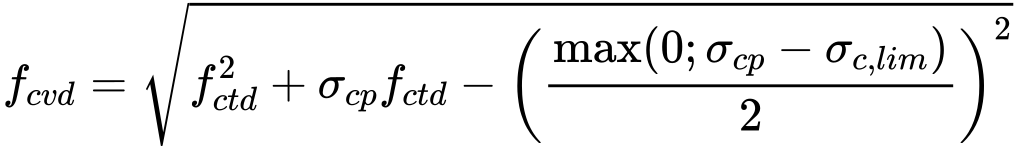
![]()
![]()
O valor standard do coeficiente k está inserido nos programas (Art. 12.6.3) – este valor também pode ser ajustado no programa, com base no Anexo Nacional selecionado.
A resistência da secção transversal em concreto está sujeita a uma combinação do momento fletor e da forçar normal, que é dada pelas expressões seguintes (Art. 12.6.1), com base na excentricidade da força normal e:
Como o máximo entre:
![]()
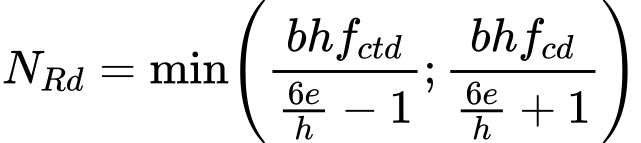
A fórmula permite definir a resistência a partir do diagrama tensão-deformação da secção transversal sem fendilhação.
![]()
![]()
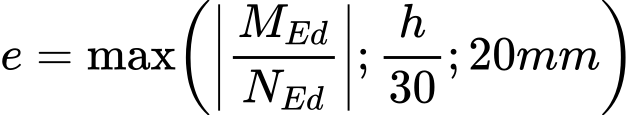
Os valores mínimos para a excentricidade estão presentes no artigo 6.1(3).
![]()
![]()
Os valores standard dos coeficientes αcc,pl, αct,pl, γc estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
 Diagrama de interação N-M
Diagrama de interação N-M
O rácio de utilização de concreto da secção transversal está sujeito à combinação do momento fletor com a força normal e é determinado como |0L| / |0R1| ou |1L| / |1R2|. Onde L é a carga, R1 é a resistência para uma certa excentricidade e R2 é a resistência para uma certa força normal.
Verificação de Secções Transversais Retangulares em Concreto Armado
A secção transversal é retangular, armada unilateralmente e carregada pela momento fletor e força normal de compressão. O programa verifica a secção de concreto armado através do método da deformação limite. A deformação máxima permitida para o concreto à compressão é 0,002 a 0,0035. Não é considerada armadura para a compressão. A excentricidade mínima é dada por (Art. 6.1(3)):
![]()
A quantidade de armadura computada é verificada de acordo com as expressões seguintes (Art. 9.2.1.1):
![]()
![]()
![]()
![]()
Os valores standard dos coeficientes ρmin, ρmax estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
 Diagrama de interação N-M
Diagrama de interação N-M
O rácio de utilização de concreto da secção transversal está sujeito à combinação do momento fletor com a força normal e é determinado como |0L| / |0R|. Onde L é a carga e R é a resistência para uma certa excentricidade.
Flexão sem força normal
A secção transversal é retangular, armada unilateralmente e carregada pelo momento fletor MEd.
O momento permitido para uma certa área de de armadura As é dado por (Art. 6.1, Art. 3.1.7(3)):
![]()
![]()
![]()
![]()
Os limites para a localização do eixo neutro são dados por (Art. 5.6.3(2)):
| xmax = 0,45d | para concreto C40/45 e inferior |
| xmax = 0,35d | para concreto C45/50 e superior |
Cisalhamento
Inicialmente, o programa computa a resistência ao cisalhamento última do concreto VRd,c (Art. 6.2.2(1)).
![]()
onde:
![]()
![]()
Se a resistência ao cisalhamento última do concreto for excedida, a resistência ao cisalhamento última VRd,max´ é assumida (Art. 6.2.3(3)):
![]()
Seguidamente, a área de armadura necessária é dada por (Art. 6.2.3(3)):
![]()
Os valores standard dos coeficientes ν, νmax, cot θmin, cot θmax estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
Verificação de Secções Transversais Circulares em Concreto Armado
O programa verifica uma estaca de concreto armado através do método da deformação limite. A deformação máxima permitida para o concreto à compressão é 0,002 – 0,0035. A resistência do concreto η*fcd é reduzida em dez por cento devido à forma da secção transversal (Art. 3.1.7).
A quantidade de armadura é verificada a partir da seguinte expressão:
![]()
![]() Estaca (Art. 9.8.5)
Estaca (Art. 9.8.5)
![]()
| Ac ≤ 0,5m2 | ρmin = 0,005 |
| 0,5m2 < Ac ≤ 1m2 | ρmin = 0,0025m2/Ac |
| Ac ≥ 1m2 | ρmin = 0,0025 |
| onde: | Ac | – | secção transversal da área da estaca |
![]()
![]() Pilar – verificação da compressão dominante (Art. 9.5.2)
Pilar – verificação da compressão dominante (Art. 9.5.2)
![]()
![]()
![]()
![]() Viga – verificação da flexão dominante (Art. 9.2.1.1)
Viga – verificação da flexão dominante (Art. 9.2.1.1)
![]()
![]()
![]()
| onde: | d | – | diâmetro da estaca |
| As | – | área armada da secção transversal |
Os valores standard dos coeficientes ρmin, ρmax estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
 Diagrama de interação N-M
Diagrama de interação N-M
O rácio de utilização de concreto da secção transversal está sujeito à combinação do momento fletor com a força normal e é determinado como |0L| / |0R|. Onde L é a carga e R é a resistência para uma certa excentricidade.
Cisalhamento
Inicialmente, o programa computa a resistência ao cisalhamento última do concreto VRd,c (Art. 6.2.2(1)). As fórmulas estão presentes no Art. 6.2.2(1), onde a largura da secção (bw) é substituída por 0,88d e a profundidade efetiva (d) é substituída por 0,8d.
![]()
onde:
![]()
![]()
Se a resistência ao cisalhamento última do concreto for excedida, a resistência ao cisalhamento última VRd,max e a resistência da secção armada VRd,s são verificadas (Art. 6.2.3(3)).
![]()
![]()
Os valores standard dos coeficientes ν, νmin, cot θmin, cot θmax estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
Verificação de Secções Transversais Circulares em Concreto Armado
O programa verifica uma estaca de concreto armado através do método da deformação limite. A deformação máxima permitida para o concreto à compressão é 0,002 – 0,0035. A resistência do concreto η*fcd é reduzida em dez por cento devido à forma da secção transversal (Art. 3.1.7).
A quantidade de armadura é verificada a partir da seguinte expressão:
![]()
![]() Estaca (Art. 9.8.5)
Estaca (Art. 9.8.5)
![]()
| Ac ≤ 0,5m2 | ρmin = 0,005 |
| 0,5m2 < Ac ≤ 1m2 | ρmin = 0,0025m2/Ac |
| Ac ≥ 1m2 | ρmin = 0,0025 |
| onde: | Ac | – | secção transversal da área da estaca |
![]()
![]() Pilar – verificação da compressão dominante (Art. 9.5.2)
Pilar – verificação da compressão dominante (Art. 9.5.2)
![]()
![]()
![]()
![]() Viga – verificação da flexão dominante (Art. 9.2.1.1)
Viga – verificação da flexão dominante (Art. 9.2.1.1)
![]()
![]()
![]()
| onde: | d | – | diâmetro da estaca |
| As | – | área armada da secção transversal |
Os valores standard dos coeficientes ρmin, ρmax estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
 Diagrama de interação N-M
Diagrama de interação N-M
O rácio de utilização de concreto da secção transversal está sujeito à combinação do momento fletor com a força normal e é determinado como |0L| / |0R|. Onde L é a carga e R é a resistência para uma certa excentricidade.
Cisalhamento
Inicialmente, o programa computa a resistência ao cisalhamento última do concreto VRd,c (Art. 6.2.2(1)). As fórmulas estão presentes no Art. 6.2.2(1), onde a largura da secção (bw) é substituída por 0,88d e a profundidade efetiva (d) é substituída por 0,8d.
![]()
onde:
![]()
![]()
Se a resistência ao cisalhamento última do concreto for excedida, a resistência ao cisalhamento última VRd,max e a resistência da secção armada VRd,s são verificadas (Art. 6.2.3(3)).
![]()
![]()
Os valores standard dos coeficientes ν, νmin, cot θmin, cot θmax estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
Verificação de Sapatas para o Cisalhamento
As sapatas são carregadas pelos momentos MEx, MEy e pela força de cisalhamento VE, de acordo com:
![]()
| onde: | A | – | área da sapata |
| V | – | força vertical desenvolvida no pilar atribuída | |
| At | – | área hachurada da fig. |
 Dimensionamento da área de armadura para o cisalhamento At
Dimensionamento da área de armadura para o cisalhamento At
O programa simula secções de controlo à distância de 0,5d a 2d, no caso de sapatas sem armadura para cisalhamento. No caso de sapatas reforçadas, as distâncias são de 0,5d a 4d, onde d é a profundidade efetiva da sapata. A armadura para cisalhamento é considerada nas secções de controlo, que estão a uma distância inferior a 2d do pilar. As secções de controlo são consideradas em intervalos de 0,25d.
A tensão do carregamento VEd em cada secção de controlo é obtida através de 6.4.3 (3),
![]()
![]()
![]()
a resistência ao punçoamento da sapata sem armadura para o cisalhamento VRd,c é obtida através de 6.4.4 (2)
![]()
![]()
![]()
e, se necessário, a resistência ao punçoamento para sapatas armadas VRd,cs é obtida através de 6.4.5 (1).
![]()
![]()
A resistência à compressão no centro do pilar VRd,max é calculada de acordo com 6.4.5 (3). VRd,max depende das dimensões do pilar e da espessura da sapata.
![]()
Para vEd < vRd,c, não é necessária armadura para cisalhamento.
Para vEd > vRd,c e vEd < vRd,max, deve ser introduzida armadura para cisalhamento
Para vEd > vRd,max, a resistência para o cisalhamento não pode ser dimensionada. É necessário aumentar a altura da secção transversal.
A secção de controlo com o pior rácio de carregamento e resistência é considerada como a crítica e assinalada pelo programa.
Os valores standard dos coeficientes ν, νmin estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
Dimensionamento de Armaduras Longitudinais para Lajes
O dimensionamento de armaduras é realizado para cargas devido a momentos fletores MEd. O programa fornece a área necessária para armaduras de tração e compressão (se necessário). São consideradas as condições para as quantidades de armadura máximas e mínimas para a secção transversal em análise. O programa começa por determinar a localização do eixo neutro conforme o descrito em (Art. 3.1.7, Art. 6.1):
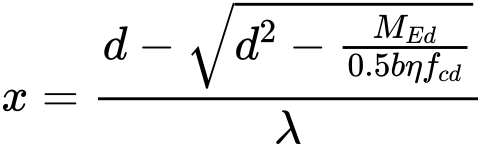
Se a localização do eixo neutro for inferior ao permitido (x < xmax), o programa determina a área da armadura de tração Ast a partir da expressão:
![]()
Se a localização do eixo neutro for superior ao permitido (x > xmax), o programa determina a área das armaduras de compressão Asc e de tração Ast a partir das expressões:
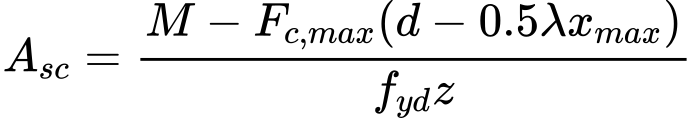
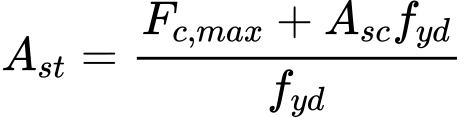
![]()
Os limites para a localização do eixo neutro são dados por (Art. 5.6.3(2)):
| xmax = 0,45d | para concreto C40/45 e inferior |
| xmax = 0,35d | para concreto C45/50 e superior |
A quantidade de armadura computada é verificada através das expressões seguintes (Art. 9.3.1.1):
![]()
![]()
![]()
Os valores standard dos coeficientes ρmin, ρmax estão inseridos nos programas – estes valores também podem ser ajustados, com base no Anexo Nacional selecionado.
Se a quantidade máxima de armadura total ρmax for excedida, o programa informa o usuário que a armadura longitudinal não pode ser dimensionada para a secção transversal em análise.
Dimensionamento de Armaduras de Cisalhamento para Lajes
O programa permite determinar a quantidade necessária de armadura para o cisalhamento a partir de estribos e tirantes curvos.
O programa começa por computar a resistência ao cisalhamento última de uma dada secção – a força de cisalhamento transmitida pelo concreto VRd1 (Art. 17.4.2.2 – Modelo I ) e a força de cisalhamento máxima permitida VRd2 (Art. 17.4.2.2).
![]()
onde:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Para estribos, a área de armadura necessária é dada por (Art. 17.4.2.2):
![]()
Para tirantes curvos, a área de armadura necessária é dada por (Art. 17.4.2.2):
![]()

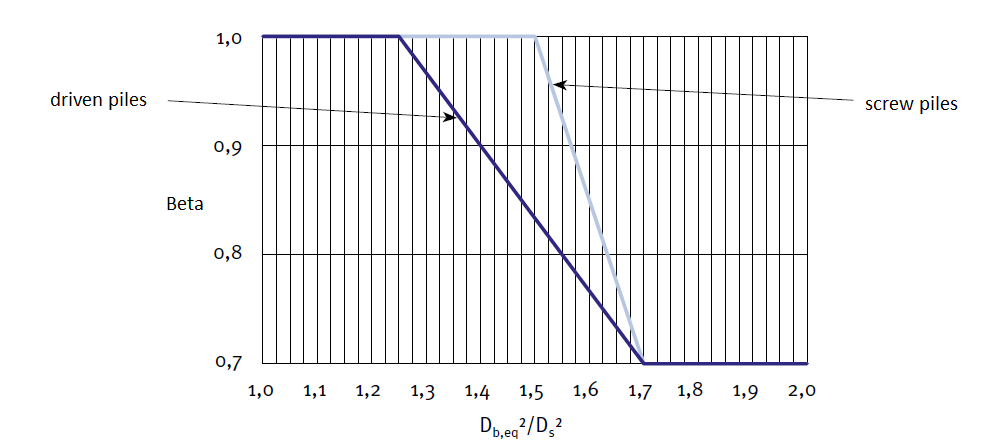

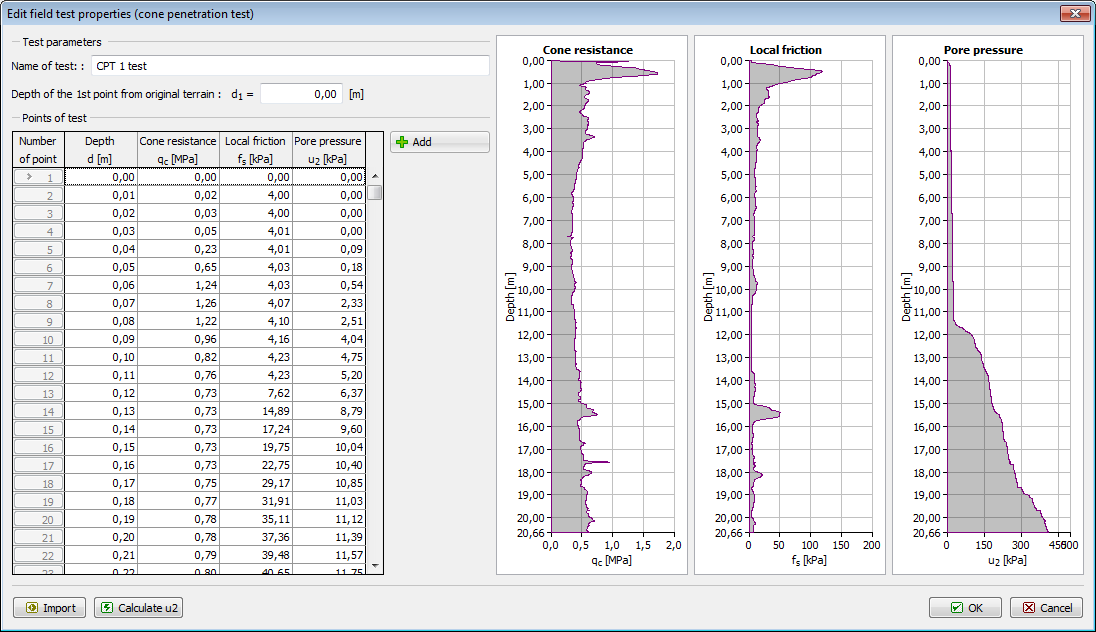
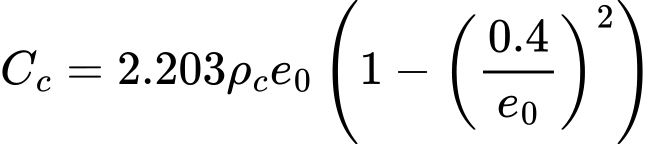
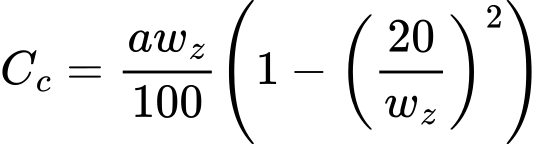
 Teste o software GEO5.
Teste o software GEO5.
